De Laplace

1 Enunciado

Un disco de radio R (sólido "0"), se mueve contenido siempre en el mismo plano vertical OXY. El centro C del disco realiza un movimiento rectilíneo uniforme con velocidad v₀ respecto del plano horizontal fijo (sólido "1"), sobre el que rueda sin deslizar. Un barra rígida de longitud 4R (sólido "2"), contenida también en OXYZ, tiene su extremo A articulado en un punto del perímetro del disco, mientras que su extremo B se desliza sobre el plano horizontal.

1. Determina la posición de los C.I.R. en las cuatro posiciones indicadas en la figura.
2. Explica qué tipo de movimiento realiza la barra en cada uno de los instantes correspondientes a dichas posiciones.

2 Solución

2.1 Solución gráfica

La imagen muestra la resolución gráfica de la cuestión. El disco rueda sin deslizar, por lo que el C.I.R. correspondiente al movimiento "01" es siempre el punto de contacto del disco con el suelo. Por otro lado, el punto A donde la barra está articulada al disco pertenece siempre a los dos sólidos a la vez, es decir, 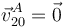. Por tanto, el punto A es el C.I.R. del movimiento "20", 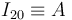. Según el teorema de los tres centros, el punto I₂₁ debe situarse sobre la línea que une los puntos I₂₀ y I₀₁.

Por otro lado, el punto B de la barra sólo puede moverse deslizando sobre el suelo (sólido "1"). Por tanto su velocidad sólo puede tener componente horizontal. Como es un movimiento plano, el C.I.R. I₂₁ debe estar situado sobre la línea perpendicular a y que pasa por el punto B, como se indica en la figura.

Ahora podemos analizar cada uno de los casos e identificar el tipo de movimiento instantáneo de la barra.

2.2 Caso 1

El punto I₂₁ se encuentra en la intersección de las rectas 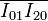y la recta perpendicular a que pasa por B. Como estas dos rectas son paralelas su intersección ocurre en el infinito. Por tanto, I₂₁ está en el infinito (hacia arriba o hacia abajo) y en ese instante el movimiento "21" es una traslación instantánea.

2.3 Caso 2

Ahora la recta 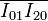corta a la recta perpendicular a en un punto, que es el I₂₁. En este instante el movimiento "21" es una rotación instantánea.

2.4 Caso 3

Ahora I₂₀ y I₀₁ coinciden en el punto A. Por tanto todas las velocidades en A se anulan, en particular 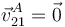. La condición cinemática de sólido rígido aplicada a la barra es

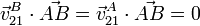
Ahora bien, sólo puede tener componente horizontal, en este caso, debe ser paralela a la barra. Por tanto

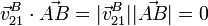
Como 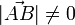tenemos que 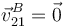y por tanto 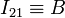. Es decir, la barra está en reposo instantáneo.

Otra forma de ver que 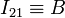es observar que al pasar del caso 1 al 2 y luego al 3 el C.I.R. I₂₁ se mueve a lo largo de la recta perpendicular a que pasa por B.

2.5 Caso 4

La situación es similar a la del caso 2, sólo que esta vez el punto I₂₁ está por debajo del suelo. El movimiento es una rotación instantánea.