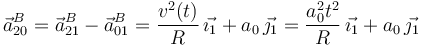Placa empujando un disco (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

El cuadrado de la figura (sólido "0") realiza un movimiento plano cuando uno de sus lados desliza sobre un plano horizontal fijo (sólido "1"). El cuadrado empuja a un disco de radio $R$ (sólido "2") que rueda sin deslizar sobre el plano "1".

Determine la posición de los C.I.R. de los diferentes movimientos en el instante reflejado en la figura.
Determine las reducciones cinemáticas de los movimientos en el instante en que la velocidad absoluta del punto $A$ del sólido "0" es $\vec{v}_{01}^A = v\vec{\imath_1}$ .
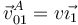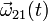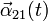Si el sistema parte del reposo y el punto $A$ del sólido "0" realiza un movimiento uniformemente acelerado, con aceleración $a 0$ , obtenga la expresión en función del tiempo del vector rotación $\vec{\omega}_{21}(t)$ y su derivada temporal $\vec{\alpha}_{21}(t)$ .
En las condiciones del apartado anterior, calcule la expresión de la aceleración 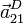$\vec{a}_{21}^D$ , así como la velocidad y aceleración relativa 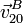$\vec{v}_{20}^B$ y $\vec{a}_{20}^B$ .

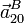2 Solución

2.1 Determinación gráfica de los C.I.R.

El disco desliza con una de sus caras siempre apoyada sobre el suelo. Por tanto el movimiento {01} es una traslación permanente. Esto quiere decir que $I 01$ está en el infinito en dirección perpendicular a la velocidad $\vec{v}_{01}$ , ya sea hacia arriba o hacia abajo.

Por otro lado, el disco "2" rueda sin deslizar sobre el suelo. Esto quiere decir que en el punto de contacto la velocidad relativa entre los dos sólidos es nula, 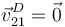$\vec{v}^D_{21}=\vec{0}$ y el C.I.R. del movimiento {21} está en el punto $D$ , es decir, 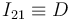$I_{21}\equiv D$ . La figura de la derecha muestra la localización de estos C.I.R.

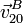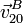El teorema de los tres centros nos dice que $I 20$ debe estar sobre la línea que une $I 21$ y $I 01$ , la línea vertical que se muestra en la figura. Por otro lado, podemos saber la dirección de la velocidad $\vec{v}^B_{20}$ . Al avanzar, el cuadrado empuja al disco hacia la derecha. Por tanto el punto $B$ debe desplazarse hacia arriba, esto es, $\vec{v}^B_{20}$ es paralela al eje $Y 1$ . El corte de la línea perpendicular a $\vec{v}^B_{21}$ trazada en $B$ con la línea que une $I 21$ y $I 01$ nos da la posición de $I 20$ . 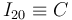Como vemos en la figura, $I_{20}\equiv C$ .

2.2 Reducciones cinemáticas de los movimientos

2.2.1 Movimiento {01}

Este es una traslación permanente. La velocidad angular es nula y la velocidad de todos los puntos de sólido "0" es la misma. El enunciado nos dice que 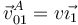$\vec{v}^A_{01}=v\vec{\imath_1}$ . Entonces la reducción es

$\vec{\omega}_{01}=\vec{0},\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}_{01}=v\vec{\imath_1}$

La velocidad no se adscribe a ningún punto concreto porque todos los puntos del sólido tienen la misma.

2.2.2 Movimiento {21}

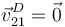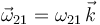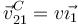El disco rueda sin deslizar sobre el punto $D$ . Entonces $\vec{v}^D_{21}=\vec{0}$ . El vector velocidad angular es de la forma $\vec{\omega}_{21}=\omega_{21}\,\vec{k}$ , pues es un movimiento plano. Para determinar el valor de $ω 21$ nos fijamos en que el punto $C$ del sólido "2" realiza una traslación permanente. Además su posición relativa respecto al punto $A$ no cambia. Por tanto $\vec{v}^C_{21}=v\vec{\imath_1}$ . Usando la ecuación del campo de velocidades del movimiento {21} tenemos

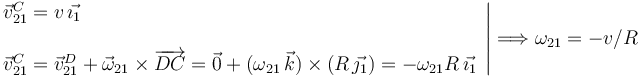
$\left. \begin{array}{l} \vec{v}^C_{21}=v\,\vec{\imath_1}\\ \\ \vec{v}^C_{21}=\vec{v}^D_{21}+\vec{\omega}_{21}\times\overrightarrow{DC}=\vec{0}+(\omega_{21}\,\vec{k})\times(R\,\vec{\jmath_1})= -\omega_{21}R\,\vec{\imath_1} \end{array} \right| \Longrightarrow \omega_{21}=-v/R$

Nos queda entonces que la reducción cinemática del movimiento {21} es

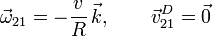
$\vec{\omega}_{21}=-\frac{v}{R}\,\vec{k},\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}^D_{21}=\vec{0}$

2.2.3 Movimiento {20}

Para reducir este movimiento usamos la composición de movimientos

{20} = {21} + {10}

Para la velocidad angular tenemos

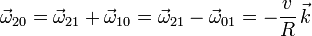
$\vec{\omega}_{20} = \vec{\omega}_{21} + \vec{\omega}_{10} = \vec{\omega}_{21} - \vec{\omega}_{01} = -\frac{v}{R}\,\vec{k}$

Obtenemos la velocidad de este movimiento en el punto $C$

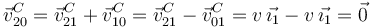
$\vec{v}^C_{20} = \vec{v}^C_{21} + \vec{v}^C_{10} = \vec{v}^C_{21} - \vec{v}^C_{01} = v\,\vec{\imath_1}-v\,\vec{\imath_1}=\vec{0}$

Así pues, la reducción queda

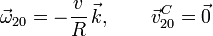
$\vec{\omega}_{20}=-\frac{v}{R}\,\vec{k},\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}^C_{20}=\vec{0}$

2.3 El cuadrado se desliza con aceleración uniforme

El movimiento {01} es una traslación, por lo que en cada instante de tiempo tenemos

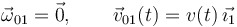
$\vec{\omega}_{01}=\vec{0},\,\,\,\,\,\,\,\,\,\,\,\,\vec{v}_{01}(t)=v(t)\,\vec{\imath_1}$

Al ser un movimiento uniformemente acelerado y partir del reposo, la velocidad $v (t)$ es

v (t) = a 0 t

Como hemos visto en el apartado anterior, la posición relativa del punto $C$ del sólido "2" respecto al cuadrado no cambia, por lo que en todo instante se cumple

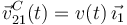
$\vec{v}^C_{21}(t) = v(t)\,\vec{\imath_1}$

En todo instante el disco rueda sin deslizar, por lo que si llamamos $D *$ al punto de contacto instantáneo del disco con el suelo, para cada instante de tiempo se cumple

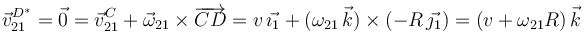
$\vec{v}^{D^*}_{21}=\vec{0} = \vec{v}^C_{21}+\vec{\omega}_{21}\times\overrightarrow{CD}= v\,\vec{\imath_1}+(\omega_{21}\,\vec{k})\times(-R\,\vec{\jmath_1})=(v+\omega_{21}R)\,\vec{k}$

Como esta relación se cumple para todo $t$ , obtenemos

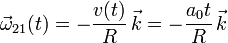
$\vec{\omega}_{21}(t) = -\frac{v(t)}{R}\,\vec{k}=-\frac{a_0t}{R}\,\vec{k}$

La aceleración angular 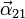$\vec{\alpha}_{21}$ se obtiene derivando respecto al tiempo

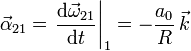
$\vec{\alpha}_{21} = \left.\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1 = -\frac{a_0}{R}\,\vec{k}$

2.4 Apartado 4

En el apartado anterior hemos visto que en todo instante 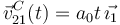$\vec{v}^C_{21}(t)=a_0t\,\vec{\imath_1}$ . Derivando respecto al tiempo obtenemos

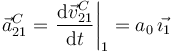
$\vec{a}^C_{21} = \left.\frac{\mathrm{d}\vec{v}^C_{21}}{\mathrm{d}t}\right|_1 = a_0\,\vec{\imath_1}$

Usando la ecuación del campo de aceleraciones del movimiento {21} tenemos, teniendo en cuenta que es un movimiento plano

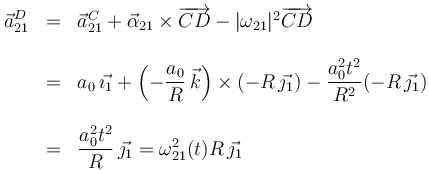
$\begin{array}{rcl} \displaystyle \vec{a}^D_{21}&=&\vec{a}^C_{21}+\vec{\alpha}_{21}\times\overrightarrow{CD}-|\omega_{21}|^2\overrightarrow{CD}\\ && \\ \displaystyle &=&\displaystyle a_0\,\vec{\imath_1} + \left(-\frac{a_0}{R}\,\vec{k}\right)\times(-R\,\vec{\jmath_1}) -\frac{a_0^2t^2}{R^2}(-R\,\vec{\jmath_1})\\ &&\\ &=&\displaystyle \frac{a_0^2t^2}{R}\,\vec{\jmath_1}=\omega^2_{21}(t)R\,\vec{\jmath_1} \end{array}$

Calculamos 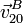$\vec{v}^B_{20}$ a partir de 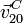$\vec{v}^C_{20}$ , la ecuación del campo de velocidades del movimiento {20} y la composición de movimientos {20} = {21} + {10}

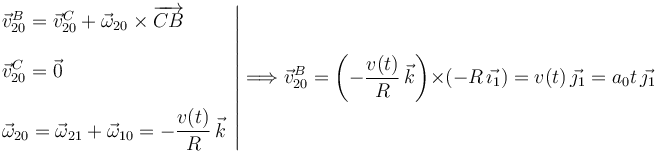
$\left. \begin{array}{l} \vec{v}^B_{20} = \vec{v}^C_{20}+\vec{\omega}_{20}\times\overrightarrow{CB}\\ \\ \displaystyle \vec{v}^C_{20}= \vec{0}\\ \\ \displaystyle \vec{\omega}_{20}=\vec{\omega}_{21}+\vec{\omega}_{10}=-\frac{v(t)}{R}\,\vec{k} \end{array} \right|\Longrightarrow \vec{v}^B_{20} = \left(-\frac{v(t)}{R}\,\vec{k}\right)\times(-R\,\vec{\imath_1})=v(t)\,\vec{\jmath_1}=a_0t\,\vec{\jmath_1}$

La ley de composición de velocidades angulares es válida para todo $t$ , por lo que puede usarse sin problemas.

Por último, calculamos $\vec{a}^B_{20}$ a partir de la composición de movimientos {21} = {20} + {01}

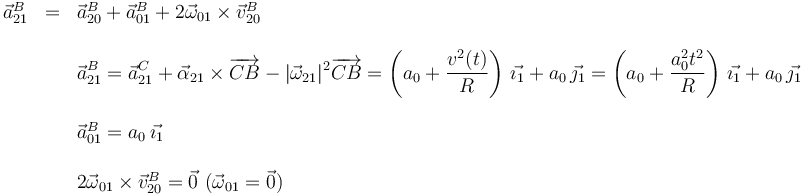
$\begin{array}{lcl} \vec{a}^B_{21}&=&\vec{a}^B_{20}+\vec{a}^B_{01} +2\vec{\omega}_{01}\times\vec{v}^B_{20}\\ \\ &&\displaystyle\vec{a}^B_{21} = \vec{a}^C_{21}+\vec{\alpha}_{21}\times\overrightarrow{CB}-|\vec{\omega}_{21}|^2\overrightarrow{CB}= \left(a_0+\frac{v^2(t)}{R}\right)\,\vec{\imath_1}+a_0\,\vec{\jmath_1}=\left(a_0+\frac{a_0^2t^2}{R}\right)\,\vec{\imath_1}+a_0\,\vec{\jmath_1}\\ && \\ &&\vec{a}^B_{01}=a_0\,\vec{\imath_1}\\ && \\ &&2\vec{\omega}_{01}\times\vec{v}^B_{20}=\vec{0} \,\, (\vec{\omega}_{01}=\vec{0}) \end{array}$

Despejando obtenemos

$\vec{a}^B_{20} = \vec{a}^B_{21}-\vec{a}^B_{01} = \frac{v^2(t)}{R}\,\vec{\imath_1}+a_0\,\vec{\jmath_1}=\frac{a_0^2t^2}{R}\,\vec{\imath_1}+a_0\,\vec{\jmath_1}$

Placa empujando un disco (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Determinación gráfica de los C.I.R.

2.2 Reducciones cinemáticas de los movimientos

2.2.1 Movimiento {01}

2.2.2 Movimiento {21}

2.2.3 Movimiento {20}

2.3 El cuadrado se desliza con aceleración uniforme

2.4 Apartado 4

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES