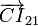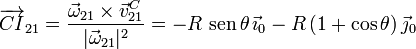Partícula moviéndose radialmente sobre el radio de un disco (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Vectores velocidad y aceleración del punto P en el movimiento {21}
- 2.2 CIR del movimiento {21}

1 Enunciado

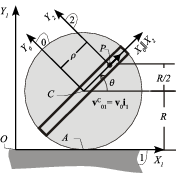
Una partícula $P$ recorre con velocidad constante $v 0$ el diámetro de un disco de radio $R$ (sólido "0"). A su vez, el disco, contenido en todo instante en el plano fijo $O X 1 Y 1$ (sólido "1") rueda sin deslizar sobre el eje $O X 1$ , de tal modo que su centro $C$ avanza con velocidad 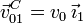$\vec{v}_{01}^C=v_0\,\vec{\imath}_1$ .

Asociando al disco el triedro solidario $C X 0 Y 0$ (sólido "0"), y definiendo un triedro auxilar $P X 2 Y 2$ (sólido "2") cuyos ejes $P X 2$ y $P Y 2$ tienen las mismas direcciones que los ejes $C X 0$ y $C Y 0$ , respectivamente; determina, en función de los datos del problema ( $R$ y $v 0$ ) y de las coordenadas polares que se definen en la figura ( $ρ$ y $θ$ ):

La velocidad absoluta ( 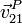$\vec{v}_{21}^P$ ) y la aceleración absoluta ( 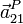$\vec{a}_{21}^P$ ) de la partícula $P$ .
La posición del C.I.R. del movimiento {21} (analíticamente).

"'Nota:"' Se recomienda el uso de la base vectorial asociada al triedro "0" para resolver el ejercicio.

2 Solución

2.1 Vectores velocidad y aceleración del punto P en el movimiento {21}

Vamos a analizar los movimientos {01} y {20}, y construiremos el {21} como combinación de estos dos.

2.1.1 Movimiento {01}

El disco rueda sin deslizar sobre el eje $O X 1$ , Por tanto el punto de contacto $A$ es el CIR. Por ahora, la reducción en $A$ es

$\vec{\omega}_{01}=\omega_{01}\,\vec{k}\qquad\qquad\vec{v}_{01}^A=\vec{0}$

Aún no conocemos el valor de la velocidad angular, que hay que poner en relación con los datos del problema. Para ello nos fijamos en que el enunciado nos da la velocidad 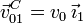$\vec{v}_{01}^C=v_0\,\vec{\imath}_1$ . Usando la ecuación del campo de velocidades, tenemos

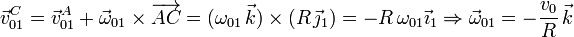
$\vec{v}_{01}^C=\vec{v}_{01}^A+\vec{\omega}_{01}\times\overrightarrow{AC}=(\omega_{01}\,\vec{k})\times(R\,\vec{\jmath}_1)= -R\,\omega_{01}\vec{\imath}_1\Rightarrow \vec{\omega}_{01}=-\dfrac{v_0}{R}\,\vec{k}$

La reducción en $C$ es

$\vec{\omega}_{01}=-\dfrac{v_0}{R}\,\vec{k}\qquad\qquad\vec{v}_{01}^C=v_0\,\vec{\imath}_1$

Necesitaremos más adelante el campo de aceleraciones. Podemos observar que la velocidad del punto $C$ es constante en este movimiento, y su expresión es siempre la dada por esta expresión. Además $\vec{\omega}_{01}$ también es constante en el tiempo. Entonces

$\vec{\alpha}_{01}=\vec{0}\qquad\qquad\vec{a}_{01}^C=\vec{0}$

Para calcular la aceleración del punto $P$ expresamos el vector 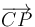$\overrightarrow{CP}$ en la base asociada al sólido "0". Obtenemos

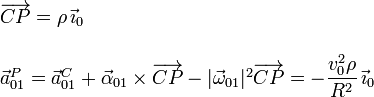
$\begin{array}{l} \overrightarrow{CP} = \rho\,\vec{\imath}_0\\ \\ \vec{a}_{01}^P = \vec{a}_{01}^C+\vec{\alpha}_{01}\times\overrightarrow{CP}-|\vec{\omega}_{01}|^2\overrightarrow{CP} = -\dfrac{v_0^2\rho}{R^2}\,\vec{\imath}_0 \end{array}$

2.1.2 Movimiento {20}

El punto $P$ describe una traslación sobre el diámetro del disco. En la figura hemos escogido el eje $C X 0$ coincidente con la trayectoria del punto sobre el disco. Al ser una traslación la velocidad angular es nula, y la velocidad es la misma en todos los puntos. La reducción en cualquier punto es

$\vec{\omega}_{20}=\vec{0}\qquad\qquad\vec{v}_{20}=v_0\vec{\imath}_0$

La aceleración angular es nula pues es una traslación en todo $t$ . Lo mismo ocurre con la aceleración lineal, pues la velocidad es constante. Entonces

$\vec{\alpha}_{20}=\vec{0}\qquad\qquad\vec{a}_{20}=\vec{0}$

En particular $\vec{a}_{20}^P=\vec{0}$ .

2.1.3 Movimiento {21}

Utilizando la composición {21}= {20} + {01} podemos escribir la reducción de este movimiento en el punto $C$

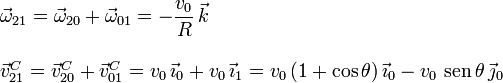
$\begin{array}{l} \vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}=-\dfrac{v_0}{R}\,\vec{k}\\ \\ \vec{v}_{21}^C=\vec{v}_{20}^C+\vec{v}_{01}^C = v_0\,\vec{\imath}_0+ v_0\,\vec{\imath}_1 = v_0\,(1+\cos\theta)\,\vec{\imath}_0-v_0\,\,\mathrm{sen}\,\theta\,\vec{\jmath}_0 \end{array}$

Hemos expresado el vector 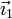$\vec{\imath}_1$ en la base asociada al triedro "0". Del dibujo tenemos

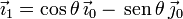
$\vec{\imath}_{1}=\cos\theta\,\vec{\imath}_0-\,\mathrm{sen}\,\theta\,\vec{\jmath}_0$

Se nos pide 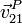$\vec{v}_{21}^P$ . Usando la ecuación del campo de velocidades del movimiento {21} tenemos

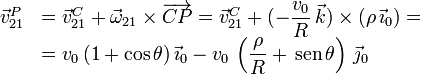
$\begin{array}{ll} \vec{v}_{21}^P&=\vec{v}_{21}^C+\vec{\omega}_{21}\times\overrightarrow{CP}= \vec{v}_{21}^C+(-\dfrac{v_0}{R}\,\vec{k})\times(\rho\,\vec{\imath}_0)=\\ &= v_0\,(1+\cos\theta)\,\vec{\imath}_0-v_0\,\left(\dfrac{\rho}{R}+\,\mathrm{sen}\,\theta\right)\,\vec{\jmath}_0 \end{array}$

Para hallar 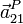$\vec{a}_{21}^P$ usamos la misma composición

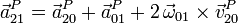
$\vec{a}_{21}^P=\vec{a}_{20}^P+\vec{a}_{01}^P+2\,\vec{\omega}_{01}\times\vec{v}_{20}^P$

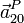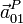Hemos calculado ya $\vec{a}_{20}^P$ y $\vec{a}_{01}^P$ . El término de Coriolis es

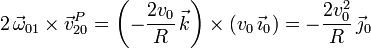
$2\,\vec{\omega}_{01}\times\vec{v}_{20}^P=\left(-\dfrac{2v_0}{R}\,\vec{k}\right)\times(v_0\,\vec{\imath}_0)= -\dfrac{2v_0^2}{R}\,\vec{\jmath}_0$

Con ello obtenemos

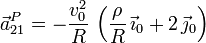
$\vec{a}_{21}^P = -\dfrac{v_0^2}{R}\,\left(\dfrac{\rho}{R}\,\vec{\imath}_0+2\,\vec{\jmath}_0\right)$

2.2 CIR del movimiento {21}

Como tenemos $\vec{\omega}_{21}$ y la velocidad en $C$ , podemos encontrar el vector $\overrightarrow{CI}_{21}$

$\overrightarrow{CI}_{21}=\dfrac{\vec{\omega}_{21}\times\vec{v}_{21}^C}{|\vec{\omega}_{21}|^2} = -R\,\,\mathrm{sen}\,\theta\,\vec{\imath}_0-R\,(1+\cos\theta)\,\vec{\jmath}_0$

Partícula moviéndose radialmente sobre el radio de un disco (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Vectores velocidad y aceleración del punto P en el movimiento {21}

2.1.1 Movimiento {01}

2.1.2 Movimiento {20}

2.1.3 Movimiento {21}

2.2 CIR del movimiento {21}

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES