Disco arrastrando una varilla

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

(Primer Parcial, Enero 2010, P1)

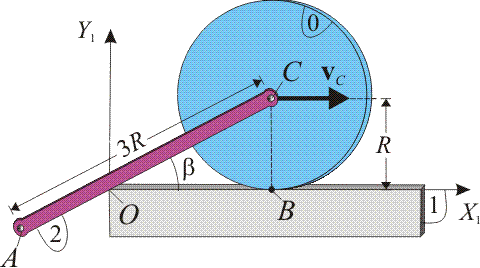
En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio

R

(sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco,

C

, se desplaza con una velocidad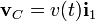 $\mathbf{v}_C=v(t)\mathbf{i}_1$ . La barra de longitud

3 R

(sólido “2”) tiene su extremo

C

articulado en el centro del disco, mientras que se apoya en el borde

O

del sólido “1”.

Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}.
En el instante en que la distancia entre los puntos $O$ y $B$ es igual a $R$ , la velocidad del punto $C$ es 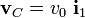$\mathbf{v}_C=v_0\ \mathbf{i}_1$ . Calcule las reducciones cinemáticas de los tres movimientos en el punto $C$ .
Exprese el vector de posición del punto $A$ en el sistema “1”, 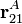$\mathbf{r}_{21}^A$ , en función de un ángulo $β$ arbitrario.
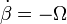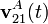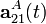Si $\dot{\beta}=-\Omega$ , con $Ω$ constante y positiva, calcule $\mathbf{v}_{21}^A(t)$ y $\mathbf{a}_{21}^A(t)$ para todo instante de tiempo, en función de $β$ , $Ω$ y $R$ .

2 Solución

Como paso previo a la solución de los distintos apartados procederemos a adoptar los sistemas de referencia equivalentes a los distintos sólidos rígidos del sistema bajo estudio. En la figura del enunciado se indican los ejes 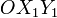$\displaystyle OX_1Y_1$ asocidados al sólido “1”, respecto del cuál, el disco “0” y la varilla “2” realizan sendos movimientos planos {01} y {21}, que tienen como plano director al definido por aquellos ejes; es decir, la dirección normal a dicho plano esta definida por el eje $O Z 1$ . Tal como se muestra en la figura, resulta conveniente adoptar sistemas de referencia ligados a los sólidos móviles “0” y “2” cuyas direcciones $C Z 0$ y $A Z 2$ sean también perpendiculares a dicho plano director. Tomando como eje $A X 2$ la dirección 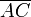$\overline{AC}$ definida por la varilla “2”, que forma un ángulo $β$ con el eje $O X 1$ , y como eje $C X 0$ una dirección arbitraria contenida en el disco “0”, se tendrá la siguiente relación entre los vectores de los triedros cartesianos asociados a cada uno de los sólidos:

$\begin{array}{l}\displaystyle \mathbf{i}_2=\cos\beta\ \mathbf{i}_1+\mathrm{sen} \beta\ \mathbf{j}_1 \\ \displaystyle \mathbf{j}_2=-\mathrm{sen} \beta\ \mathbf{i}_1+\cos\beta\ \mathbf{j}_1\\ \displaystyle \mathbf{k}_2=\mathbf{k}_1 \end{array}\qquad \qquad \qquad \qquad\begin{array}{l}\displaystyle \mathbf{i}_0=\cos\varphi\ \mathbf{i}_1-\mathrm{sen} \varphi\ \mathbf{j}_1 \\ \displaystyle \mathbf{j}_0=\mathrm{sen} \varphi\ \mathbf{i}_1+\cos\varphi\ \mathbf{j}_1\\ \displaystyle \mathbf{k}_0=\mathbf{k}_1 \end{array}$

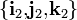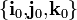Los movimientos relativos de los sólidos “2” y “0” respecto del sólido fijo “1” se corresponderán con sendas leyes horarias $β(t)$ y $\varphi(t)$ que describen cómo cambian en el tiempo dichos ángulos y, por tanto, cómo se mueven los triedros $\{\mathbf{i}_2\mathrm{,}\mathbf{j}_2\mathrm{,}\mathbf{k}_2\}$ y $\{\mathbf{i}_0\mathrm{,}\mathbf{j}_0\mathrm{,}\mathbf{k}_0\}$ , respecto del 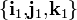$\{\mathbf{i}_1\mathrm{,}\mathbf{j}_1\mathrm{,}\mathbf{k}_1\}$ . Además, aplicando las fórmulas de Poisson podemos establecer la relación entre las derivadas de dichas leyes horarias y los vectores rotación instaneas de los movimientos {01} y {21}:

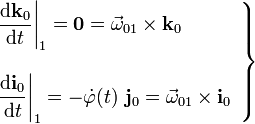
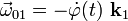
$\left.\begin{array}{l}\displaystyle \frac{\mathrm{d}\mathbf{k}_0}{\mathrm{d}t}\bigg|_1=\mathbf{0}=\vec{\omega}_{01}\times\mathbf{k}_0 \\ {} \\ \displaystyle \frac{\mathrm{d}\mathbf{i}_0}{\mathrm{d}t}\bigg|_1=-\dot{\varphi}(t)\ \mathbf{j}_0=\vec{\omega}_{01}\times\mathbf{i}_0\end{array}\right\}$ $\Rightarrow$ $\vec{\omega}_{01}=-\dot{\varphi}(t)\ \mathbf{k}_1$

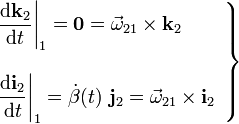
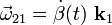
$\left.\begin{array}{l}\displaystyle \frac{\mathrm{d}\mathbf{k}_2}{\mathrm{d}t}\bigg|_1=\mathbf{0}=\vec{\omega}_{21}\times\mathbf{k}_2 \\{}\\ \displaystyle \frac{\mathrm{d}\mathbf{i}_2}{\mathrm{d}t}\bigg|_1=\dot{\beta}(t)\ \mathbf{j}_2=\vec{\omega}_{21}\times\mathbf{i}_2\end{array}\right\}$ $\Rightarrow$ $\vec{\omega}_{21}=\dot{\beta}(t)\ \mathbf{k}_1$

2.1 Determinación gráfica de los C.I.R.

Por tratarse de movimientos planos, los C.I.R. se corresponden con los puntos que en un determinado instante se encuentran en reposo (instantáneo o permanente). Consideremos el instante arbitrario $t$ , en que los ejes $A X 2$ y $C X 0$ forman sendos ángulos $β(t)$ y $\varphi (t)$ .

El sólido “0” (disco) rueda sin deslizar sobre el eje $O X 1$ ; por tanto, si $B$ es el punto de contacto entre ambos sólidos en el instante considerado, tendrá velocidad instantánea nula y sera el C.I.R. del movimiento {01}:

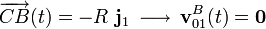
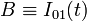
$\overrightarrow{CB}(t)=-R\ \mathbf{j}_1\, \longrightarrow\, \mathbf{v}_{01}^B(t)=\mathbf{0}$ $\Rightarrow$ $B\equiv I_{01}(t)$

En todo instante, el punto $C$ es el centro del disco “0” y uno de los extremos de la varilla “2”. Por tanto, se trata de un punto que permanece fijo en el movimiento relativo {20} (y también en el {02}). En consecuencia, el punto $C$ es el centro permanente de rotación de dicho(s) movimiento(s):

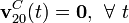
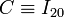
$\mathbf{v}_{20}^C(t)=\mathbf{0}\mathrm{,}\;\ \forall\ t$ $\Rightarrow$ $C\equiv I_{20}$

Además, utilizando la ley composición de velocidades instantáneas, se tendrá...

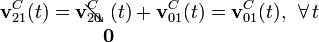
$\begin{array}{l}\displaystyle\mathbf{v}_{21}^C(t)=\mathbf{v}_{20}^C\!\!\!\!\!\!\!\searrow (t)+\mathbf{v}_{01}^C(t)=\mathbf{v}_{01}^C(t)\mathbf{,}\;\ \forall\, t\\ \qquad\qquad\quad\;\mathbf{0}\end{array}$

Aplicando el teorema de los tres centros se tendrán que el C.I.R. del movimiento {21}, en el instante considerado, debe encontrarse en la recta $\displaystyle\Delta$ determinada por los puntos $B$ y $C$ que, como hemos visto, se corresponden con los C.I.R. de los movimientos {01} y {20}, respectivamente. Por tanto,

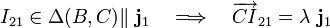
$I_{21}\in \Delta (B,C)\|\ \mathbf{j}_1\quad\Longrightarrow\quad\overrightarrow{CI}_{21}=\lambda\ \mathbf{j}_1$

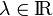siendo $\lambda\in \mathrm{I}\!\mathrm{R}$ el parámetro cuyo signo y valor determina la posición del $I 21$ respecto del punto $C$ en el instante considerado. Por otra parte, obsérvese que la recta $\displaystyle\Delta$ es la dirección contenida en el plano de movimiento que además es perpendicular a la velocidad del punto $C$ , tanto en el movimiento {01} como en el {21}. De esta forma, se tendrá...

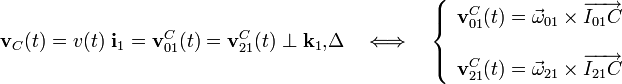
$\mathbf{v}_C(t)=v(t)\ \mathbf{i}_1=\mathbf{v}_{01}^C(t)=\mathbf{v}_{21}^C(t)\perp \mathbf{k}_1\mathbf{,}\Delta\quad\Longleftrightarrow\quad\left\{\begin{array}{l}\displaystyle\mathbf{v}_{01}^C(t)=\vec{\omega}_{01}\times\overrightarrow{I_{01}C}\\ \\ \displaystyle\mathbf{v}_{21}^C(t)=\vec{\omega}_{21}\times\overrightarrow{I_{21}C}\end{array}\right.$

Para determinar la posición del $I 21$ necesitamos conocer más datos, por ejemplo, la dirección de la velocidad de otro punto de la varilla en el movimiento {21}. Y este dato podemos conocerlo para el punto de dicho sólido “2” que en un determinado instante se halla en contacto con el vértice $O$ del sólido fijo “1”. Para verlo más claramente consideraremos el movimiento {12}; es decir, el que realiza el vértice $O$ del sólido “1” observado desde el sólido “2”: como dicho punto está siempre en contacto con la varilla, su velocidad en el movimiento {12} debe ser colineal con ella; es decir, tiene la dirección del segmento 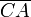$\overline{CA}$ . Y puesto que las velocidades instantáneas de un mismo punto en los movimientos {12} y {21} son opuestas, se verificará:

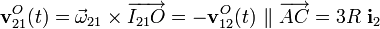
$\displaystyle\mathbf{v}_{21}^O(t)=\vec{\omega}_{21}\times\overrightarrow{I_{21}O}=-\mathbf{v}_{12}^O(t)\ \|\ \overrightarrow{AC}=3R\ \mathbf{i}_2$

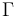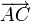Por tanto, el C.I.R. del movimiento {21}, $I 21$ , deber estar sobre la recta $\displaystyle\Gamma$ contenida en el plano de movimiento, que pasa por el punto $O$ y es perpendicular a la dirección definida por $\overrightarrow{AC}$ :

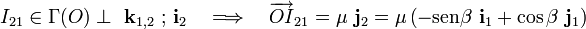
$I_{21}\in \Gamma (O)\perp \ \mathbf{k}_{1,2}\ \mathbf{;}\ \mathbf{i}_2\quad\Longrightarrow\quad\overrightarrow{OI}_{21}=\mu\ \mathbf{j}_2=\mu \left(-\mathrm{sen} \beta\ \mathbf{i}_1+\cos\beta\ \mathbf{j}_1\right)$

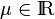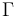donde $\mu\in \mathrm{I}\!\mathrm{R}$ es el parámetro cuyo signo y valor determina la posición del $I 21$ respecto de $O$ en el instante $t$ . La condición de pertenecia simultánea a las rectas $\displaystyle\Delta$ y $\displaystyle\Gamma$ permite determinar gráficamente la posición del C.I.R. del movimiento {21}:

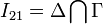
$I_{21}=\Delta\bigcap\Gamma$

Y con este resultado gráfico, ya es fácil determinar la posición relativa de dicho punto respecto de otros puntos de referencia del sistema y en función de sus propiedades geométricas. Consideremos los triángulos rectángulos $O B C$ y $O B I 21$ , ambos con su ángulo recto en sus correspondientes vértices $B$ . En el $O B C$ se verifica la relación,

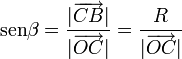
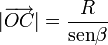
$\mathrm{sen}\beta=\frac{|\overrightarrow{CB}|}{|\overrightarrow{OC}|}=\frac{R}{|\overrightarrow{OC}|}$ $\Rightarrow$ $|\overrightarrow{OC}|=\frac{R}{\mathrm{sen}\beta}$

En el triángulo $O B I 21$ , el ángulo en el vértice $O$ es el complementario de $β$ , por lo que el del vértice correspondiente al $I 21$ es también el ángulo $β$ . Si se considera ahora un tercer triángulo rectángulo, el $C O I 21$ , con el ángulo recto en el vértice $O$ , se tendrá:

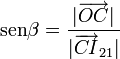
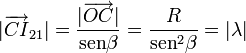
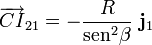
$\mathrm{sen}\beta=\frac{|\overrightarrow{OC}|}{|\overrightarrow{CI}_{21}|}$ $\Rightarrow$ $|\overrightarrow{CI}_{21}|=\frac{|\overrightarrow{OC}|}{\mathrm{sen}\beta}=\frac{R}{\mathrm{sen}^2\beta}=|\lambda|$ $\Rightarrow$ $\overrightarrow{CI}_{21}=-\frac{R}{\mathrm{sen}^2\beta}\ \mathbf{j}_1$

2.2 Reducciones cinemáticas en el punto $C$

En el enunciado se pide la expresión de las reducciones cinemáticas para los tres movimientos en el instante concreto $t 0$ , en el cual se verifica:

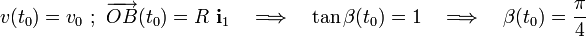
$v(t_0)=v_0\ \mathrm{;}\;\;\overrightarrow{OB}(t_0)=R\ \mathbf{i}_1\quad\Longrightarrow\quad\tan\beta(t_0)=1\quad\Longrightarrow\quad\beta(t_0)=\frac{\pi}{4}$

Pero a partir de los resultados del apartado anterior, es también inmediato obtener dichas reducciones en un instante arbitratio $t$ en el cuál el ángulo que forma la varilla con la horizontal es un valor arbitrario $β(t)$ , y la velocidad del centro del disco respecto del sólido “1” es 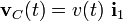$\mathbf{v}_C(t)=v(t)\ \mathbf{i}_1$ .

2.2.1 Reducción del movimiento {01}

Obtengamos el vector rotación instantánea y la velocidad del punto $C$ en dicho movimiento. El disco se mueve de manera que la velocidad de su centro viene dada por la expresión general 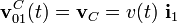$\mathbf{v}_{01}^C(t)=\mathbf{v}_C=v(t)\ \mathbf{i}_1$ . Además, hemos determinado que el punto de contacto $B$ es el C.I.R. de dicho movimiento, por lo que en todo instante debe verificarse...

$\displaystyle\mathbf{v}_{01}^C=\vec{\omega}_{01}\times\overrightarrow{BC}=\left[-\dot{\varphi}(t)\ \mathbf{k}_1\right]\times\left[R\ \mathbf{j}_1\right]= R\dot{\varphi}(t)\ \mathbf{i}_1=v(t)\ \mathbf{i}_1\quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle\mathbf{v}_{01}^C(t)=v(t)\ \mathbf{i}_1\\ \\ \displaystyle\vec{\omega}_{01}(t)=-\dot{\varphi}(t)\ \mathbf{k}_1=-\frac{v(t)}{R}\ \mathbf{k}_1\end{array}\right.$

La reducción cinemática en $t 0$ se obtiene particularizando el resultado anterior a dicho instante:

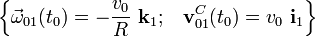
$\displaystyle\left\{\vec{\omega}_{01}(t_0)=-\frac{v_0}{R}\ \mathbf{k}_1\mathrm{;}\quad\mathbf{v}_{01}^C(t_0)=v_0\ \mathbf{i}_1\right\}$

2.2.2 Reducción del movimiento {21}

Puesto que el punto $C$ es también uno de los extremos de la varilla “2”, se cumplirá también 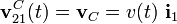$\mathbf{v}_{21}^C(t)=\mathbf{v}_C=v(t)\ \mathbf{i}_1$ . Y para relacionar esta velocidad con el vector rotación del movimiento {21}, utilizamos la expresión de la mposición del C.I.R. respecto del punto $C$ :

$\displaystyle\mathbf{v}_{21}^C=\vec{\omega}_{21}\times\overrightarrow{I_{21}C}=\left[\dot{\beta}(t)\ \mathbf{k}_1\right]\times\left[\frac{R\ }{\mathrm{sen}^2\beta(t)}\ \mathbf{j}_1\right]=-\frac{R\ \dot{\beta}(t)}{\mathrm{sen}^2\beta(t)}\ \mathbf{i}_1=v(t)\ \mathbf{i}_1 \quad\Longrightarrow\quad\left\{\begin{array}{l}\displaystyle\mathbf{v}_{21}^C(t)=v(t)\ \mathbf{i}_1\\ \\ \displaystyle\vec{\omega}_{21}(t)=\dot{\beta}(t)\ \mathbf{k}_1=-\frac{v(t)\ \mathrm{sen}^2\beta(t)}{R}\ \mathbf{k}_1\end{array}\right.$

... y sustituyendo los valores correspondientes a $t 0$ se obtiene la reducción en el instante solicitado:

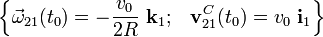
$\displaystyle\left\{\vec{\omega}_{21}(t_0)=-\frac{v_0}{2R}\ \mathbf{k}_1\mathrm{;}\quad\mathbf{v}_{21}^C(t_0)=v_0\ \mathbf{i}_1\right\}$

2.2.3 Reducción del movimiento {20}

Tanto para un instante genérico como para el $t 0$ , el vector rotación del movimiento {20} se puede obtener por la correspondiente ley de composición. En cuanto a la velocidad instantánea del punto $C$ en dicho movimiento, anteriormente establecimos que siempre va a ser nula:

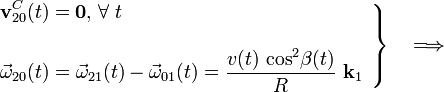
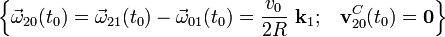
$\left.\begin{array}{l}\displaystyle\mathbf{v}_{20}^C(t)=\mathbf{0}\mathrm{,}\; \forall\ t\\ \\ \displaystyle\vec{\omega}_{20}(t)=\vec{\omega}_{21}(t)-\vec{\omega}_{01}(t)=\frac{v(t)\ \mathrm{cos}^2\beta(t)}{R}\ \mathbf{k}_1 \end{array}\right\}\quad\Longrightarrow$ $\displaystyle\left\{\vec{\omega}_{20}(t_0)=\vec{\omega}_{21}(t_0)-\vec{\omega}_{01}(t_0)=\frac{v_0}{2R}\ \mathbf{k}_1\mathrm{;}\quad\mathbf{v}_{20}^C(t_0)=\mathbf{0}\right\}$

Obsérvese que, con los datos proporcionados en este apartado, podemos conocer los vectores rotación y las velocidades instantáneas del punto $C$ , pero no podemos saber nada acerca de las aceleraciones instantáneas de dicho punto, ni sobre las derivadas de los vectores rotación. Para ello necesitaríamos conocer el valor de la derivada temporal 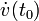$\dot{v}(t_0)$ .

2.3 Vector posición del punto $A$

El radio-vector 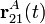$\mathbf{r}_{21}^A(t)$ expresa la posición del extremo $A$ de la varilla “2” respecto del punto fijo $O$ , en el transcurso del movimiento que se describe en el enunciado. Como la varilla siempre está en contacto con el punto $O$ , el segmento orientado $\overrightarrow{OA}$ tiene la misma dirección y sentido opuesto a 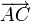$\overrightarrow{AC}$ ; es decir, va a ser colineal con el vector unitario 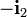$-\mathbf{i}_{2}$ . Por otra parte, su módulo ha de ser igual a la longitud total de la varilla ( $3 R$ ), menos la longitud del segmento comprendido entre el extremo $C$ y el punto de contacto con el sólido “1”, $O$ :

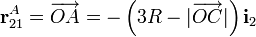
$\mathbf{r}_{21}^A=\overrightarrow{OA}=-\left(3R-|\overrightarrow{OC}|\right) \mathbf{i}_2$ $\Rightarrow$ $\displaystyle\mathbf{r}_{21}^A(t)= R\left(\frac{1}{\mathrm{sen}\beta(t)}-3\right)\left[\cos\beta(t)\ \mathbf{i}_1+\mathrm{sen} \beta(t)\ \mathbf{j}_1 \right]$

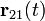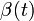Obsérvese que esta expresión proporciona las ecuaciones horarias $\mathbf{r}_{21} (t)$ que describen movimiento absoluto del punto $A$ , en términos de la ley horaria la ley horaria $\displaystyle \beta (t)$ .

2.4 Velocidad y aceleración de $A$

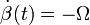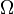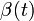En este último apartado se pide determinar cómo son la velocidad y aceleración instantánea de dicho extremo de la varilla, cuando ésta se mueve respecto del sólido “1” de manera que $\displaystyle\dot{\beta}(t)=-\Omega$ , siendo $\displaystyle \Omega$ una cantidad constante y positiva. A partir de este dato es muy fácil determinar la ley horaria $\displaystyle\beta(t)$ :

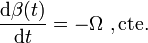
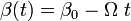
$\displaystyle\frac{\mathrm{d}\beta (t)}{\mathrm{d}t}=-\Omega\ \mathrm{, cte.}$ $\Rightarrow$ $\beta(t)=\beta_0-\Omega\ t$

siendo 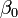$\displaystyle \beta_0$ el valor del ángulo formado por la varilla y la dirección horizontal $O X 1$ en el instante inicial $t = 0$ . Sustituyendo esta ley horaria en la última expresión del apartado anterior, obtendríamos las ecuaciones horarias del punto $A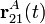$ , $\mathbf{r}_{21}^A(t)$ , cuando la varilla se mueve según las condiciones particulares expresadas en este apartado. Finalmente, sendas derivadas de primer y segundo orden con respecto al tiempo de estas ecuaciones horarias, proporcionan las expresiones de la velocidad y aceleración instantáneas de dicho extremo de la varilla:

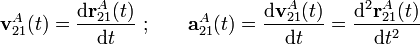
$\displaystyle\mathbf{v}_{21}^A(t)=\frac{\mathrm{d}\mathbf{r}_{21}^A(t)}{\mathrm{d}t}\ \mathrm{;}\qquad\displaystyle\mathbf{a}_{21}^A(t)=\frac{\mathrm{d}\mathbf{v}_{21}^A(t)}{\mathrm{d}t}=\frac{\mathrm{d}^2\mathbf{r}_{21}^A(t)}{\mathrm{d}t^2}$

Aunque conceptualmente simple, el procedimiento descrito puede resultar un poco complicado o farragoso en el cálculo. Esta dificultad puede evitarse parcialmente si, partiendo de la expresión general de la ley horaria, $\mathbf{r}_{21}^A[\beta(t)]$ , se aplica la regla de la cadena:

$\displaystyle\mathbf{v}_{21}^A(t)=\frac{\mathrm{d}\mathbf{r}_{21}^A}{\mathrm{d}\beta}\ \dot{\beta}=-\Omega\ \frac{\mathrm{d}\mathbf{r}_{21}^A}{\mathrm{d}\beta}=\mathbf{v}_{21}^A[\beta(t)]$

Obseérvese que esto proporcionaría una expresión de la velocidad instantánea del punto $A$ , en función de la posición del sistema en cada instante; es decir, en términos de la ley horaria 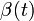$\displaystyle \beta(t)$ . Por tanto, la aceleración instantánea del punto puede determinarse de nuevo mediante la aplicación de la regla de la cadena:

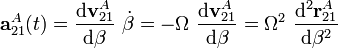
$\displaystyle\mathbf{a}_{21}^A(t)=\frac{\mathrm{d}\mathbf{v}_{21}^A}{\mathrm{d}\beta}\ \dot{\beta}=-\Omega\ \frac{\mathrm{d}\mathbf{v}_{21}^A}{\mathrm{d}\beta}=\Omega^2\ \frac{\mathrm{d}^2\mathbf{r}_{21}^A}{\mathrm{d}\beta^2}$

Como es evidente, este procedimiento no evita completamente los problemas asociados al cálculo de unas derivadas que, aún sin ser complicadas, sí pueden ser fuente de errores.

Sin embargo, existe otro procedimiento en el que, prácticamente, no es necesario realizar ninguna derivada: la aplicación de las propiedades del campo de velocidades y aceleraciones instantáneas para la varilla en el movimiento {21}:

2.4.1 Cálculo de la velocidad instantánea

A partir de la expresión general de la reducción cinemática obtenida en el apartado 2.2.2., se tendrá:

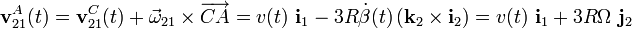
$\mathbf{v}_{21}^A(t)=\mathbf{v}_{21}^C(t)+\vec{\omega}_{21}\times\overrightarrow{CA}=v(t)\ \mathbf{i}_1-3R\dot{\beta}(t)\left(\mathbf{k}_2\times\mathbf{i}_2\right)=v(t)\ \mathbf{i}_1+3R\Omega\ \mathbf{j}_2$

Y teniendo en cuenta la relación general obtenida para la relación entre las componentes del vector rotación y de la velocidad instantánea del punto $C$ , se tendrá:

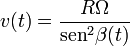
$v(t)=\frac{R\Omega}{\mathrm{sen}^2\beta(t)}$ $\Rightarrow$ $\mathbf{v}_{21}^A(t)=R\Omega\left[\left(\frac{1}{\mathrm{sen}^2\beta(t)}-3\mathrm{sen}\beta(t)\right)\ \mathbf{i}_1+3\mathrm{cos}\beta(t)\ \mathbf{j}_1\right]$

2.4.2 Cálculo de la aceleración instantánea

Las propiedades del campo de aceleraciones del movimiento {21} establecen que...

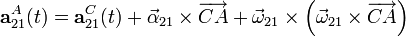
$\mathbf{a}_{21}^A(t)=\mathbf{a}_{21}^C(t)+\vec{\alpha}_{21}\times\overrightarrow{CA}+\vec{\omega}_{21}\times\left(\vec{\omega}_{21}\times\overrightarrow{CA}\right)$

donde se tendrá que...

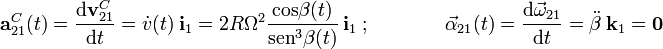
$\mathbf{a}_{21}^C(t)=\frac{\mathrm{d}\mathbf{v}_{21}^C}{\mathrm{d}t}=\dot{v}(t)\ \mathbf{i}_1=2R\Omega^2\frac{\mathrm{cos}\beta(t)}{\mathrm{sen}^3\beta(t)}\ \mathbf{i}_1\ \mathrm{;}\qquad\qquad\vec{\alpha}_{21}(t)=\frac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}=\ddot{\beta}\ \mathbf{k}_1=\mathbf{0}$

...y sustituyendo en la expresión de la acelerión instantánea del punto $A$ , se obtiene:

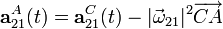
$\mathbf{a}_{21}^A(t)=\mathbf{a}_{21}^C(t)-|\vec{\omega}_{21}|^2\overrightarrow{CA}$ $\Rightarrow$ $\mathbf{a}_{21}^A(t)=R\Omega^2\left[\left(\frac{2}{\mathrm{sen}^3\beta(t)}+3\right)\cos\beta(t)\ \mathbf{i}_1+3\ \mathrm{sen}\beta(t)\ \mathbf{j}_1\right]$

Disco arrastrando una varilla

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Determinación gráfica de los C.I.R.

2.2 Reducciones cinemáticas en el punto $C$

2.2.1 Reducción del movimiento {01}

2.2.2 Reducción del movimiento {21}

2.2.3 Reducción del movimiento {20}

2.3 Vector posición del punto $A$

2.4 Velocidad y aceleración de $A$

2.4.1 Cálculo de la velocidad instantánea

2.4.2 Cálculo de la aceleración instantánea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Disco arrastrando una varilla

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Determinación gráfica de los C.I.R.

2.2 Reducciones cinemáticas en el punto C

2.2.1 Reducción del movimiento {01}

2.2.2 Reducción del movimiento {21}

2.2.3 Reducción del movimiento {20}

2.3 Vector posición del punto A

2.4 Velocidad y aceleración de A

2.4.1 Cálculo de la velocidad instantánea

2.4.2 Cálculo de la aceleración instantánea

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.2 Reducciones cinemáticas en el punto $C$

2.3 Vector posición del punto $A$

2.4 Velocidad y aceleración de $A$