Inducción electromagnética
De Laplace
(→Energía almacenada en un sistema de corrientes) |
(→Ley de inducción de Faraday) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 4: | Línea 4: | ||
En situaciones de campos variables en el tiempo deja de cumplirse que el campo eléctrico sea irrotacional. | En situaciones de campos variables en el tiempo deja de cumplirse que el campo eléctrico sea irrotacional. | ||
| - | Cuando se tiene una espira | + | Cuando se tiene una espira <math>\Gamma</math> que, en general, puede moverse o deformarse en el seno de un campo magnético variable en el tiempo, se |
induce una fuerza electromotriz a lo largo de la espira que verifica la ''ley de Faraday'' en forma integral | induce una fuerza electromotriz a lo largo de la espira que verifica la ''ley de Faraday'' en forma integral | ||
| Línea 34: | Línea 34: | ||
aunque en esta forma sólo es aplicable a superficies inmóviles. | aunque en esta forma sólo es aplicable a superficies inmóviles. | ||
| - | El signo negativo que precede a la derivada del flujo en la ley de Faraday implica la | + | El signo negativo que precede a la derivada del flujo en la ley de Faraday implica la ''ley de Lenz'': el sentido de la corriente |
inducida en la espira es tal que se opone a la variación del flujo magnético. | inducida en la espira es tal que se opone a la variación del flujo magnético. | ||
última version al 16:37 10 abr 2013
Contenido |
1 Introducción
2 Ley de inducción de Faraday
En situaciones de campos variables en el tiempo deja de cumplirse que el campo eléctrico sea irrotacional.
Cuando se tiene una espira Γ que, en general, puede moverse o deformarse en el seno de un campo magnético variable en el tiempo, se induce una fuerza electromotriz a lo largo de la espira que verifica la ley de Faraday en forma integral
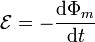
siendo Φm el flujo magnético calculado sobre cualquier superficie apoyada en la curva Γ y orientada según la regla de la mano derecha respecto al sentido de recorrido de Γ.
Esta fuerza electromotriz contiene términos eléctricos y magnéticos, de acuerdo con la ley de fuerza de Lorentz
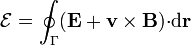
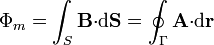
En principio, la ley de Faraday requiere una espira material en la cual las cargas experimenten la fuerza de Lorentz. Maxwell extendió este resultado a una relación entre campos. Aplicando el teorema de Stokes a la versión integral se obtiene la forma diferencial de la ley de Faraday
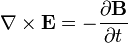
que nos dice que el campo eléctrico posee fuentes vectoriales asociadas a la variación del campo magnético (ausentes, por tanto, en electrostática). Esto implica que deja de existir el potencial eléctrico y el concepto de diferencia de potencial, siendo sustituido por el de voltaje
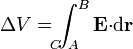
donde es necesario indicar el camino C a lo largo del cual se calcula la integral.
La condición de salto asociada a la ley de Faraday es la misma que en situaciones electrostáticas
![\mathbf{n}\times[\mathbf{E}] = \mathbf{0}](/wiki/images/math/6/d/9/6d9a6f945a9f8273282ed8720257a0ba.png)
aunque en esta forma sólo es aplicable a superficies inmóviles.
El signo negativo que precede a la derivada del flujo en la ley de Faraday implica la ley de Lenz: el sentido de la corriente inducida en la espira es tal que se opone a la variación del flujo magnético.
3 Coeficientes de inducción mutua y autoinducción
Como consecuencia de la ley de Faraday y de la ley de Biot y Savart, si tenemos una espira por la cual circula una corriente variable en el tiempo, se genera un campo magnético también variable, que induce una fuerza electromotriz sobre la propia espira. Éste es el efecto de la autoinducción.
Al ser el campo proporcional a la corriente que lo crea, también lo es el flujo magnético
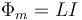
siendo L el coeficiente de autoinducción, que se mide en Henrios (siendo 1 H = 1 T·m²/A). Este coeficiente depende exclusivamente de la geometría del circuito y no de la corriente que fluye por él.
De esta forma, la f.e.m. inducida en el propio circuito es
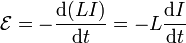
Siendo precisos, el coeficiente L sólo puede extraerse de la derivada cuando el circuito es rígido.
Si la espira se encuentra sometida además a otros campos externos variables, el efecto de la autoinducción se suma a la f.e.m. externa, de forma que
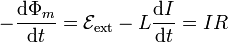
o, equivalentemente
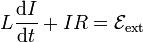
en la que el término de autoinducción se lee como una caída de tensión vL = L(dI / dt) (aunque no se trate exactamente de un voltaje).
Aunque la autoinducción es una propiedad global del circuito, se representa como un elemento localizado, puesto en serie con la resistencia del circuito. De esta forma, una sola espira metálica sometida a un campo externo se representa por tres elementos.
Un caso particular importante de coeficiente de autoinducción es el del solenoide recto de gran longitud. Al conectar sus extremos tenemos una espira cerrada en forma de hélice.
Para una bobina, aunque técnicamente consiste en una sola espira, el flujo total puede calcularse sumando los flujos a través de cada una de las vueltas de la hélice, consideradas como espiras independientes. A su vez, el campo debido al solenoide es conocido. Todo esto da el coeficiente de autoinducción
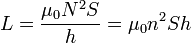
siendo N el número de espiras, S la sección transversal, h la longitud de la bobina y n = N / h la densidad de espiras.
Otro caso importante, relacionado con éste, es el de un circuito magnético simple, en el que una bobina está arrollada sobre un núcleo toroidal de alta permeabilidad μ. En este caso el coeficiente de autoinducción es, aproximadamente
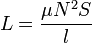
siendo l la longitud del núcleo y S su sección.
Si en lugar de una sola espira tenemos varias, por las cuales circulan sendas intensidades Ii el flujo magnético a través de cada una será una combinación lineal de las intensidades respectivas
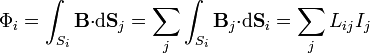
Los coeficientes Lij forman una matriz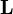 
, de la cual los elementos diagonales son los coeficientes de autoinducción (siempre positivos) y los Lij, con 
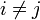, son los coeficientes de inducción mutua, que pueden ser positivos, negativos o nulos. Esta matriz es siempre simétrica.
Para un sistema de varias espiras, la fuerza electromotriz inducida en cada una dependerá de todas las corrientes
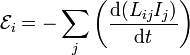
En circuitos formados por dispositivos fijos, los coeficientes pueden salir de las derivadas, pero en motores, generadores y otros dispositivos, no es extraño que los coeficientes dependan del tiempo, debido al movimiento de unas espiras respecto a otras. Por ello, hay que ser precavido con el cálculo de la derivada.
En el caso particular de sólo dos espiras suele usarse la notación abreviada
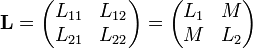
Para estos sistemas se define el coeficiente de acoplamiento entre los circuitos
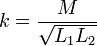
este coeficiente está siempre comprendido en el intervalo (−1,1). Si M = 0 las espiras no se influyen mutuamente. Si | k | = 1 el acoplamiento es total.
En el caso de acoplamiento total se dice que tenemos un transformador. Un ejemplo típico es el dos bobinas (llamadas respectivamente el primario y el secundario) con diferente número de espiras arrolladas sobre el mismo núcleo. Para un transformador ideal (sin pérdidas) se verifica que la tensión medida entre los bornes del primario y los del secundario son proporcionales entre sí
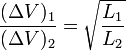
En un transformador real deben añadirse los efectos de la resistencia finita de los solenoides, así como las pérdidas óhmicas en el núcleo.
4 Generadores, motores y transformadores
5 Energía magnética
5.1 Disipación por corrientes de Foucault
Un campo magnético puede disipar energía cinética, eléctrica o de otro tipo, a través de las pérdidas por efecto Joule asociadas a las corrientes inducidas. Estas corrientes que aparecen en el interior de metales sometidos a campos variables se denominan corrientes de Foucault y son responsables de efectos que pueden ser indeseados (como el calentamiento de núcleos de transformadores), pero también deseables (como en los hornos de inducción).
Un caso de interés es el de los frenos magnéticos en el que un metal en movimiento se ve sometido a un campo magnético. Éste induce corrientes cuyas pérdidas provienen de la energía cinética, resultando en un frenado muy efectivo del metal. Desde el punto de vista mecánico, el efecto de frenado puede entenderse a través de la fuerza que el campo magnético ejerce sobre las corrientes que el mismo induce.
5.2 Energía almacenada en un sistema de corrientes
En un circuito simple, que posea una autoinducción no nula, para establecer una corriente estacionaria, un generador debe realizar un trabajo extra, para vencer la f.e.m. que se le opone, de acuerdo con la ley de Lenz. El resultado es
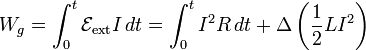
El segundo término no es energía disipada, sino almacenada en el sistema, que puede liberarse cuando se desconecta el generador (posiblemente en forma de chispa). Esta energía magnética puede considerarse asociada a las corrientes estacionarias. Más en general, si tenemos un sistema de espiras, por las cuales circulan corrientes Ii, la energía magnética es
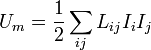
En términos de las corrientes y los flujos magnéticos queda
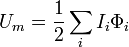
Esta expresión puede extenderse a una densidad de corriente de volumen como
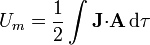
Aplicando la ley de Ampère, la energía magnética se expresa como la integral de una densidad de energía
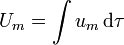
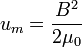
Esta expresión es válida para campos magnéticos en el vacío. Si existen medios materiales no hay expresión general. La excepción son los medios lineales, en los que basta sustituir μ0 por μ.
En sistemas de corrientes distribuidas, la identificación del resultado de hallar Um, hallado integrando la densidad de energía, con el sumatorio en función de las corrientes y coeficientes es la herramienta que permite calcular los coeficientes Lij.
