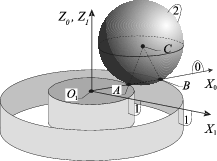Entrar Página Discusión Historial Go to the site toolbox

Problemas de Movimiento relativo (G.I.A.)

De Laplace

(Diferencias entre revisiones)
(→Disco contenido en un plano que rota)
(→Dos ventiladores)
Línea 70: Línea 70:
==[[ Dos ventiladores (G.I.A.) | Dos ventiladores  ]]==
==[[ Dos ventiladores (G.I.A.) | Dos ventiladores  ]]==
-
[[Imagen:F1_GIA_ventiladores_enunciado.png|right]]
+
[[Imagen:ventiladores.gif|right]]
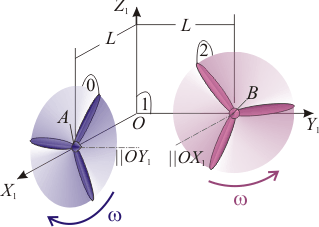
Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos "0" y "2") de orientación fija, ambos a la misma altura, y con sus respectivos centros (<math>A</math> y <math>B</math>) equidistantes (distancia <math>L</math>) de la esquina (punto <math>O</math>). Los dos ventiladores rotan con velocidad angular de módulo constante e igual a <math>\omega</math>, con las orientaciones y sentidos dados en la figura. Definido el triedro fijo <math>OXYZ</math> (sólido "1") del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determina:
Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos "0" y "2") de orientación fija, ambos a la misma altura, y con sus respectivos centros (<math>A</math> y <math>B</math>) equidistantes (distancia <math>L</math>) de la esquina (punto <math>O</math>). Los dos ventiladores rotan con velocidad angular de módulo constante e igual a <math>\omega</math>, con las orientaciones y sentidos dados en la figura. Definido el triedro fijo <math>OXYZ</math> (sólido "1") del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determina:
# Los vectores <math>\vec{\omega}_{20}</math> y <math>\vec{\alpha}_{20}</math>.  Los vectores <math>\vec{v}_{20}^O</math> y <math>\vec{a}_{20}^O</math>.  
# Los vectores <math>\vec{\omega}_{20}</math> y <math>\vec{\alpha}_{20}</math>.  Los vectores <math>\vec{v}_{20}^O</math> y <math>\vec{a}_{20}^O</math>.  

Revisión de 10:33 22 dic 2011

Contenido

1 Giro de un triedro

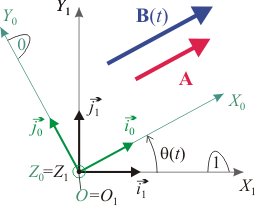
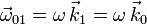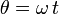Los triedros O1X1Y1Z1 y OX0Y0Z0 están definidos de modo que sus orígenes y los ejes O1Z1 coinciden. El triedro "1" está en reposo y el triedro "0" gira respecto al "1" con velocidad angular uniforme \vec{\omega}_{01} = \omega\,\vec{k}_1 =\omega\,\vec{k}_0, de modo que el ángulo θ indicado en la figura es \theta = \omega\, t.

  1. Calcula las derivadas de los vectores de la base del triedro "0" vistos desde el triedro "1".
  2. Dado el vector 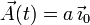\vec{A}(t) = a\,\vec{\imath}_0 calcula

\left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_1 \qquad\qquad \left.\dfrac{\mathrm{d}\vec{A}}{\mathrm{d}t}\right|_0

  1. Expresa el resultado en los vectores de la base móvil (triedro "0") y la base fija (triedro "1").
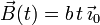
  2. Haz el mismo cálculo para el vector \vec{B}(t) = b\,t\,\vec{\imath}_0

2 Movimiento relativo de un coche y un tren

Un tren circula por una vía recta con velocidad uniforme vt. Un coche se aleja de un paso a nivel perpendicularmente al tren con velocidad vc. Encuentra la velocidad del coche vista por un observador que se mueve con el tren y por un observador en el paso a nivel. Describe las trayectorias que describe el coche para cada uno de estos observadores.

3 Coche sobre una plataforma circular

Una plataforma circular gira alrededor de un eje perpendicular a ella que pasa por su centro con velocidad angular uniforme ω. Un coche se mueve radialmente desde el centro de la plataforma hacia fuera con velocidad uniforme vc. Encuentra la expresión de la velocidad del coche visto desde la plataforma y desde un observador en reposo absoluto. Describe las trayectorias que describe el coche para cada uno de estos observadores.

Ayuda

\begin{array}{ccc} \displaystyle\int t\,\,\mathrm{sen}\,(\omega t)\mathrm{d} t = -\dfrac{t}{\omega}\cos(\omega t) + \dfrac{1}{\omega^2}\,\mathrm{sen}\,(\omega t)& \qquad &\displaystyle\int t\,\cos(\omega t)\mathrm{d} t = \dfrac{t}{\omega}\,\mathrm{sen}\,(\omega t) + \dfrac{1}{\omega^2}\cos(\omega t) \end{array}

4 Disco engarzado en otro disco

En la figura se muestra un disco de radio R (sólido "2"), que gira con velocidad angular ω20(t) = ω, constante, alrededor del eje perpendicular a él, O1X0. Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante ω01(t) = Ω, alrededor del eje vertical O1Z1 de un sistema de referencia fijo O1X1Y1Z1 (sólido "1"). Determina las magnitudes cinemáticas \vec{v}^B_{21} y \vec{a}^B_{21} en el instante representado en la figura.

 

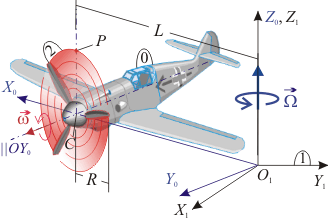
5 Hélice de un avión que gira

El avión (sólido "0") de la figura se mueve de modo que el centro C de su hélice describe una circunferencia de radio L. La velocidad angular de este giro es uniforme y su módulo es 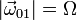|\vec{\omega}_{01}|=\Omega. Además, la hélice (sólido "2"), cuyo radio es R, gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad también uniforme y de módulo 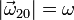|\vec{\omega}_{20}|=\omega. Se pide

  1. La reducción cinemática de los movimientos {01} y {20}.
  2. Aplicando la composición de velocidades, la velocidad 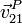\vec{v}_{21}^P y aceleración 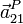\vec{a}_{21}^P del punto más alto de la hélice (punto P en la figura).
  3. La reducción cinemática del movimiento {21} en P y la ecuación del E.I.R.M.D. ¿Qué tipo de movimiento describe la hélice respecto al sólido "1"?
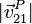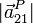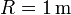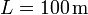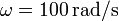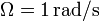  4. Calcule numéricamente |\vec{v}_{21}^P| y |\vec{a}_{21}^P| para los valores R=1\,\mathrm{m}, L=100\,\mathrm{m}, \omega=100\,\mathrm{rad/s} y \Omega=1\,\mathrm{rad/s}.

Nota: Se recomienda utilizar el triedro asociado al sólido "0" para resolver el problema.

6 Disco contenido en un plano que rota

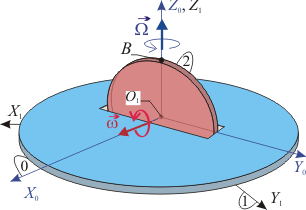
Un plano vertical Π ( sólido "0"), gira alrededor del eje vertical fijo O1Z1 con su eje O1X0 siempre contenido en el plano horizontal fijo O1X1Y1 ( sólido "1"), estando caracterizado dicho movimiento por el vector rotación 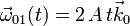\vec{\omega}_{01}(t)=2\,A\,t\vec{k}_0. Un disco de centro O y radio R (sólido "2"), contenido en todo instante en el plano Π, rueda sin deslizar sobre el eje horizontal O1X0, siendo la velocidad relativa de su centro 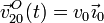\vec{v}_{20}^O(t)=v_0\vec{\imath}_0 (con v0 constante). Si en el instante inicial (t = 0), el centro O se encontraba en el eje O1Z1, determina:

  1. Los vectores velocidad angular 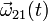\vec{\omega}_{21}(t) y aceleración angular 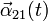\vec{\alpha}_{21}(t) en un instante cualquiera.
  2. Los vectores aceleración 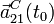\vec{a}_{21}^C(t_0) en un instante t = t0 en el que el punto C del disco se halla en contacto con el plano horizontal O1X1Y1.
  3. El eje instantáneo de rotación y mínimo deslizamiento del movimiento {21} en el citado instante t = t0.

7 Disco y vástago

El sólido rígido "0" del mecanismo de la figura corresponde a un vástago OC de longitud 3R que, mediante un par cilíndrico situado en su extremo O, permanece en todo instante perpendicular al eje vertical fijo O1Z1 (sólido "1"). Dicho par de enlace permite que el vástago gire alrededor de O1Z1 con velocidad angular constante de módulo 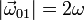|\vec{\omega}_{01}|=2\omega y en el sentido mostrado en la figura; a su vez, el extremo O se desplaza sobre el eje vertical O1Z1 en sentido positivo y con velocidad constante, siendo el módulo de ésta 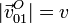|\vec{v}_{01}^O|=v. El extremo C del sólido "0" está articulado al centro de un disco de radio R (sólido "2"), siempre contenido en el plano vertical OX0Z0; el movimiento relativo del disco respecto del vástago consiste en una rotación permanente alrededor de un eje paralelo a OY0 que pasa por C, en el sentido indicado en la figura y con velocidad angular constante de módulo 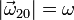|\vec{\omega}_{20}|=\omega. Utilizando la base vectorial del triedro ligado al sólido "0"- OX0Y0Z0 - para expresar las magnitudes vectoriales, determina:

  1. El vector rotación instantánea \vec{\omega}_{21} y su derivada temporal 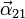\vec{\alpha}_{21} (vector aceleración angular), correspondientes al movimiento del disco respecto al triedro fijo.
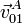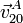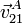  2. Las velocidades del punto A del perímetro del disco en el instante en el que aquél ocupa el punto más alto del diámetro vertical(ver figura), para cada uno de los tres movimientos relativos que se distinguen en el mecanismo descrito: \vec{v}_{01}^A, \vec{v}_{20}^A y \vec{v}_{21}^A.
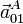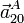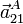  3. Las aceleraciones \vec{a}_{01}^A, \vec{a}_{20}^A y \vec{a}_{21}^A para el mismo punto y en el mismo instante especificado en el apartado anterior.

8 Esfera sobre dos raíles

Una esfera de radio R (sólido "2"), se desplaza sobre dos carriles circulares concéntricos fijos de radios R y 2R (sólido "1"), situados en un plano horizontal (ver figura). El movimiento de la esfera es tal que: i) en todo instante, rueda sin deslizar sobre ambos carriles, y ii) su centro C realiza un movimiento circular uniforme, siendo v0 el módulo de su velocidad. Considerando cómo sólido móvil intermedio (sólido "0") al plano O1X0Z0 que contiene en todo instante al centro C de la esfera (ver figura), calcula:

  1. Los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
  2. Reducciones cinemáticas de dichos movimientos,
  3. Para el punto de la esfera en contacto con el carril de mayor diámetro (punto B), los vectores 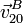\vec{v}_{20}^B y \vec{a}_{21}^B

9 Dos ventiladores

Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos "0" y "2") de orientación fija, ambos a la misma altura, y con sus respectivos centros (A y B) equidistantes (distancia L) de la esquina (punto O). Los dos ventiladores rotan con velocidad angular de módulo constante e igual a ω, con las orientaciones y sentidos dados en la figura. Definido el triedro fijo OXYZ (sólido "1") del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determina:

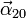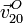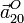  1. Los vectores \vec{\omega}_{20} y \vec{\alpha}_{20}. Los vectores \vec{v}_{20}^O y \vec{a}_{20}^O.
  2. El eje instantáneo de rotación.

Nota: Se recomienda usar el triedro "1" y su base vectorial para resolver el ejercicio.

10 Partícula girando en un aro

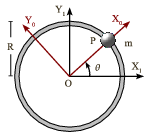
Una partícula describe un movimiento circular de radio R con velocidad angular uniforme ω. Se considera que no hay rozamiento ni peso.

  1. Aplicando la Segunda Ley de Newton en el sistema en reposo, calcula la fuerza neta ejercida sobre la partícula en cada instante.
  2. Se considera una escuadra OX0Y0, de modo que el eje OX0 pasa siempre por el centro de la circunferencia y la posición de la partícula en cada instante. Aplica la Segunda Ley de Newton en este sistema de referencia no inercial.

11 Partícula en un tubo que gira

Analiza el problema 8 del boletín de Dinámica del punto utilizando el sistema de referencia no inercial solidario con el tubo que gira.

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_Movimiento_relativo_(G.I.A.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace