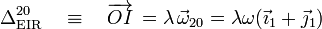Dos ventiladores (G.I.A.)

De Laplace

1 Enunciado

Sobre dos paredes perpendiculares, se han colocado sendos ventiladores planos (sólidos "0" y "2") de orientación fija, ambos a la misma altura, y con sus respectivos centros (A y B) equidistantes (distancia L) de la esquina (punto O). Los dos ventiladores rotan con velocidad angular de módulo constante e igual a ω, con las orientaciones y sentidos dados en la figura. Definido el triedro fijo OXYZ (sólido "1") del esquema, y considerando, como movimiento-problema, el movimiento relativo entre ambos ventiladores (movimiento {20}), determina:

1. Los vectores y 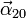. Los vectores 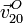y .
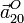2. El eje instantáneo de rotación.

"'Nota:"' Se recomienda usar el triedro "1" y su base vectorial para resolver el ejercicio.

2 Solución

2.1 Vectores y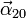

En este problema se usa el sólido "1", en reposo absoluto, como sólido intermedio. Es decir, usaremos la composición

Los datos cinemáticos proporcionados por el enunciado son, expresados en la base del sólido "1",

Podemos calcular las aceleraciones angulares derivando en el tiempo, pues los ejes de giro de cada ventilador son permanentes

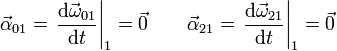
La velocidad y aceleración angulares pedidas son

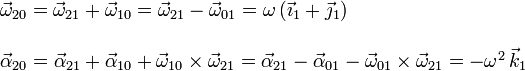
2.2 Vectores 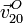y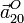

Vamos a determinar la velocidad y aceleración en cada uno de los movimientos de la composición.

2.2.1 Movimiento {01}

El punto A es un punto fijo de la rotación {01}, pues está en el eje permanente de rotación. Entonces

A partir de aquí podemos calcular 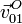y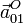

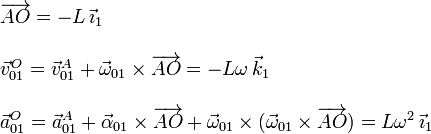
2.2.2 Movimiento {21}

El punto B es un punto fijo de la rotación {21}, pues está en el eje permanente de rotación. Entonces

A partir de aquí podemos calcular 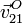y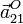

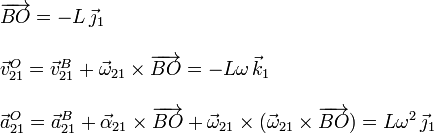
Ahora podemos calcular los vectores pedidos. Veamos 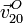en primer lugar

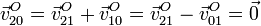
Para la aceleración tenemos

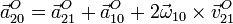
Aquí hay que tener cuidado, pues en general 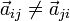, como hemos usado en los casos anteriores. Por ello, vamos a usar la descomposición {21}={20}+{01}

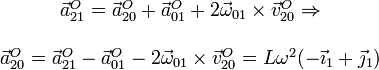
2.3 Eje instantáneo de rotación

Como 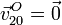, el punto O esta en el eje. Entonces su ecuación paramétrica es