Disco engarzado en otro disco (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

En la figura se muestra un disco de radio $R$ (sólido "2"), que gira con velocidad angular $ω 20 (t) = ω$ , constante, alrededor del eje perpendicular a él, $O 1 X 0$ . Dicho eje está rígidamente unido a una plataforma (sólido "0"), que gira también con velocidad angular constante $ω 01 (t) = Ω$ , alrededor del eje vertical $O 1 Z 1$ de un sistema de referencia fijo $O 1 X 1 Y 1 Z 1$ (sólido "1"). Determina las magnitudes cinemáticas $\vec{v}^B_{21}$ y $\vec{a}^B_{21}$ en el instante representado en la figura.

2 Solución

El problema nos pide determinar el movimiento del punto $B$ , perteneciente al sólido "2", en el instante en que se encuentra en su punto más alto. El movimiento {21} puede descomponerse en la rotación del sólido "0" respecto al eje $O 1 Z 1$ y la rotación del sólido "2" respecto al eje $O 1 X 0$ :

{21} = {20} + {01}

Analicemos en detalle estos dos movimientos

2.1 Movimiento {01}

La reducción de un movimiento consiste en calcular su velocidad angular y la velocidad de uno de los puntos del sólido. Con eso podemos determinar el eje instantáneo de rotación. Para poder determinar la aceleración de cualquier punto necesitamos también la aceleración angular y la aceleración en un punto. Esto es lo que vamos a determinar en este movimiento.

En este caso, el movimiento {01} es un rotación permanente alrededor del eje $O 1 Z 1$ . El enunciado nos dice que la velocidad angular vale 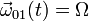$\vec{\omega}_{01}(t)=\Omega$ y es constante en el tiempo. Tenemos entonces

$\vec{\omega}_{01} = \Omega\,\vec{k}_1=\Omega\,\vec{k}_0\qquad\qquad \vec{\alpha}_{01} = \left.\dfrac{\mathrm{d}\vec{\omega}_{01}}{\mathrm{d}t}\right|_1=\vec{0}$

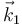Hemos usado el hecho de que, en este problema, los ejes $O 1 Z 0$ y $O 1 Z 1$ son iguales entre sí e invariantes en el tiempo. Esto nos permite, por un lado, expresar $\vec{\omega}_{01}$ en función de $\vec{k}_0$ ó $\vec{k}_1$ , y por otro lado hacer la derivada temporal suponiendo que 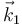$\vec{k}_1$ no cambia en el tiempo, con lo cual 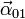$\vec{\alpha}_{01}$ es nula. Dado que el eje de rotación es invariante en el tiempo, los puntos en él tienen velocidad y aceleración nula. Escogiendo, por ejemplo, el origen $O 1$ , podemos caracterizar completamente el movimiento {01}

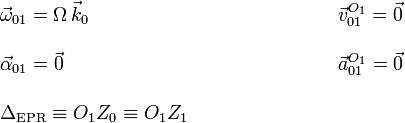
$\begin{array}{lcl} \vec{\omega}_{01}=\Omega\,\vec{k}_0&\qquad\qquad\qquad&\vec{v}_{01}^{O_1}=\vec{0}\\ &&\\ \vec{\alpha}_{01}=\vec{0}&\qquad\qquad\qquad&\vec{a}_{01}^{O_1}=\vec{0} \\ &&\\ \Delta_{\mathrm{EPR}}\equiv O_1Z_0\equiv O_1Z_1 \end{array}$

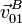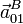Como queremos determinar el movimiento del punto $B$ , vamos a calcular $\vec{v}_{01}^{B}$ y $\vec{a}_{01}^{B}$ . Utilizamos las ecuaciones del campo de velocidades y aceleraciones del sólido "0"

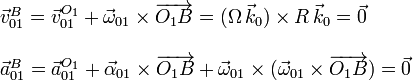
$\begin{array}{l} \vec{v}_{01}^{B} = \vec{v}_{01}^{O_1}+\vec{\omega}_{01}\times\overrightarrow{O_1B}= (\Omega\,\vec{k}_0)\times{R\,\vec{k}_0}=\vec{0}\\ \\ \vec{a}_{01}^{B} = \vec{a}_{01}^{O_1}+\vec{\alpha}_{01}\times\overrightarrow{O_1B} + \vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{O_1B})=\vec{0} \end{array}$

Este resultado es razonable, pues el punto $B$ pertenece al eje de giro del movimiento.

2.2 Movimiento {20}

En este caso tenemos una rotación alrededor de un eje perpendicular al sólido "2". Hemos elegido el eje $O 1 X 0$ coincidiendo con este eje de giro. El enunciado dice que la velocidad angular $ω 20$ es constante en el tiempo, por tanto

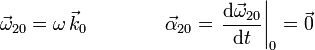
$\vec{\omega}_{20} = \omega\,\vec{k}_0\qquad\qquad \vec{\alpha}_{20} = \left.\dfrac{\mathrm{d}\vec{\omega}_{20}}{\mathrm{d}t}\right|_0=\vec{0}$

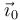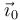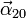En este caso, como el sólido derivador es el "0", y la expresión de $\vec{\omega}_{20}$ en función de $\vec{\imath}_0$ es válida en cualquier instante de tiempo, podemos hacer la derivada suponiendo $\vec{\imath}_0$ constante, con lo que $\vec{\alpha}_{20}$ resulta ser nula.

Como el eje de rotación es la recta $O 1 X 0$ , el punto $O 1$ es de nuevo un punto fijo de este movimiento. Por tanto, la caracterización del movimiento {20} es

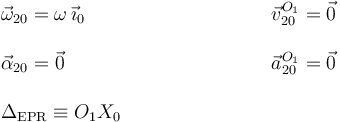
$\begin{array}{lcl} \vec{\omega}_{20}=\omega\,\vec{\imath}_0&\qquad\qquad\qquad&\vec{v}_{20}^{O_1}=\vec{0}\\ &&\\ \vec{\alpha}_{20}=\vec{0}&\qquad\qquad\qquad&\vec{a}_{20}^{O_1}=\vec{0} \\ &&\\ \Delta_{\mathrm{EPR}}\equiv O_1X_0 \end{array}$

Determinamos también los vectores 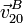$\vec{v}_{20}^{B}$ y $\vec{a}_{20}^{B}$

$\begin{array}{l} \vec{v}_{20}^{B} = \vec{v}_{20}^{O_1}+\vec{\omega}_{20}\times\overrightarrow{O_1B}= (\omega\,\vec{\imath}_0)\times{R\,\vec{k}_0}=-R\,\omega\,\vec{\jmath}_0\\ \\ \vec{a}_{20}^{B} = \vec{a}_{20}^{O_1}+\vec{\alpha}_{20}\times\overrightarrow{O_1B} + \vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{O_1B})=-R\,\omega^2\,\vec{k}_0 \end{array}$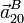

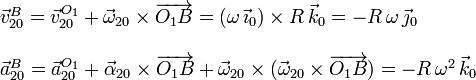
En este movimiento, el punto $B$ realiza un movimiento circular uniforme, con lo cual es razonable que 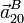$\vec{a}_{20}^{B}$ apunte hacia el punto $O 1$ .

2.3 Movimiento {21}

Podemos describir este movimiento como combinación de los otros dos {21}={20}+{01}. Tenemos

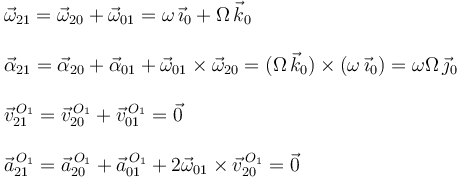
$\begin{array}{l} \vec{\omega}_{21} = \vec{\omega}_{20}+\vec{\omega}_{01} = \omega\,\vec{\imath}_0+\Omega\,\vec{k}_0\\ \\ \vec{\alpha}_{21} = \vec{\alpha}_{20}+\vec{\alpha}_{01} +\vec{\omega}_{01}\times\vec{\omega}_{20} = (\Omega\,\vec{k}_0)\times(\omega\,\vec{\imath}_0) = \omega\Omega\,\vec{\jmath}_0\\ \\ \vec{v}_{21}^{\,O_1} = \vec{v}_{20}^{\,O_1}+\vec{v}_{01}^{\,O_1}=\vec{0}\\ \\ \vec{a}_{21}^{\,O_1} = \vec{a}_{20}^{\,O_1}+\vec{a}_{01}^{\,O_1} + 2\vec{\omega}_{01}\times\vec{v}^{\,O_1}_{20}=\vec{0} \end{array}$

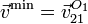El eje instantáneo de rotación es paralelo a $\vec{\omega}_{21}$ y pasa por $O 1$ , pues $\vec{v}^{\mathrm{min}}=\vec{v}_{21}^{O_1}$ , pues ésta es cero. Así pues, la caracterización del movimiento {21} es

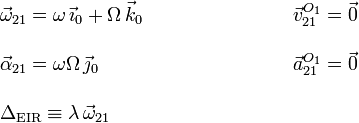
$\begin{array}{lcl} \vec{\omega}_{21}=\omega\,\vec{\imath}_0+\Omega\,\vec{k}_0&\qquad\qquad\qquad&\vec{v}_{21}^{O_1}=\vec{0}\\ &&\\ \vec{\alpha}_{21}=\omega\Omega\,\vec{\jmath}_0&\qquad\qquad\qquad&\vec{a}_{21}^{O_1}=\vec{0} \\ &&\\ \Delta_{\mathrm{EIR}}\equiv \lambda\, \vec{\omega}_{21} \end{array}$

Es interesante observar que la combinación de dos rotaciones con velocidad angular constante da una rotación con aceleración angular no nula. Esto se debe a que la dirección de $Δ EIR$ cambia con el tiempo. El vector 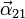$\vec{\alpha}_{21}$ apunta en la dirección en que se produce este cambio.

2.4 Velocidad y aceleración del punto B

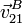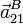Ahora podemos calcular $\vec{v}_{21}^{B}$ y $\vec{a}_{21}^{B}$ . Si usamos la composición {21}={20}+{01} podemos utilizar las velocidades y aceleraciones calculadas anteriormente

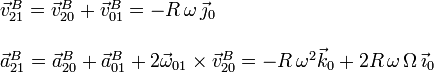
$\begin{array}{l} \vec{v}_{21}^{B} = \vec{v}_{20}^B+\vec{v}_{01}^B = -R\,\omega\,\vec{\jmath}_0\\ \\ \vec{a}_{21}^{B} = \vec{a}_{20}^B+\vec{a}_{01}^B +2\vec{\omega}_{01}\times\vec{v}_{20}^B=-R\,\omega^2\vec{k}_0+2R\,\omega\,\Omega\,\vec{\imath}_0 \end{array}$

También podemos hacer el cálculo a partir de la reducción del movimiento {21} y usando el campo de velocidades y aceleraciones de este movimiento

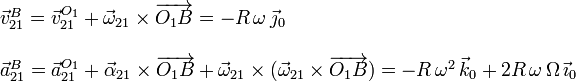
$\begin{array}{l} \vec{v}_{21}^{B} = \vec{v}_{21}^{O_1}+\vec{\omega}_{21}\times\overrightarrow{O_1B}= -R\,\omega\,\vec{\jmath}_0\\ \\ \vec{a}_{21}^{B} = \vec{a}_{21}^{O_1}+\vec{\alpha}_{21}\times\overrightarrow{O_1B} + \vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{O_1B})=-R\,\omega^2\,\vec{k}_0+2R\,\omega\,\Omega\,\vec{\imath}_0 \end{array}$

En la figura se muestran las magnitudes cinemáticas mas relevantes del problema.

Disco engarzado en otro disco (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {01}

2.2 Movimiento {20}

2.3 Movimiento {21}

2.4 Velocidad y aceleración del punto B

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES