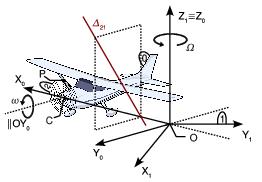
Hélice de un avión que gira (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

El avión (sólido "0") de la figura se mueve de modo que el centro $C$ de su hélice describe una circunferencia de radio $L$ . La velocidad angular de este giro es uniforme y su módulo es 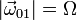$|\vec{\omega}_{01}|=\Omega$ . Además, la hélice (sólido "2"), cuyo radio es $R$ , gira en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad también uniforme y de módulo 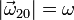$|\vec{\omega}_{20}|=\omega$ . Se pide

La reducción cinemática de los movimientos {01} y {20}.
Aplicando la composición de velocidades, la velocidad 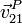$\vec{v}_{21}^P$ y aceleración 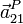$\vec{a}_{21}^P$ del punto más alto de la hélice (punto $P$ en la figura).
La reducción cinemática del movimiento {21} en $P$ y la ecuación del E.I.R.M.D. ¿Qué tipo de movimiento describe la hélice respecto al sólido "1"?
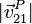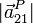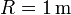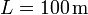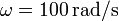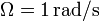Calcule numéricamente $|\vec{v}_{21}^P|$ y $|\vec{a}_{21}^P|$ para los valores $R=1\,\mathrm{m}$ , $L=100\,\mathrm{m}$ , $\omega=100\,\mathrm{rad/s}$ y $\Omega=1\,\mathrm{rad/s}$ .

Nota: Se recomienda utilizar el triedro asociado al sólido "0" para resolver el problema.

2 Solución

2.1 Reducción cinemática de {01}

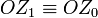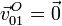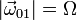El movimiento {01} es un rotación permanente cuyo eje es la recta $OZ_1\equiv OZ_0$ . El punto $O$ pertenece al eje de giro, por lo que $\vec{v}_{01}^{O}=\vec{0}$ . El enunciado dice que el módulo de la velocidad angular es $|\vec{\omega}_{01}|=\Omega$ . Según el giro que se indica en la figura apunta en el sentido positivo del eje $Z 0$ . Por tanto la reducción en el punto $O$ es

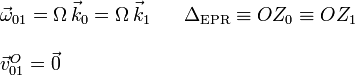
$\begin{array}{lcl} \vec{\omega}_{01}=\Omega\,\vec{k}_0=\Omega\,\vec{k}_1&&\Delta_{\mathrm{EPR}}\equiv OZ_0\equiv OZ_1\\ &&\\\vec{v}_{01}^{O}=\vec{0}&& \end{array}$

2.2 Reducción cinemática de {20}

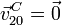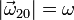Este movimiento es un rotación instantánea alrededor de la línea que pasa por el centro de la hélice y es perpendicular a ella. Así pues, el punto $C$ pertenece al eje de giro, por lo que $\vec{v}_{20}^{C}=\vec{0}$ . En el dibujo también se observa que el eje de giro es paralelo a $O Y 0$ . Como el enunciado dice que el módulo de la velocidad angular es $|\vec{\omega}_{20}|=\omega$ , la reducción en el punto $C$ es

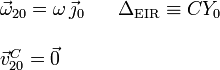
$\begin{array}{lcl} \vec{\omega}_{20}=\omega\,\vec{\jmath}_0&&\Delta_{\mathrm{EIR}}\equiv CY_0\\ && \\ \vec{v}_{20}^{C}=\vec{0} && \end{array}$

2.3 Movimiento {21}

Para encontrar las magnitudes que nos pide el problema vamos a usar la composición

{21} = {20} + {01}

La composición de velocidades angulares es

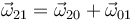
$\vec{\omega}_{21} = \vec{\omega}_{20}+\vec{\omega}_{01}$

Usando los calculos realizados tenemos

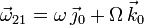
$\vec{\omega}_{21} = \omega\,\vec{\jmath}_0+\Omega\,\vec{k}_0$

Para la aceleración angular usamos

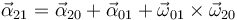
$\vec{\alpha}_{21} = \vec{\alpha}_{20}+\vec{\alpha}_{01}+\vec{\omega}_{01}\times\vec{\omega}_{20}$

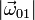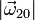El enunciado nos dice que tanto $|\vec{\omega}_{01}|$ como $|\vec{\omega}_{20}|$ son constantes. Por tanto se cumple

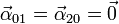
$\vec{\alpha}_{01}=\vec{\alpha}_{20}=\vec{0}$

Calculando el producto vectorial resulta

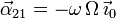
$\vec{\alpha}_{21}=-\omega\,\Omega\,\vec{\imath}_0$

Calculamos ahora 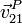$\vec{v}_{21}^P$ . Para ello usamos la composición de movimientos y, dentro de cada movimiento, la ecuación del campo de velocidades

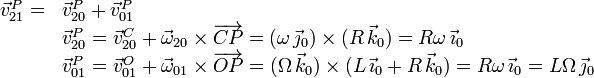
$\begin{array}{ll} \vec{v}_{21}^P=&\vec{v}_{20}^P+\vec{v}_{01}^P\\ &\vec{v}_{20}^P=\vec{v}_{20}^C+\vec{\omega}_{20}\times\overrightarrow{CP}=(\omega\,\vec{\jmath}_0)\times(R\,\vec{k}_0)=R\omega\,\vec{\imath}_0 \\ &\vec{v}_{01}^P=\vec{v}_{01}^{O}+\vec{\omega}_{01}\times\overrightarrow{OP}= (\Omega\,\vec{k}_0)\times(L\,\vec{\imath}_0+R\,\vec{k}_0)=R\omega\,\vec{\imath}_0 =L\Omega\,\vec{\jmath}_0 \end{array}$

Por tanto

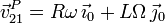
$\vec{v}_{21}^P = R\omega\,\vec{\imath}_0 + L\Omega\,\vec{\jmath}_0$

Para calcular 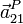$\vec{a}_{21}^P$ necesitamos determinar la aceleración en un punto de los movimientos {01} y {20}. En ambos casos, los puntos de los ejes de rotación respectivos tienen aceleración nula.Entonces

$\begin{array}{ccc} \vec{a}_{01}^{O}=\vec{0}&&\vec{a}_{20}^{C}=\vec{0} \end{array}$

Ahora podemos calcular 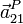$\vec{a}_{21}^P$ usando la composición y las ecuaciones del campo de velocidades de los correspondientes sólidos

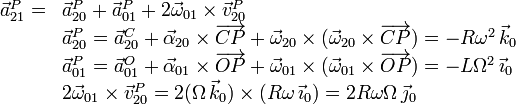
$\begin{array}{ll} \vec{a}_{21}^P =& \vec{a}_{20}^P+\vec{a}_{01}^P+2\vec{\omega}_{01}\times\vec{v}_{20}^P\\ &\vec{a}_{20}^P = \vec{a}_{20}^C +\vec{\alpha}_{20}\times\overrightarrow{CP}+\vec{\omega}_{20}\times(\vec{\omega}_{20}\times\overrightarrow{CP})= -R \omega^2\,\vec{k}_0\\ &\vec{a}_{01}^P = \vec{a}_{01}^{O} +\vec{\alpha}_{01}\times\overrightarrow{OP}+\vec{\omega}_{01}\times(\vec{\omega}_{01}\times\overrightarrow{OP})= -L \Omega^2\,\vec{\imath}_0\\ &2\vec{\omega}_{01}\times\vec{v}_{20}^P = 2(\Omega\,\vec{k}_0)\times(R\omega\,\vec{\imath}_0)= 2R\omega\Omega\,\vec{\jmath}_0 \end{array}$

Resulta

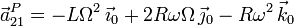
$\vec{a}_{21}^P=-L\Omega^2\,\vec{\imath}_0+2R\omega\Omega\,\vec{\jmath}_0-R\omega^2\,\vec{k}_0$

Para encontrar el eje $Δ 21$ , vamos a calcular 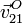$\vec{v}_{21}^O$ , para hacer más sencilla la descripción de la posición del eje. Utilizando la ecuación del campo de velocidades de {21} tenemos

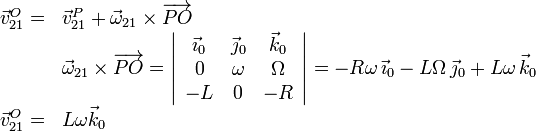
$\begin{array}{ll} \vec{v}_{21}^O =& \vec{v}_{21}^P+\vec{\omega}_{21}\times\overrightarrow{PO} \\ & \vec{\omega}_{21}\times\overrightarrow{PO} = \left| \begin{array}{ccc} \vec{\imath}_0&\vec{\jmath}_0&\vec{k}_0\\ 0&\omega&\Omega\\ -L&0&-R \end{array} \right|= -R\omega\,\vec{\imath}_0-L\Omega\,\vec{\jmath}_0+L\omega\,\vec{k}_0\\ \vec{v}_{21}^O =& L\omega\vec{k}_0 \end{array}$

Podemos encontrar un punto de $Δ 21$ usando la expresión

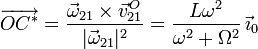
$\overrightarrow{OC^*}=\dfrac{\vec{\omega}_{21}\times\vec{v}_{21}^O}{|\vec{\omega}_{21}|^2}= \dfrac{L\omega^2}{\omega^2+\Omega^2}\,\vec{\imath}_0$

La ecuación vectorial de $Δ 21$ es

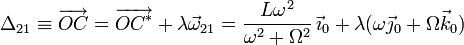
$\Delta_{21}\equiv \overrightarrow{OC} = \overrightarrow{OC^*}+\lambda\vec{\omega}_{21}= \dfrac{L\omega^2}{\omega^2+\Omega^2}\,\vec{\imath}_0 +\lambda(\omega\vec{\jmath}_0+\Omega\vec{k}_0)$

Como $ω 2 / (ω 2 + Ω 2) < 1$ , el punto $C *$ está sobre el eje $O X 0$ en un punto intermedio entre el punto $O$ y el punto $C$ . La figura muestra la posición aproximada del eje.

Para determinar el tipo de movimiento calculamos la velocidad mínima

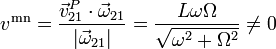
$v^{\text{mín}}=\dfrac{\vec{v}_{21}^P\cdot\vec{\omega}_{21}}{|\vec{\omega}_{21}|} = \dfrac{L\omega\Omega}{\sqrt{\omega^2+\Omega^2}} \neq 0$

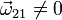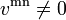Como $\vec{\omega}_{21}\neq0$ y $v^{\text{mín}}\neq0$ el movimiento instantáneo es helicoidal tangente.

2.4 Aplicación numérica

Con los valores numéricos dados y usando las expresiones de la velocidad y aceleración pedidas obtenemos

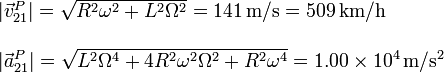
$\begin{array}{l} |\vec{v}_{21}^P| = \sqrt{R^2\omega^2+L^2\Omega^2} = 141 \,\mathrm{m/s}=509 \,\mathrm{km/h}\\ \\ |\vec{a}_{21}^P| = \sqrt{L^2\Omega^4+4R^2\omega^2\Omega^2+R^2\omega^4} = 1.00\times10^4\,\mathrm{m/s^2} \end{array}$

Damos los valores numéricos con 3 cifras significativas.

Hélice de un avión que gira (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Reducción cinemática de {01}

2.2 Reducción cinemática de {20}

2.3 Movimiento {21}

2.4 Aplicación numérica

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES