Movimiento relativo de un coche y un tren (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un tren circula por una vía recta con velocidad uniforme $v t$ . Un coche se aleja de un paso a nivel perpendicularmente al tren con velocidad $v c$ . Encuentra la velocidad del coche vista por un observador que se mueve con el tren y por un observador en el paso a nivel. Describe las trayectorias que describe el coche para cada uno de estos observadores.

2 Solución

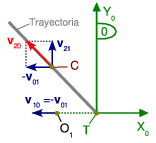
En primer lugar vamos a identificar y etiquetar los sólidos del problema. Tenemos por un lado el paso a nivel, en reposo, al que llamamos sólido "1" (identificable con el suelo). Por otro lado está el tren, al que llamamos sólido "0". Por último, el coche es el sólido "2". Cada uno de estos sólidos tiene asociado un triedro como se indica en la figura. El punto $O 1$ es el paso a nivel, el punto $C$ el coche y el punto $T$ el tren.

Los datos que nos da el problema son las velocidades del coche y del tren respecto al paso a nivel. Utilizando la notación del movimiento relativo y los ejes indicados en la figura tenemos

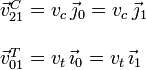
$\left. \begin{array}{l} \vec{v}^C_{21} = v_c\,\vec{\jmath}_0 = v_c\,\vec{\jmath}_1 \\ \\ \vec{v}^T_{01} = v_t\,\vec{\imath}_0 = v_t\,\vec{\imath}_1 \end{array} \right.$

El protocolo que hay que seguir para resolver este tipo de problemas consiste en encontrar la reducción en un punto de cada uno de los movimientos elementales y luego componerlos. Vamos a aplicarlo a este problema.

2.1 Movimiento {01}

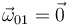Este es el movimiento del tren respecto del suelo. Es una traslación pura, por lo que $\vec{\omega}_{01}=\vec{0}$ . La velocidad es la misma en todos los puntos del sólido "0". La reducción es

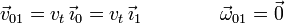
$\vec{v}_{01} = v_t\,\vec{\imath}_0 = v_t\,\vec{\imath}_1\qquad\qquad \vec{\omega}_{01}=\vec{0}$

2.2 Movimiento {21}

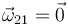Este es el movimiento del coche respecto al suelo. También es una traslación, por lo que $\vec{\omega}_{21}=\vec{0}$ . De nuevo la velocidad es la misma en todos los puntos del sólido "2". La reducción en cualquier punto es

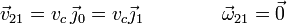
$\vec{v}_{21} = v_c\,\vec{\jmath}_0 = v_c\vec{\jmath}_1 \qquad\qquad \vec{\omega}_{21}=\vec{0}$

Esta es la velocidad con la que un observador situado en el paso a nivel ve alejarse al coche.

2.3 Movimiento {20}

Este es el movimiento del coche respecto al tren. Es el que nos piden que describamos en el enunciado. Vamos a hacerlo usando la descomposición

{21} = {20} + {01}

La ley de composición de velocidades angulares es

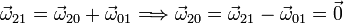
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{20} = \vec{\omega}_{21} - \vec{\omega}_{01} = \vec{0}$

Es decir, el movimiento {20} es también una traslación. En general, la composición de dos traslaciones es siempre una traslación.

Tenemos entonces que la reducción del movimiento {20} es la misma en todos los puntos. Aplicando la ley de composición de velocidades resulta

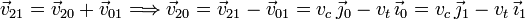
$\vec{v}_{21} = \vec{v}_{20} + \vec{v}_{01} \Longrightarrow \vec{v}_{20} = \vec{v}_{21} - \vec{v}_{01} = v_c\,\vec{\jmath}_0 - v_t\,\vec{\imath}_0 = v_c\,\vec{\jmath}_1 - v_t\,\vec{\imath}_1$

Esta es la velocidad con la que un observador montado en el tren ve alejarse el coche.

2.4 Trayectorias del coche para cada observador

Para encontrar la ecuación de la trayectoria vista por un observador en el paso a nivel (sólido "1" ) y en el tren (sólido "0") hay que encontrar el vector de posición del coche en cada uno de esos sistemas.

2.5 Trayectoria desde el paso a nivel

El vector de posición se obtiene integrando la velocidad vista desde el sistema "1". Tenemos

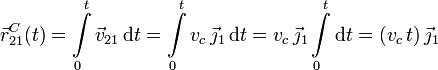
$\vec{r}^C_{21}(t) = \int\limits_0^t \vec{v}_{21}\,\mathrm{d} t = \int\limits_0^t v_c\,\vec{\jmath}_1\,\mathrm{d} t= v_c\,\vec{\jmath}_1\int\limits_0^t\mathrm{d} t= (v_c\,t)\,\vec{\jmath}_1$

Hemos expresado la velocidad en la base del sólido "1", el sólido observador en este caso. Como los vectores de la base del triedro "1" no cambian en el tiempo, pueden salir de la integral. También hemos supuesto que en $t = 0$ el coche estaba en el punto $O 1$ (en el paso a nivel). La ecuación paramétrica de la trayectoria es

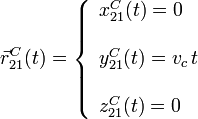
$\vec{r}^C_{21}(t) = \left\{ \begin{array}{l} x^C_{21}(t) = 0 \\ \\ y^C_{21}(t) = v_c\,t \\ \\ z^C_{21}(t) = 0 \end{array} \right.$

Esta es la ecuación de una recta que coincide con el eje $O 1 Y 1$ , como se indica en la figura.

2.6 Trayectoria desde el ten

El vector de posición se obtiene integrando la velocidad vista desde el sistema "0". Tenemos

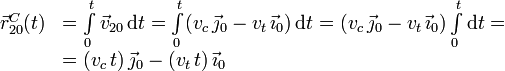
$\begin{array}{ll} \vec{r}^C_{20}(t)& = \int\limits_0^t \vec{v}_{20}\,\mathrm{d} t = \int\limits_0^t (v_c\,\vec{\jmath}_0-v_t\,\vec{\imath}_0)\,\mathrm{d} t= (v_c\,\vec{\jmath}_0 - v_t\,\vec{\imath}_0)\int\limits_0^t\mathrm{d} t=\\ &=(v_c\,t)\,\vec{\jmath}_0 - (v_t\,t)\,\vec{\imath}_0 \end{array}$

Ahora hemos expresado la velocidad en la base del sólido "0", el sólido observador en este caso. El triedro "0" no rota respecto al suelo, por lo que los vectores de la base asociados a él no cambian en el tiempo y pueden salir de la integral. También hemos supuesto que en $t = 0$ el coche estaba en el punto $O 1$ (en el paso a nivel). La ecuación paramétrica de la trayectoria es

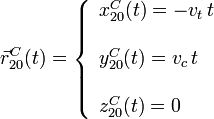
$\vec{r}^C_{20}(t) = \left\{ \begin{array}{l} x^C_{20}(t) = -v_t\,t \\ \\ y^C_{20}(t) = v_c\,t \\ \\ z^C_{20}(t) = 0 \end{array} \right.$

Esta es la ecuación de la recta mostrada en la figura.

Movimiento relativo de un coche y un tren (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {01}

2.2 Movimiento {21}

2.3 Movimiento {20}

2.4 Trayectorias del coche para cada observador

2.5 Trayectoria desde el paso a nivel

2.6 Trayectoria desde el ten

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES