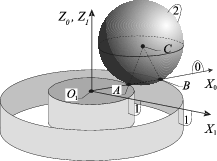Esfera sobre dos raíles (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una esfera de radio $R$ (sólido "2"), se desplaza sobre dos carriles circulares concéntricos fijos de radios $R$ y $2 R$ (sólido "1"), situados en un plano horizontal (ver figura). El movimiento de la esfera es tal que: i) en todo instante, rueda sin deslizar sobre ambos carriles, y ii) su centro $C$ realiza un movimiento circular uniforme, siendo $v 0$ el módulo de su velocidad. Considerando cómo sólido móvil intermedio (sólido "0") al plano $O 1 X 0 Z 0$ que contiene en todo instante al centro $C$ de la esfera (ver figura), calcula:

Los ejes instantáneos o permanentes de rotación de los movimientos {21}, {20} y {01}.
Reducciones cinemáticas de dichos movimientos,
Para el punto de la esfera en contacto con el carril de mayor diámetro (punto $B$ ), los vectores 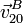$\vec{v}_{20}^B$ y $\vec{a}_{21}^B$

2 Solución

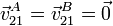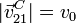Este problema es algo diferente de los anteriores. Los datos cinemáticos que nos dan son las velocidades absolutas de los puntos $A$ , $B</math> y $C</math>. Por un lado la esfera (sólido "2") rueda sin deslizar sobre los carriles (sólido "1"), por tanto $\vec{v}_{21}^A=\vec{v}_{21}^B=\vec{0}$ . Por otro lado, el centro de la esfera realiza un movimiento circular uniforme, por lo que $|\vec{v}_{21}^C|=v_0$ . Usando la base vectorial del sólido "0" que gira con el centro de la esfera, los datos cinemáticos son por tanto

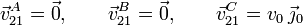
$\vec{v}_{21}^A=\vec{0},\qquad \vec{v}_{21}^B=\vec{0},\qquad \vec{v}_{21}^C=v_0\,\vec{\jmath}_0$

Además, podemos observar que el sólido "0", que sigue a la esfera en su movimiento, realiza una rotación permanente alrededor del eje $O 1 Z 1$ , de modo que podemos escribir

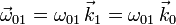
$\vec{\omega}_{01}=\omega_{01}\,\vec{k}_1=\omega_{01}\,\vec{k}_0$

Dado que tenemos la velocidad del movimiento {21} en tres puntos no alineados, esto nos permite calcular $\vec{\omega}_{21}$ . En este caso analizaremos primero el movimiento {21} y a partir de él obtendremos la descripción de los otros movimientos.

2.1 Movimiento {21}

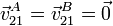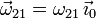Como $\vec{v}_{21}^A=\vec{v}_{21}^B=\vec{0}$ , el eje instantáneo del movimiento {21} pasa por esos dos puntos, es decir, $\vec{\omega}_{21}=\omega_{21}\,\vec{\imath}_0$ . Pero entonces también pasa en todo instante por el origen de coordenadas, $O 1$ . Podemos decir entonces que el punto $O 1$ es un punto fijo en este movimiento, y por tanto

$\vec{v}_{21}^{O_1}=\vec{0}\qquad\qquad\vec{a}_{21}^{O_1}=\vec{0}$

Usando la ecuación del campo de velocidades, tenemos

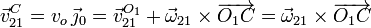
$\vec{v}_{21}^C=v_o\,\vec{\jmath}_0=\vec{v}_{21}^{O_1}+\vec{\omega}_{21}\times\overrightarrow{O_1C}=\vec{\omega}_{21}\times\overrightarrow{O_1C}$

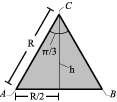
Necesitamos el vector geométrico 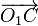$\overrightarrow{O_1C}$ . Si nos fijamos en la figura adjunta, observamos que el triángulo $A B C$ es equilátero, pues la distancia entre los raíles es $R$ , el radio de la esfera. Los tres ángulos son entonces de $π / 3$ radianes, con lo que podemos calcular la altura del triángulo, que es la coordenada $z 0$ del punto $C$ . Obtenemos las coordenadas respecto a $O 1$ en la base vectorial del sólido "0"

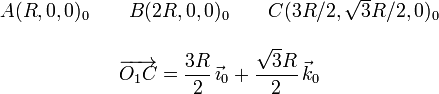
$\begin{array}{c} A(R,0,0)_{0}\qquad B(2R,0,0)_{0}\qquad C(3R/2,\sqrt{3}R/2,0)_{0}\\ \\ \overrightarrow{O_1C}=\dfrac{3R}{2}\,\vec{\imath}_0+\dfrac{\sqrt{3}R}{2}\,\vec{k}_0 \end{array}$

Podemos plantear ahora la ecuación obtenida a partir del campo de velocidades

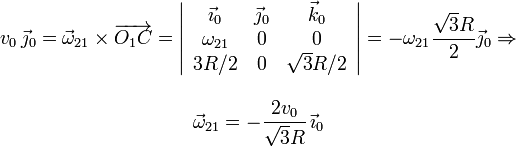
$\begin{array}{c} v_0\,\vec{\jmath}_0 = \vec{\omega}_{21}\times\overrightarrow{O_1C}= \left| \begin{array}{ccc} \vec{\imath}_0&\vec{\jmath}_0&\vec{k}_0\\\omega_{21}&0&0\\3R/2&0&\sqrt{3}R/2 \end{array} \right|=-\omega_{21}\dfrac{\sqrt{3}R}{2}\vec{\jmath}_0\Rightarrow\\ \\ \vec{\omega}_{21}=-\dfrac{2v_0}{\sqrt{3}R}\,\vec{\imath}_0 \end{array}$

La reducción del movimiento {21} en $O 1$ es

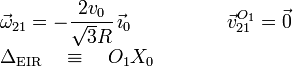
$\begin{array}{lcl} \vec{\omega}_{21}=-\dfrac{2v_0}{\sqrt{3}R}\,\vec{\imath}_0&\qquad& \vec{v}_{21}^{O_1}=\vec{0}\\ \Delta_{\mathrm{EIR}}\quad\equiv\quad O_1X_0&& \end{array}$

2.2 Movimiento {01}

Hemos de calcular la velocidad angular $\vec{\omega}_{01}$ . El punto $O_1</math> es también un punto fijo en {01}, pues pertenece al eje de giro, entonces

$\vec{v}_{01}^{O_1}=\vec{0}\qquad\qquad\vec{a}_{01}^{O_1}=\vec{0}$

Por definición, el sólido "0" se mueve de modo que el punto $C$ esta siempre en el plano $O 1 X 0 Z 0$ . Entonces $C$ es un punto fijo en el movimiento {20}, y por tanto

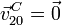
$\vec{v}_{20}^C=\vec{0}$

Ahora bien, usando la regla de composición podemos escribir

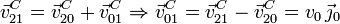
$\vec{v}_{21}^C =\vec{v}_{20}^C+\vec{v}_{01}^C\Rightarrow\vec{v}_{01}^C=\vec{v}_{21}^C-\vec{v}_{20}^C=v_0\,\vec{\jmath}_0$

Pero podemos escribir 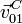$\vec{v}_{01}^C$ usando el campo de velocidades del sólido en el movimiento {01}

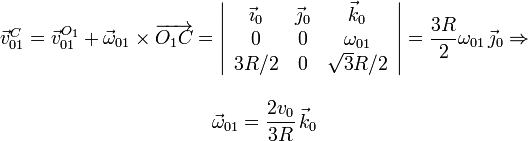
$\begin{array}{c} \vec{v}_{01}^C=\vec{v}_{01}^{O_1}+\vec{\omega}_{01}\times\overrightarrow{O_1C}= \left| \begin{array}{ccc} \vec{\imath}_0&\vec{\jmath}_0&\vec{k}_0\\0&0&\omega_{01}\\3R/2&0&\sqrt{3}R/2 \end{array} \right|=\dfrac{3R}{2}\omega_{01}\,\vec{\jmath}_0\Rightarrow\\ \\ \vec{\omega}_{01}=\dfrac{2v_0}{3R}\,\vec{k}_0 \end{array}$

La reducción de {01} en $O 1$ es

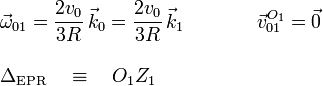
$\begin{array}{lcl} \vec{\omega}_{01}=\dfrac{2v_0}{3R}\,\vec{k}_0=\dfrac{2v_0}{3R}\,\vec{k}_1&\quad\quad& \vec{v}_{01}^{O_1}=\vec{0}\\ &&\\ \Delta_{\mathrm{EPR}}\quad\equiv\quad O_1Z_1&& \end{array}$

2.3 Movimiento {20}

Determinamos la velocidad angular a partir de la composición {20} = {21} + {10}

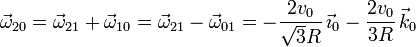
$\vec{\omega}_{20}=\vec{\omega}_{21}+\vec{\omega}_{10}=\vec{\omega}_{21}-\vec{\omega}_{01}= -\dfrac{2v_0}{\sqrt{3}R}\,\vec{\imath}_0-\dfrac{2v_0}{3R}\,\vec{k}_0$

El punto $O 1$ pertenece al eje instantáneo de {21} y {01}. Entonces también pertenece al eje del movimiento {20}. Tenemos

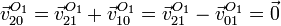
$\vec{v}_{20}^{O_1}=\vec{v}_{21}^{O_1}+\vec{v}_{10}^{O_1}=\vec{v}_{21}^{O_1}-\vec{v}_{01}^{O_1}=\vec{0}$

La reducción en $O 1$ queda

$\begin{array}{lcl} \vec{\omega}_{20} = -\dfrac{2v_0}{\sqrt{3}R}\,\vec{\imath}_0-\dfrac{2v_0}{3R}\,\vec{k}_0 &\qquad& \vec{v}_{20}^{O_1}=\vec{0}\\ &&\\ \Delta_{\mathrm{EIR}}\quad\equiv\quad O_1C\quad\equiv\quad\lambda\,\vec{\omega}_{20} \end{array}$

2.4 Vectores 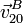$\vec{v}_{20}^B$ y $\vec{a}_{21}^B$

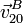
Una vez reducido el movimiento {20} en $C$ , podemos aplicar la ecuación del campo de velocidades de un sólido rígido para calcular $\vec{v}_{20}^B$

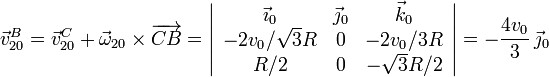
$\vec{v}_{20}^B = \vec{v}_{20}^C+\vec{\omega}_{20}\times\overrightarrow{CB}= \left| \begin{array}{ccc} \vec{\imath}_0&\vec{\jmath}_0&\vec{k}_0\\-2v_0/\sqrt{3}R&0&-2v_0/3R\\R/2&0&-\sqrt{3}R/2 \end{array} \right|=-\dfrac{4v_0}{3}\,\vec{\jmath}_0$

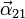Calculamos la aceleración $\vec{a}_{21}^B$ aplicando la ecuación del campo de aceleraciones del movimiento {21} y partiendo del punto fijo de este movimiento, $O 1$ . Necesitamos el vector $\vec{\alpha}_{21}$ . Podemos obtenerlo derivando $\vec{\omega}_{21}$

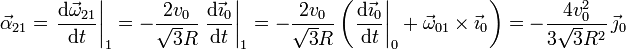
$\vec{\alpha}_{21}=\left.\dfrac{\mathrm{d}\vec{\omega}_{21}}{\mathrm{d}t}\right|_1= -\dfrac{2v_0}{\sqrt{3}R}\left.\dfrac{\mathrm{d}\vec{\imath}_0}{\mathrm{d}t}\right|_1 = -\dfrac{2v_0}{\sqrt{3}R}\left(\left.\dfrac{\mathrm{d} \vec{\imath}_0}{\mathrm{d}t}\right|_0+ \vec{\omega}_{01}\times\vec{\imath}_0\right)= -\dfrac{4v_0^2}{3\sqrt{3}R^2}\,\vec{\jmath}_0$

Con esto podemos calcular el vector pedido

$\vec{a}_{21}^B = \vec{a}_{21}^{O_1}+\vec{\alpha}_{21}\times\overrightarrow{O_1B}+\vec{\omega}_{21}\times(\vec{\omega}_{21}\times\overrightarrow{O_1B})=\dfrac{8v_0^2}{3\sqrt{3}R}\,\vec{k}_0$

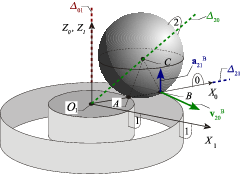
En a figura siguiente se muestran los ejes instantáneos de rotación de los tres movimientos analizados en el problema, así como los dos vectores pedidos.

Esfera sobre dos raíles (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {21}

2.2 Movimiento {01}

2.3 Movimiento {20}

2.4 Vectores $\vec{v}_{20}^B$ y $\vec{a}_{21}^B$

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

Esfera sobre dos raíles (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {21}

2.2 Movimiento {01}

2.3 Movimiento {20}

2.4 Vectores y

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES

2.4 Vectores $\vec{v}_{20}^B$ y $\vec{a}_{21}^B$