Coche sobre una plataforma circular (G.I.A.)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

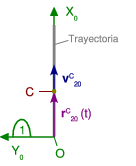
Una plataforma circular gira alrededor de un eje perpendicular a ella que pasa por su centro con velocidad angular uniforme $ω$ . Un coche se mueve radialmente desde el centro de la plataforma hacia fuera con velocidad uniforme $v c$ . Encuentra la expresión de la velocidad del coche visto desde la plataforma y desde un observador en reposo absoluto. Describe las trayectorias que describe el coche para cada uno de estos observadores.

Ayuda

$\begin{array}{ccc} \displaystyle\int t\,\,\mathrm{sen}\,(\omega t)\mathrm{d} t = -\dfrac{t}{\omega}\cos(\omega t) + \dfrac{1}{\omega^2}\,\mathrm{sen}\,(\omega t)& \qquad &\displaystyle\int t\,\cos(\omega t)\mathrm{d} t = \dfrac{t}{\omega}\,\mathrm{sen}\,(\omega t) + \dfrac{1}{\omega^2}\cos(\omega t) \end{array}$

2 Solución

Este problema es similar al anterior. La diferencia es que uno de los sólidos, concretamente la plataforma, está rotando respecto al suelo. Llamamos sólido "1" al suelo. El sólido "0" será la plataforma, mientras que el coche será el sólido "2". Consideramos que el coche es un punto material que identificamos con la letra $C$ .

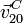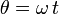Los datos que nos da el problema son la velocidad del coche respecto de la plataforma ( $\vec{v}^C_{20}$ ) y el vector rotación de ésta respecto del suelo ( $\vec{\omega}_{01}$ ). El sistema de ejes del triedro "0" gira solidariamente con la plataforma, de forma que el ángulo es $\theta=\omega\,t$ , pues la velocidad angular es constante en el tiempo. Utilizando la notación del movimiento relativo y los ejes indicados en la figura tenemos

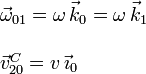
$\left. \begin{array}{l} \vec{\omega}_{01} = \omega\,\vec{k}_0 = \omega\,\vec{k}_1 \\ \\ \vec{v}^C_{20} = v\,\vec{\imath}_0 \end{array} \right.$

\picskip{0} Vamos a analizar los movimientos elementales del problema.

2.1 Movimiento {01}

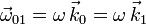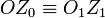Este es el movimiento de la plataforma respecto del suelo. Es una rotación permanente con $\vec{\omega}_{01}=\omega\,\vec{k}_0=\omega\,\vec{k}_1$ . Hemos de identificar un punto del sólido "0" del cuya velocidad respecto al triedro "1" sea fácil de determinar. Lo más sencillo es escoger un punto del eje de rotación. Aquí, el eje permanente de rotación del movimiento {01} es el eje $OZ_0\equiv O_1Z_1$ . Entonces el punto 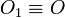$O_1\equiv O$ pertenece al eje. La reducción en $O$ es

$\vec{v}^O_{01} = \vec{0} \qquad \qquad \vec{\omega}_{01} = \omega\,\vec{k}_0$

A partir de esta reducción podemos determinar la velocidad de cualquier punto del sólido "0" respecto del "1" utilizando la ecuación del campo de velocidades del movimiento {01}

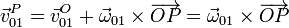
$\vec{v}^P_{01} = \vec{v}^O_{01} + \vec{\omega}_{01}\times\overrightarrow{OP} =\vec{\omega}_{01}\times\overrightarrow{OP}$

2.2 Movimiento {20}

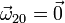Este es el movimiento del coche respecto a la plataforma. Es una traslación, por lo que $\vec{\omega}_{20}=\vec{0}$ . Al ser una traslación la velocidad es la misma en todos los puntos del sólido. La reducción en cualquier punto es

$\vec{v}_{20} = v\,\vec{\imath}_0 \qquad\qquad \vec{\omega}_{20}=\vec{0}$

2.3 Movimiento {21}

Este es el movimiento del coche respecto al suelo. Lo describimos como composición de los dos movimientos anteriores.

{21} = {20} + {01}

La ley de composición de velocidades angulares es

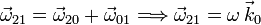
$\vec{\omega}_{21} = \vec{\omega}_{20} + \vec{\omega}_{01} \Longrightarrow \vec{\omega}_{21} = \omega\,\vec{k}_0$

Aplicando la ley de composición de velocidades resulta

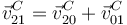
$\vec{v}^C_{21} = \vec{v}^C_{20} + \vec{v}^C_{01}$

Como {20} es una traslación, tenemos

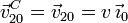
$\vec{v}^C_{20} = \vec{v}_{20} = v\,\vec{\imath}_0$

Usando la ecuación del campo de velocidades de {01} tenemos

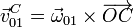
$\vec{v}^C_{01} = \vec{\omega}_{01}\times\overrightarrow{OC}$

Como vemos en la figura, el vector $\overrightarrow{OC}$ es

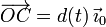
$\overrightarrow{OC} = d(t) \,\vec{\imath}_0$

donde $d (t)$ es la distancia recorrida por el coche sobre el eje $O X 0$ . Como el módulo de la velocidad es constante tenemos 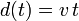$d(t) = v\,t$ . Nos queda

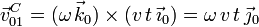
$\vec{v}^C_{01} = (\omega\,\vec{k}_0)\times(v\,t\,\vec{\imath}_0) = \omega\,v\,t\,\vec{\jmath}_0$

Así pues, la velocidad buscada es

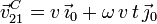
$\vec{v}^C_{21} = v\,\vec{\imath}_0 +\omega\, v\,t\,\vec{\jmath}_0$

Observamos que 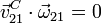$\vec{v}^C_{21}\cdot\vec{\omega}_{21}=0$ . Es decir, el movimiento {21} es una rotación pura, pues el vector rotación es no nulo y perpendicular a la velocidad en $C$ (y por tanto a la velocidad en cualquier punto del sólido "2"). Podemos preguntarnos por al posición del EIR de este movimiento. Para determinar un punto del eje vamos a partir de la velocidad en el punto $O$ , pues es más fácil de visualizar. Aplicando la composición de movimientos tenemos

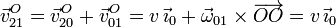
$\vec{v}^O_{21} = \vec{v}^O_{20} + \vec{v}^O_{01} = v\,\vec{\imath}_0 + \vec{\omega}_{01}\times\overrightarrow{OO} = v\,\vec{\imath}_0$

Es interesante recalcar que el punto $O$ del sólido "2" se mueve respecto al "1". Determinamos la posición respecto a $O$ de un punto del EIR

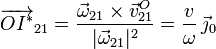
$\overrightarrow{OI^*}_{21} = \dfrac{\vec{\omega}_{21}\times\vec{v}^O_{21}}{|\vec{\omega}_{21}|^2} = \dfrac{v}{\omega}\,\vec{\jmath}_0$

La ecuación vectorial del eje es

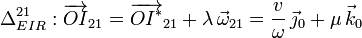
$\Delta^{21}_{EIR} : \overrightarrow{OI}_{21} = \overrightarrow{OI^*}_{21} + \lambda\,\vec{\omega}_{21} = \dfrac{v}{\omega}\,\vec{\jmath}_0 + \mu\,\vec{k}_0$

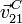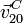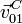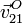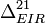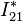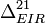La figura muestra la velocidad $\vec{v}^C_{21}$ como suma de $\vec{v}^C_{20}$ y $\vec{v}^C_{01}$ , así como la velocidad $\vec{v}^O_{21}$ y la posición de $\Delta^{21}_{EIR}$ . Como en cada instante es una rotación, las velocidad en cada punto debe ser perpendicular a la línea que une el punto con el EIR, como indica la línea de puntos que une el punto $C$ con el punto $I^*_{21}$ de la recta $\Delta^{21}_{EIR}$ .

2.4 Trayectorias del coche para cada observador

Para encontrar la ecuación de la trayectoria vista por un observador en el suelo (sólido "1" ) y en la plataforma (sólido "0") hay que encontrar el vector de posición del coche en cada uno de esos sistemas.

2.4.1 Trayectoria desde la plataforma

El vector de posición se obtiene integrando la velocidad vista desde el sistema "0". Tenemos

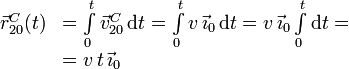
$\begin{array}{ll} \vec{r}^C_{20}(t)& = \int\limits_0^t \vec{v}^C_{20}\,\mathrm{d} t = \int\limits_0^t v\,\vec{\imath}_0\,\mathrm{d} t= v\,\vec{\imath}_0\int\limits_0^t\mathrm{d} t=\\ &=v\,t\,\vec{\imath}_0 \end{array}$

Hemos expresado la velocidad en la base del sólido "0", el sólido observador en este caso. El vector de la base 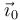$\vec{\imath}_0$ puede salir de la integral porque desde el punto de vista del triedro "0" es constante en el tiempo. Hemos supuesto que en $t = 0$ el coche estaba en el punto $O$ (en el centro de la plataforma). La ecuación paramétrica de la trayectoria es

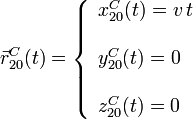
$\vec{r}^C_{20}(t) = \left\{ \begin{array}{l} x^C_{20}(t) = v\,t \\ \\ y^C_{20}(t) = 0 \\ \\ z^C_{20}(t) = 0 \end{array} \right.$

La trayectoria es una recta que coincide con el eje $O X 0$ .

2.4.2 Trayectoria desde el suelo

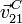El vector de posición se obtiene integrando la velocidad vista desde el sistema "1". Para ello hay que expresar la velocidad $\vec{v}^C_{21}$ en términos de la base del triedro "1". A partir de la primera figura vemos que

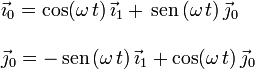
$\left. \begin{array}{l} \vec{\imath}_0 = \cos(\omega\,t)\,\vec{\imath}_1 + \,\mathrm{sen}\,(\omega \,t)\,\vec{\jmath}_0 \\ \\ \vec{\jmath}_0 = -\,\mathrm{sen}\,(\omega\,t)\,\vec{\imath}_1 + \cos(\omega \,t)\,\vec{\jmath}_0 \end{array} \right.$

Es decir, la velocidad 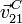$\vec{v}^C_{21}$ puede escribirse

$\vec{v}^C_{21} = [v\,\cos(\omega\,t)-\omega\,v\,t\,\,\mathrm{sen}\,(\omega\,t)]\,\vec{\imath}_1 + [v\,\,\mathrm{sen}\,(\omega\,t)+\omega\,v\,t\,\cos(\omega\,t)]\,\vec{\jmath}_1$

El vector de posición respecto al triedro "1" es

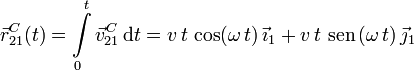
$\vec{r}^C_{21}(t) = \int\limits_0^t \vec{v}^C_{21}\,\mathrm{d} t = v\,t\,\cos(\omega\,t)\,\vec{\imath}_1 + v\,t\,\,\mathrm{sen}\,(\omega\,t)\,\vec{\jmath}_1$

Hemos utilizado las integrales dadas en el enunciado. Desde el punto de vista del triedro "1" los vectores de la base no cambian en el tiempo y pueden salir de la integral. También hemos supuesto que en $t = 0$ el coche estaba en el punto $O 1$ . La ecuación paramétrica de la trayectoria es

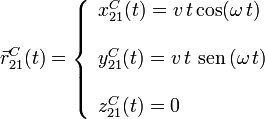
$\vec{r}^C_{21}(t) = \left\{ \begin{array}{l} x^C_{21}(t) = v\,t\cos(\omega\,t) \\ \\ y^C_{21}(t) = v\,t\,\,\mathrm{sen}\,(\omega\,t) \\ \\ z^C_{21}(t) = 0 \end{array} \right.$

Esta es la ecuación de una espiral, que se muestra en la figura.

Coche sobre una plataforma circular (G.I.A.)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Movimiento {01}

2.2 Movimiento {20}

2.3 Movimiento {21}

2.4 Trayectorias del coche para cada observador

2.4.1 Trayectoria desde la plataforma

2.4.2 Trayectoria desde el suelo

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES