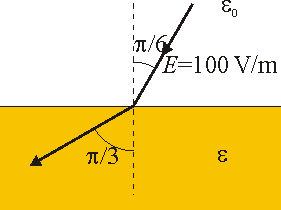Problemas de materiales dieléctricos
De Laplace
| Línea 129: | Línea 129: | ||
===[[Condensador esférico relleno parcialmente de dieléctrico]]=== | ===[[Condensador esférico relleno parcialmente de dieléctrico]]=== | ||
| - | Se tiene un condensador esférico, formado por dos superficies metálicas de radios <math>a</math> y <math>b</math>. Para mantenerla en su posición, la esfera central está sujeta por dos cuñas dieléctricas sólidas, de permitividad <math>\varepsilon_1</math>. Las cuñas tienen forma de sectores esféricos, valiendo el semiángulo <math>\theta_0=\pi/3</math> para las dos cuñas. El resto del espacio entre las esferas queda vacío. | + | Se tiene un condensador esférico, formado por dos superficies metálicas de radios <math>a</math> y <math>b</math>. Para mantenerla en su posición, la esfera central está sujeta por dos cuñas dieléctricas sólidas, de permitividad <math>\varepsilon_1</math>. Las cuñas tienen forma de sectores esféricos, valiendo el semiángulo <math>\theta_0=\pi/3\,</math> para las dos cuñas. El resto del espacio entre las esferas queda vacío. |
Halle la capacidad de este condensador. | Halle la capacidad de este condensador. | ||
<center>[[Imagen:Esferaconos.gif]]</center> | <center>[[Imagen:Esferaconos.gif]]</center> | ||
| + | |||
| + | [[Condensador esférico relleno parcialmente de dieléctrico|'''Solución''']] | ||
===[[Esfera dieléctrica en un campo externo]]=== | ===[[Esfera dieléctrica en un campo externo]]=== | ||
Revisión de 18:49 25 jun 2008
1 Permitividad de un gas noble
El estudio de las propiedades dieléctricas de los gases puede servir para medir el tamaño de los átomos.
Para ello, suponga que se modela un átomo de número atómico Z como compuesto de una carga puntual Ze (el núcleo) y una nube esférica uniforme, con volumen τ (los electrones). Si a un átomo de este tipo se le aplica un campo externo uniforme 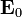 , ¿cuánto vale el momento dipolar inducido en el átomo por la separación de los centros de carga?
, ¿cuánto vale el momento dipolar inducido en el átomo por la separación de los centros de carga?
Para un gas monoatómico (un gas noble) con una densidad de N átomos por unidad de volumen, ¿cuánto valdrá la susceptibilidad y la permitividad?
Experimentalmente se comprueba que el helio en condiciones normales tiene una permitividad relativa 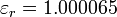 , mientras que para el neón
, mientras que para el neón 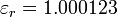 , y para el argón
, y para el argón  . Según esto, ¿cuál es el tamaño de un átomo de cada uno de estos gases nobles?
. Según esto, ¿cuál es el tamaño de un átomo de cada uno de estos gases nobles?
2 Esfera polarizada uniformemente
Se tiene una esfera dieléctrica de radio R polarizada uniformemente con .
.
- Halle, por integración directa el potencial eléctrico en todos los puntos del espacio.
- ¿Cuáles son los valores de
 ,
,  y
y  dentro y fuera de la esfera?
dentro y fuera de la esfera?
- ¿Cuánto valen las densidades de carga equivalentes a la polarización?
3 Medio polarizado entre dos placas
Entre dos placas metálicas planas y paralelas, de sección S y separadas una distancia a, se encuentra un dieléctrico que presenta polarización remanente, de forma que en él

siendo 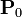 un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
un vector uniforme, en la dirección perpendicular a las placas. El dieléctrico es perfectamente aislante.
- Inicialmente las placas están descargadas. Si se conectan mediante un voltímetro, ¿cuánto medirá éste?
- Suponga que las dos placas se conectan mediante un hilo conductor, ¿cuánta carga se almacena en cada placa metálica?
- Calcule cómo cambian los resultados si la polarización del dieléctrico no es constante, sino que depende del campo como
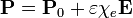
4 Esfera polarizada radialmente
Se tiene una esfera de radio R, centrada en el origen, compuesta de un material con una polarización radial
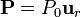
- Calcule la distribución de cargas equivalente a esta polarización.
- Determine los campos
 y
y  en todo el espacio.
en todo el espacio.
5 Condensador con dos capas de dieléctrico
Entre dos placas metálicas conductoras planas y paralelas a una distancia d = a + b se colocan dos dieléctricos de permitividades 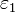 y
y 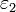 y espesores a y b respectivamente, tal como muestra la figura. Halle la capacidad de este condensador y construya el circuito equivalente.
y espesores a y b respectivamente, tal como muestra la figura. Halle la capacidad de este condensador y construya el circuito equivalente.

6 Condensador con dos y con cuatro bloques de dieléctrico
Repita el problema de dos dieléctricos entre dos placas suponiendo que la interfaz que separa los dieléctricos es perpendicular a las placas.
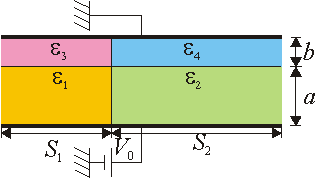
¿Se podría resolver un problema similar pero con cuatro dieléctricos, tal como muestra la figura? ¿Cuál sería el circuito equivalente?
7 Refracción de un campo eléctrico
El campo eléctrico en el exterior de un dieléctrico tiene por módulo 100 V/m y forma un ángulo π / 6 con la normal a la superficie. El campo en el interior del medio forma un ángulo π / 3 con la normal. Halle:- La permitividad relativa del medio.
- El módulo del campo en el interior del material.
- La densidad de carga de polarización en la frontera.
- El salto en la componente tangencial de
 .
.
8 Ruptura dieléctrica
La ruptura dieléctrica se produce cuando el campo eléctrico entre dos conductores supera un valor crítico, saltando una chispa en el vacío, o quemando el dieléctrico que pueda haber en medio.
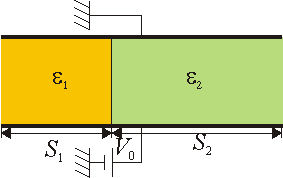
Una situación en la que puede producirse la ruptura es la siguiente. Suponga dos placas metálicas planas de sección S situadas paralelamente a una distancia a una de la otra. La placa inferior se encuentra a tierra y la superior a un potencial V0.
- Sobre la placa inferior se encuentra depositada una chapa (que podemos suponer plana y de espesor despreciable) de sección S0. Halle la carga que se deposita en la chapa.
- Suponga que esta chapa se separa de la placa inferior, quedándose aislada, y se acerca a la superior (manteniéndose siempre paralela a ambas). Cuando se halla a una distancia x de la placa inferior, ¿cuál es su tensión? ¿Cuánto vale el campo eléctrico entre la chapa y la placa superior?
- Si el campo para que se produzca la chispa es E0, ¿cuál es la posición x en la cual se produce la chispa?
- Cuando se produce la chispa, la tensión de la chapa pasa a ser V0, ¿cuánto varía en ese proceso la carga almacenada en la chapa? ¿Y la carga almacenada en la placa superior?
Desprecie los efectos de borde.
9 Corteza polarizada radialmente
Una corteza esférica de radio interior a y exterior b está hecha de dieléctrico polarizado según la ley
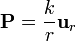
No hay más cargas en el sistema
- Calcule las densidades de carga de polarización en el sistema. ¿Cuánto vale la carga total de polarización?
- Halle los campos
 y
y  en todo el espacio.
en todo el espacio.
- Determine el valor del potencial eléctrico en todo el espacio.
10 Microtira situada entre dos placas
Sobre una placa metálica plana, de sección S (que supondremos en z = 0), se coloca una capa de dieléctrico de permitividad 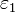 con espesor a. Sobre esta capa se sitúa
una lámina metálica, de sección S0 < S, el resto de la superficie se deja libre y descargado. Se superpone una segunda capa de dieléctrico de permitividad
con espesor a. Sobre esta capa se sitúa
una lámina metálica, de sección S0 < S, el resto de la superficie se deja libre y descargado. Se superpone una segunda capa de dieléctrico de permitividad 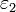 y espesor b. Por último, el sistema se cierra con una segunda lámina metálica de sección S.
y espesor b. Por último, el sistema se cierra con una segunda lámina metálica de sección S.
Si las placas inferior, intermedia y superior se colocan, respectivamente, a potenciales V1, V2 y V3, ¿Cuánto vale la carga (libre) almacenada en cada conductor? Desprecie totalmente los
efectos de borde (suponiendo 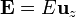 ) y los posibles campos exteriores al sistema.
) y los posibles campos exteriores al sistema.
11 Condensador relleno de un medio estratificado
Un medio estratificado es aquel cuyas propiedades dependen de la altura z. Un material de este tipo se coloca entre dos placas conductoras planas y paralelas, separadas una distancia a. La permitividad del material varía de 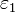 a
a 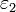 en
la forma
en
la forma
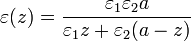
Si se aplica una diferencia de potencial V0 entre las placas,
- ¿Cuánto valen los campos
 ,
,  y
y  en todos los puntos del material?
en todos los puntos del material?
- ¿Cuál es la densidad de carga de polarización (tanto superficial como de volumen)?
- Halle la energía almacenada en el sistema
Desprecie los efectos de borde.
12 Energía en un condensador con y sin dieléctrico
El espacio entre dos placas metálicas circulares de 26 cm de diámetro, situadas paralelamente a una distancia 2 mm está vacío.
Entre las placas se establece una diferencia de potencial de 20 V
- ¿Cuánto vale la energía almacenada en el sistema?
- Suponga que, una vez cargado el condensador se desconecta la fuente y se introduce entre las placas una lámina de metacrilato (
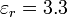 ) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
) de 2 mm de espesor. ¿Cuánto cambia la energía almacenada en el sistema? ¿Cómo se explica la diferencia?
- Suponiendo que el proceso anterior se hubiera efectuado sin desconectar la fuente, ¿cuál sería en ese caso la variación en la energía? ¿Cuánto trabajo realizaría la fuente de tensión?
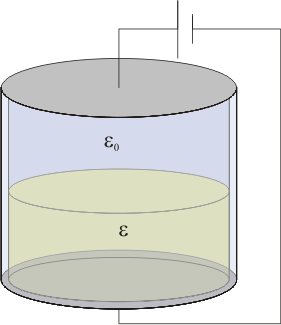
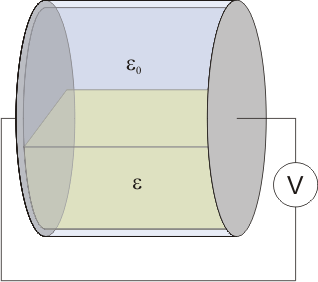
13 Recipiente lleno hasta la mitad de dieléctrico
Se construye un recipiente cilíndrico, con bases perfectamente conductoras de sección S, separadas una distancia a, y paredes perfectamente dieléctricas, de espesor despreciable. El interior se llena hasta la mitad con un líquido dieléctrico y permitividad . El resto se deja vacío.
. El resto se deja vacío.
El recipiente se coloca en un principio con las bases dispuestas horizontalmente. En esta posición, se carga hasta que la diferencia de potencial entre las placas es V0. Acto seguido se abre el circuito y, sin descargar las placas, el recipiente es girado 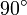 alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
alrededor de un eje horizontal. ¿Cuál es la nueva diferencia de potencial entre las placas? ¿Cómo varía la energía almacenada?
Desprecie los efectos de borde y la influencia de las paredes.
14 Condensador esférico relleno parcialmente de dieléctrico
Se tiene un condensador esférico, formado por dos superficies metálicas de radios a y b. Para mantenerla en su posición, la esfera central está sujeta por dos cuñas dieléctricas sólidas, de permitividad 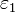 . Las cuñas tienen forma de sectores esféricos, valiendo el semiángulo
. Las cuñas tienen forma de sectores esféricos, valiendo el semiángulo 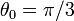 para las dos cuñas. El resto del espacio entre las esferas queda vacío.
para las dos cuñas. El resto del espacio entre las esferas queda vacío.
Halle la capacidad de este condensador.

15 Esfera dieléctrica en un campo externo
Supóngase que se tiene una esfera de radio R un material dieléctrico (de permitividad  ) alrededor de la cual hay vacío. En puntos alejados de la esfera hay impuesto un campo eléctrico uniforme
) alrededor de la cual hay vacío. En puntos alejados de la esfera hay impuesto un campo eléctrico uniforme 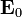 . Halle el potencial y el campo eléctrico en el interior y el exterior de la esfera.
. Halle el potencial y el campo eléctrico en el interior y el exterior de la esfera.
Sugerencia: El campo eléctrico dentro de la esfera es uniforme. Sabiendo esto, aplique el resultado conocido para dicho caso.
16 Energía en una esfera conductora con dieléctrico
Una esfera metálica de radio R se encuentra aislada y almacena una carga Q. La esfera se encuentra en el vacío.
- Indique la energía almacenada en el sistema
- Suponga que, sin descargar la esfera, esta se recubre con una capa de espesor $a$ de un dieléctrico de permitividad
 . Determine la nueva energía almacenada en el sistema. ¿Cómo se explica el cambio en la energía?
. Determine la nueva energía almacenada en el sistema. ¿Cómo se explica el cambio en la energía?
- Si en lugar de una esfera aislada y descargada tenemos una esfera conectada a un generador que fija su potencial en un valor V0, ¿cuál es la energía antes y después del recubrimiento? ¿Cómo se interpreta el cambio en este caso?
17 Fuerza entre conductores con dieléctricos entre ellos
En un sistema formado por dos esferas metálicas concéntricas de radios $a$ y $c$, entre las cuales se encuentran dos medios dieléctricos, con una interfaz ecuatorial, existe una fuerza de atracción entre los electrodos, que está ausente si solo hay un medio dieléctrico que llene todo el espacio entre las placas. Se trata de calcular esta fuerza.
- Determine la densidad de carga libre en la superficie del electrodo interior.
- Halle el valor del campo eléctrico en los mismos puntos.
- La fuerza sobre un elemento de superficie conductora es
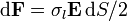 . Integrando esta fuerza elemental, determine la fuerza neta sobre el electrodo interior. ¿Hacia donde va dirigida? ¿Cuál es el origen de esta fuerza?
. Integrando esta fuerza elemental, determine la fuerza neta sobre el electrodo interior. ¿Hacia donde va dirigida? ¿Cuál es el origen de esta fuerza?
- De forma análoga, calcule la fuerza sobre el electrodo exterior. ¿Se verifica la tercera ley de Newton?