Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática del movimiento rectilíneo (GIOI)

De Laplace

Contenido

1 Posición dependiente del tiempo

Una partícula se mueve de manera que su posición como función del tiempo está representada en la gráfica de la figura

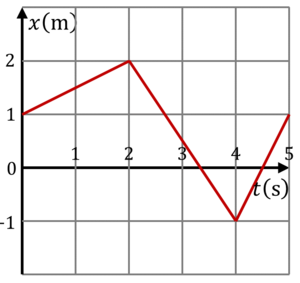
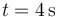  1. ¿Cuánto vale su desplazamiento entre t=0 \,\mathrm{s} y t=4 \,\mathrm{s} ?
  2. ¿Cuánto vale la distancia total recorrida en el mismo intervalo?
  3. ¿Cuánto vale el desplazamiento y la distancia total recorrida en el intervalo (0 s,5 s)?
  4. ¿Cuánto vale la velocidad media en los intervalos (0 s,5 s), (0 s,4 s) y (2 s,5 s)?
  5. ¿Cómo es la gráfica de la velocidad instantánea como función del tiempo?

Solución

2 Persecución policial

Las especificaciones del Land Rover Discovery establecen que va de 0 a 100 km/h en 8.7s. ¿Cuánto vale su aceleración media en este periodo? ¿Cuánto vale el tiempo mínimo para atravesar un cruce de 15 m de anchura, si parte de estar parado en un semáforo? ¿Con qué velocidad llegará al otro lado?

Un Seat León FR amarillo circula por la carretera a 160 km/h y pasa junto a un coche de la Guardia Civil parado en el arcén. Sabiendo que la benemérita usa un Land Rover Discovery, ¿cuál es el mínimo tiempo que tarda en alcanzar al Seat León si este no reduce su velocidad? ¿A qué distancia del punto donde estaba parado lo alcanza? ¿Qué velocidad tiene el coche patrulla en el momento en que alcanza al infractor?

Solución

3 Piedra y pájaro que se mueven verticalmente

Desde un punto a una altura 1.4 m respecto al suelo, un niño lanza verticalmente una piedra contra un pájaro que está 1.6 m más arriba. La velocidad inicial de la piedra es de 7.0 m/s. Tal como lanza la piedra, el pájaro sale volando hacia arriba con velocidad constante v1.

Despreciando el rozamiento del aire sobre la piedra y tomando g = 9.8 m/s²:

  1. Calcule el máximo valor de v1 con que asciende el pájaro, si la piedra es capaz de alcanzarle.
  2. Suponiendo que ha volado con esta velocidad máxima, calcule la velocidad instantánea de la piedra y del pájaro en el momento del impacto, así como la velocidad media de cada uno desde el lanzamiento hasta ese momento.
  3. Si en lugar de darle la piedra falla por poco y continúa su vuelo, ¿hasta que altura respecto al suelo llega? ¿Qué velocidad tiene cuando impacta de nuevo con el suelo?

Solución

4 Rapidez de impacto

Una partícula está sometida exclusivamente a la acción de la gravedad. Si se lanza con velocidad + v0 en dirección vertical hacia arriba desde un punto de altura h. ¿Cuál es su velocidad cuando llega al suelo? Si en vez de lanzarse hacia arriba se lanza hacia abajo, con velocidad − v0, ¿llegará con una rapidez mayor?

Solución

5 Análisis numérico de movimiento

La posición de una partícula en distintos instantes de tiempo es, aproximadamente

t (s) 0.0 0.1 0.2 0.3 0.4 0.5 0.6
x (m) −1.728 −0.440 0.560 1.296 1.792 2.072 2.160


t (s) 0.7 0.8 0.9 1.0 1.1 1.2 1.3
x (m) 2.080 1.856 1.512 1.072 0.560 0.000 −0.584


t (s) 1.4 1.5 1.6 1.7 1.8 1.9 2.0
x (m) −1.168 −1.728 −2.240 −2.680 −3.024 −3.248 −3.328

Para este movimiento, halle:

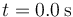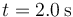  1. El desplazamiento entre t = 0.0\,\mathrm{s} y t=2.0\,\mathrm{s}, así como el valor aproximado de la distancia recorrida en dicho intervalo.
  2. La velocidad media y la rapidez media en el intervalo anterior.
  3. La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
  4. El valor aproximado de la velocidad en t= 1.2\,\mathrm{s}.
  5. El valor aproximado de la aceleración en t= 1.2\,\mathrm{s}.
  6. Sabiendo que este movimiento sigue una ley de la forma
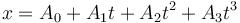
x = A_0 + A_1 t + A_2 t^2 + A_3 t^3\,
Calcule
  1. Los valores de las constantes Ak.
  2. El valor exacto de la distancia recorrida y la rapidez media.
  3. El valor exacto de la velocidad y de la aceleración en t = 1.2\,\mathrm{s}.

Solución

6 Calculo de magnitudes a partir de v(t)

Una partícula se mueve a lo largo de una recta de forma que su velocidad sigue la ley, en el SI

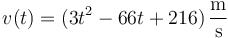
v(t) = (3t^2-66t+216)\,\frac{\mathrm{m}}{\mathrm{s}}

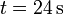entre t=0\,\mathrm{s} y t=24\,\mathrm{s}. La posición inicial es x(0) = 0\,\mathrm{m}. Halle:

  1. La posición de la partícula en cada instante del intervalo indicado.
  2. La velocidad media de la partícula en este intervalo.
  3. Los valores máximo y mínimo de x.
  4. La distancia recorrida en ese intervalo y la rapidez media.
  5. Los valores máximo y mínimo de la velocidad y la rapidez.
  6. La aceleración en todo instante.

Solución

7 Calculo gráfico de velocidad media

La velocidad de una partícula en un movimiento rectilíneo sigue aproximadamente la gráfica de la figura cuando se representa frente al tiempo.

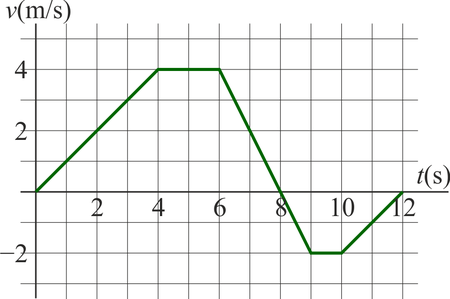
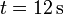  1. ¿Cuánto vale aproximadamente la velocidad media entre t=0\,\mathrm{s} y t=12\,\mathrm{s}?
  2. ¿Cuánto vale la distancia total recorrida por la partícula en el mismo intervalo?
  3. De los cuatro instantes siguientes, ¿en cual la aceleración tiene el mayor valor absoluto? (a) 0.0 s; (b) 5.0 s; (c) 8.0 s; (d) 9.5 s.

Solución

8 Velocidad dependiente del tiempo

Una partícula describe un movimiento rectilíneo cuya velocidad, como función del tiempo entre t=0\,\mathrm{s} y t=10\,\mathrm{s} es la parábola de la figura.

  1. ¿Cuánto vale, aproximadamente, el desplazamiento neto en el intervalo [0s, 10s]?
  2. ¿Cómo es la gráfica de la aceleración de la partícula?
  3. ¿En qué intervalos, en s, la partícula está frenando?
  4. ¿Cuánto vale, aproximadamente, la rapidez media en el intervalo [0s, 10s]?

Solución

9 Aceleración lineal con el tiempo

Una partícula de masa 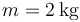m=2\,\mathrm{kg} describe un movimiento rectilíneo en el que la aceleración, como función del tiempo sigue la gráfica de la figura. La partícula parte en t=0\,\mathrm{s} del reposo en x = 0.

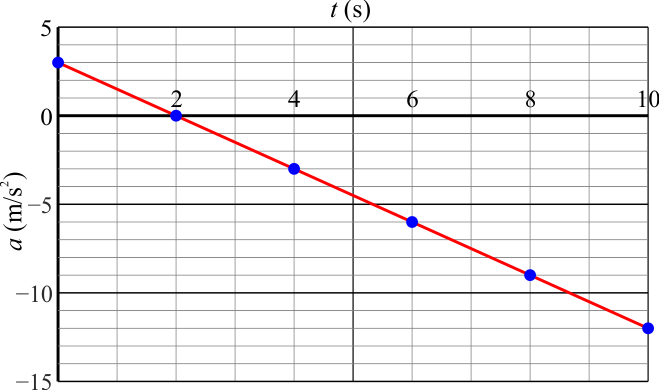
Archivo:Aceleracion-lineal-t.png
  1. ¿Cuánto vale la rapidez de la partícula en t=10\,\mathrm{s}?
  2. ¿Cuál es su velocidad media entre t=0\,\mathrm{s} y t=10\,\mathrm{s}?
  3. ¿Cuál es la distancia total recorrida entre t=0\,\mathrm{s} y t=10\,\mathrm{s}?
  4. ¿Cuánto vale la rapidez media en dicho intervalo?

Solución

10 Velocidad función de la posición

La velocidad de una partícula sigue la ley

v = \sqrt{Ax}

siendo x la distancia recorrida desde el instante inicial.

Calcule la aceleración de la partícula. ¿Qué tipo de movimiento describe?

Solución

11 Velocidad decreciente con la posición

Mediante una serie de sensores se mide la velocidad de un vehículo en puntos equiespaciados, obteniéndose la tabla

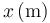
x\,(\mathrm{m}) 0.0 100.0 200.0 300.0 400.0 500.0
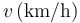
v\,(\mathrm{km}/\mathrm{h}) 108 90 72 54 36 18
  1. ¿Qué ley sencilla cumple la velocidad como función de la posición?
  2. Determine la aceleración como función de x. ¿Se trata de un movimiento uniformemente acelerado?
  3. Halle el valor de la aceleración en cada uno de los puntos de medida.
  4. Calcule el tiempo empleado en recorrer los 500 m. Si continúa con este movimiento, ¿cuánto tardará en recorrer 600 m?

Solución

12 Frenado de un fórmula 1

Cuando el Ferrari de Sebastian Vettel se acerca a la chicane de Monza, su velocidad a 150 m de ésta es de 288 km/h. Cuando entra en la chicane va a 72 km/h.

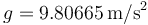  1. Suponiendo que la aceleración es constante, determine su valor. Exprese el resultado en el SI y como un múltiplo de g (siendo g=9.80665\,\mathrm{m}/\mathrm{s}^2).
  2. Determine la velocidad como función de la posición y represéntela gráficamente.
  3. Si el McLaren de Fernando Alonso va a 180 km/h a 150m de la chicane y se detiene a 50m de ésta, ¿es su aceleración mayor o menor que la de Vettel, en valor absoluto?

Solución

13 Cálculo de velocidad media

Una partícula describe un movimiento rectilíneo tal que su velocidad instantánea cumple la ley

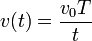
v(t) = \frac{v_0T}{t}

¿Cuánto vale la velocidad media entre t = T y t = 3T?

Solución

14 Velocidad media en un MAS

Una partícula describe un movimiento armónico simple de frecuencia angular ω, pudiéndose mover a lo largo de una recta horizontal. En t = 0 pasa por la posición de equilibrio con una velocidad + v0.

  1. ¿Cuánto vale la velocidad media entre t = 0 y t = T / 4, con T el periodo de oscilación?
  2. ¿Cuánto vale la aceleración en t = T / 4?

Solución

15 Velocidad cuadrática con la posición

Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto v = − kx2. Su posición inicial es x(t = 0) = x0

  1. ¿Cuáles son las unidades de k en el SI
  2. ¿Cuánto vale la aceleración de la partícula cuando se halla en un punto x?
  3. ¿Cuánto vale la posición como función del tiempo?

Solución

16 Velocidad inversamente proporcional a con la posición

En un movimiento rectilíneo, la velocidad de una partícula sigue la ley como función de la posición v = K / x. Inicialmente se encuentra en x0. ¿Qué ley sigue la posición como función del tiempo?

Solución

17 Aceleración dependiente de la posición

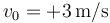Una partícula se mueve sobre una recta partiendo desde x_0=-5\,\mathrm{m} con velocidad v_0=+3\,\mathrm{m}/\mathrm{s}. En su movimiento, experimenta la aceleración

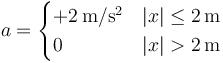
a=\begin{cases}+2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}
  1. ¿Qué velocidad tiene cuando llega al punto x=+7\,\mathrm{m}?
  2. ¿Cuál es la velocidad media en todo el trayecto?
  3. Indique cómo cambian los resultados de los dos apartados anteriores si la aceleración es de la forma
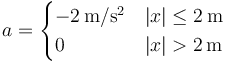
a=\begin{cases}-2\,\mathrm{m}/\mathrm{s}^2 & |x| \leq 2\,\mathrm{m} \\ 0 & |x| > 2\,\mathrm{m}\end{cases}

Solución

18 Caso particular de MAS

Un oscilador armónico con posición de equilibrio xeq = 0 se mueve de tal forma que en 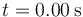t=0.00\,\mathrm{s} la partícula se halla en 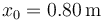x_0=0.80\,\mathrm{m}, moviéndose con velocidad 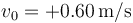v_0=+0.60\,\mathrm{m}/\mathrm{s} y aceleración 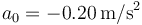a_0=-0.20\,\mathrm{m}/\mathrm{s}^2. Halle la frecuencia ω y el periodo del movimiento, su amplitud de oscilación y la fase inicial. Exprese los fasores (amplitudes complejas) de la posición, velocidad y aceleración.

Solución

19 Otro caso particular de MAS

Una partícula describe el movimiento armónico simple de ecuación horaria, en el SI,

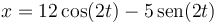
x = 12\cos(2t)-5\,\mathrm{sen}(2t)
  1. ¿Cuanto vale la amplitud de las oscilaciones?
  2. ¿Cuánto vale la velocidad inicial?
  3. ¿Cuánto vale la fase inicial?

Solución

20 Movimiento sinusoidal cuadrático

Una partícula oscila según la ley

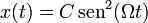
x(t) = C\,\mathrm{sen}^2(\Omega t)
  1. Pruebe que se trata de un movimiento armónico simple. ¿Cuál es su posición de equilibrio?
  2. ¿Cuánto valen la frecuencia, periodo y amplitud de este movimiento?

Solución

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_del_movimiento_rectil%C3%ADneo_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 03:15, 18 feb 2006. - Esta página ha sido visitada 3.005 veces. - Aviso legal - Acerca de Laplace