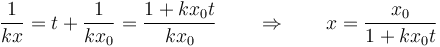Velocidad cuadrática con la posición (GIOI)
De Laplace
Contenido |
1 Enunciado
Una partícula se mueve a lo largo de una recta, de forma que su velocidad vale en cada punto v = − kx2. Su posición inicial es x(t = 0) = x0
- ¿Cuáles son las unidades de k en el SI
- ¿Cuánto vale la aceleración de la partícula cuando se halla en un punto x?
- ¿Cuánto vale la posición como función del tiempo?
2 Unidades de k
Por homogeneidad dimensional
![1\,\frac{\mathrm{m}}{\mathrm{s}}=[k]\left(1\,\mathrm{m}\right)^2 \qquad\Rightarrow\qquad [k]=\frac{1}{\mathrm{m}\cdot\mathrm{s}}](/wiki/images/math/0/c/7/0c7b758a059da01ae14042ac126f4f04.png)
3 Aceleración como función de la posición
Derivamos respecto al tiempo la velocidad, mediante la regla de la cadena
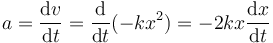
pero la derivada de la posición respecto al tiempo es la propia velocidad
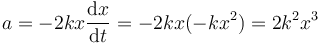
4 Posición como función del tiempo
La velocidad es el cociente entre un desplazamiento diferencial y el intervalo que tarda en recorrerse
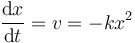
Esto quiere decir que el tiempo necesario para recorrer dx es, despejando,
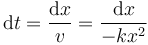
Sumando (es decir, integrando) todos los diferenciales obtenemos el tiempo necesario para llegar a una cierta posición
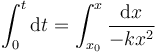
lo que da
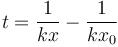
Despejamos de aquí x y da