Análisis numérico de movimiento (GIOI)
De Laplace
Contenido |
1 Enunciado
La posición de una partícula en distintos instantes de tiempo es, aproximadamente
| t (s) | 0.0 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
|---|---|---|---|---|---|---|---|
| x (m) | −1.728 | −0.440 | 0.560 | 1.296 | 1.792 | 2.072 | 2.160 |
| t (s) | 0.7 | 0.8 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 |
|---|---|---|---|---|---|---|---|
| x (m) | 2.080 | 1.856 | 1.512 | 1.072 | 0.560 | 0.000 | −0.584 |
| t (s) | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 2.0 |
|---|---|---|---|---|---|---|---|
| x (m) | −1.168 | −1.728 | −2.240 | −2.680 | −3.024 | −3.248 | −3.328 |
Para este movimiento, halle:
- El desplazamiento entre
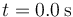 y
y 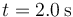 , así como el valor aproximado de la distancia recorrida en dicho intervalo.
, así como el valor aproximado de la distancia recorrida en dicho intervalo.
- La velocidad media y la rapidez media en el intervalo anterior.
- La velocidad media en los intervalos (0.0s, 0.6s), (0.2s, 1.1s) y (0.6s, 1.5s).
- El valor aproximado de la velocidad en
 .
.
- El valor aproximado de la aceleración en
 .
.
- Sabiendo que este movimiento sigue una ley de la forma
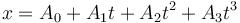
- Calcule
- Los valores de las constantes Ak.
- El valor exacto de la distancia recorrida y la rapidez media.
- El valor exacto de la velocidad y de la aceleración en
 .
.
2 Desplazamiento en el intervalo completo
2.1 Desplazamiento
El desplazamiento lo calculamos como la diferencia entre la posición final y la inicial
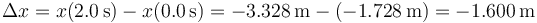
Este desplazamiento corresponde gráficamente a la distancia vertical entre el punto inicial y el final.

2.2 Distancia recorrida
Podemos hallar de forma aproximada la distancia recorrida sumando las diferencias entre posiciones, con valor absoluto.
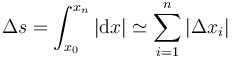
Para ello, construimos una tabla de diferencias y sumamos (con ayuda de un ordenador).
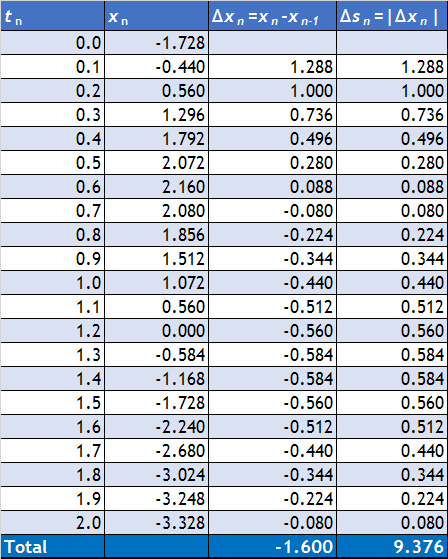
Vemos que la distancia recorrida es de 9.376m.
Este procedimiento es general siempre que tengamos una tabla de valores. Sin embargo, para este caso podemos calcular la distancia recorrida por simple inspección. Vemos que la masa parte de un valor de x negativo va aumentando hasta un máximo y a partir de ahi retrocede hasta otro valor negativo. Podemos hallar la distancia total sumando lo que recorre en la ida con lo que recorre en la vuelta
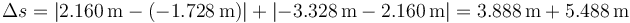
3 Velocidad y rapidez media
La velocidad media la calculamos como el desplazamiento dividido por el intervalo de tiempo
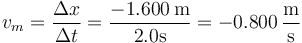
y la rapidez media se calcula de la misma forma pero con la distancia recorrida
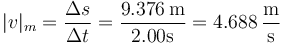
4 Velocidades medias
Para cada uno de los tres intervalos se calcula la velocidad media como el cociente entre el desplzamiento y el intervalo. Resulta en el primer caso
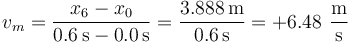
en el segundo
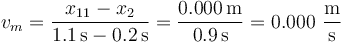
y en el tercero
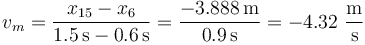
Vemos que la velocidad media puede tener cualquier signo o ser nula, dependiendo de hacia donde es el desplazamiento. En cada caso se trata de la pendiente de la secante que pasa por los dos instantes indicados.

5 Velocidad instantánea
Para calcular la velocidad instantánea necesitamos hallar la derivada, lo cual no podemos hacer exactamente pues no disponemos de una función para derivar.
No obstante, si el intervalo de tiempo es pequeño, podemos aproximar la velocidad instantánea por la velocidad media en ese pequeño intervalo.
En este caso podemos tomar el intervalo (1.1s,1.2s) y el (1.2s,1.3s). En el primer caso obtenemos la aproximación
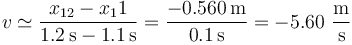
y en el segundo
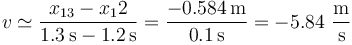
Una mejor aproximación es la media de estos dos valores
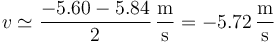
Con ayuda del ordenador podemos calcular la velocidad instantánea aproximada para cada par de datos, añadiendo una nueva columna a la tabla.
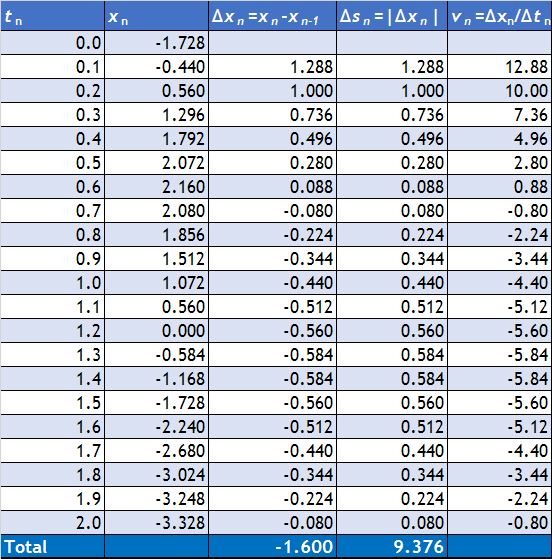
6 Aceleración instantánea
Para el cálculo aproximado de la aceleración instantánea realizamos el mismo razonamiento empleando el incremento de velocidades
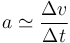
En nuestro caso, ya hemos calculado la velocidad un poco antes y un poco después del instante t =1.2s, por lo que podemos emplearlas para estimar la aceleración
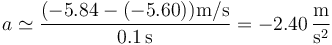
De nuevo podemos construir una tabla de las aceleraciones aproximadas en cada instante
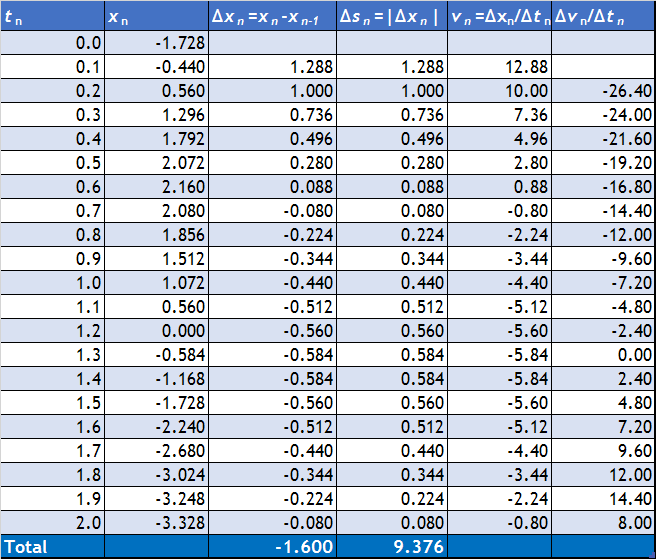
Vemos que en cada derivación aproximada vamos perdiendo una fila de datos, ya que cada uno se calcula a partir de diferencias entre valores sucesivos.
Nótese también que una cosa es la posición, una diferente la velocidad y otra distinta la aceleración. En los puntos en que la posición es nula la velocidad no lo es y viceversa, y lo mismo ocurre con la velocidad y la aceleración.
7 Cálculos exactos
Cuando de lo que se dispone es de una serie de datos numéricos pueden hacerse cálculos analíticos buscando funciones que se aproximen a la serie de datos. Existen diferrentes técnicas aunque es habitual aproximar la función que pasa por varios puntos sucesivos como una parábola o una cúbica.
En este caso se nos dice explícitamente que existe una función cúbica que pasa por todos los puntos.
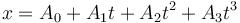
Para determinar estos coeficientes nos basta con imponer por cuatro de los puntos. Lo más sencillo es elegir los valores enteros del tiemo (0.0s, 1.0s y 2.0s) y, dado que necesitamos cuatro, como cuarto punto tomamos 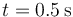 . Si sustituimos nos queda el sistema de ecuaciones
. Si sustituimos nos queda el sistema de ecuaciones
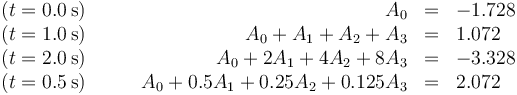
con solución, en el SI,

de manera que la fórmula analítica es
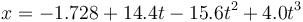
A partir de aquí podemos calcular la distancia recorrida. Hallamos en primer lugar la velocidad
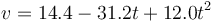
Si resolvemos la ecuación de segundo grado v = 0 vemos que se anula en 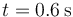 y en
y en 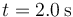 (como se ve de la propia gráfica, donde es máxima y mínima la posición). Hasta 0.6s es positiva y de ahí en adelante negativa, por lo que la distancia recorrida vale
(como se ve de la propia gráfica, donde es máxima y mínima la posición). Hasta 0.6s es positiva y de ahí en adelante negativa, por lo que la distancia recorrida vale
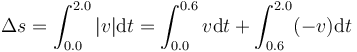
Las integrales son de una simple función polinómica de integral inmediata. El resultado es
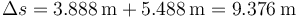
El resultado coincide con el que hallamos a partir de la serie de datos por coincidir el máximo con uno de los puntos de la serie.
La rapidez media, lógicamente, es la misma que ya conocemos
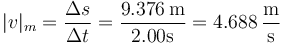
Para la velocidad instantánea sustituimos t por 1.2s y queda
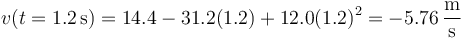
Si comparamos este valor con el de −5.72m/s que hallamos antes, vemos que la diferencia es del 0.7%.
Para hallar la aceleración derivamos de nuevo
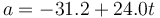
que en  vale
vale
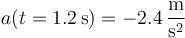
que en este caso coincide con el valor obtenido a partir de la serie de datos.





