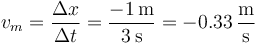Entrar Página Discusión Historial Go to the site toolbox

Posición dependiente del tiempo (GIOI)

De Laplace

Contenido

1 Enunciado

Una partícula se mueve de manera que su posición como función del tiempo está representada en la gráfica de la figura

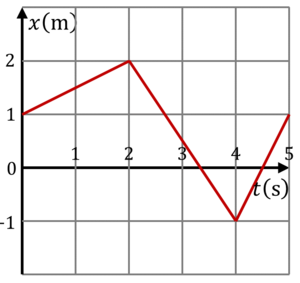
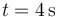  1. ¿Cuánto vale su desplazamiento entre t=0\,\mathrm{s} y t=4\,\mathrm{s} ?
  2. ¿Cuánto vale la distancia total recorrida en el mismo intervalo?
  3. ¿Cuánto vale el desplazamiento y la distancia total recorrida en el intervalo (0 s,5 s)?
  4. ¿Cuánto vale la velocidad media en los intervalos (0 s,5 s), (0 s,4 s) y (2 s,5 s)?
  5. ¿Cómo es la gráfica de la velocidad instantánea como función del tiempo?

2 Desplazamiento

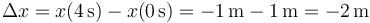
\Delta x = x(4\,\mathrm{s})-x(0\,\mathrm{s})=-1\,\mathrm{m}-1\,\mathrm{m}=-2\,\mathrm{m}

3 Distancia recorrida

Es la suma de la que avanza hasta t=2\,\mathrm{s} y la que retrocede desde ese momento

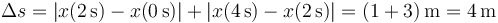
\Delta s = |x(2\,\mathrm{s})-x(0\,\mathrm{s})|+|x(4\,\mathrm{s})-x(2\,\mathrm{s})|=(1+3)\,\mathrm{m}=4\,\mathrm{m}

4 Desplazamiento y distancia

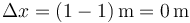
\Delta x = (1-1)\,\mathrm{m}=0\,\mathrm{m}
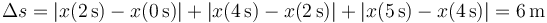
\Delta s = |x(2\,\mathrm{s})-x(0\,\mathrm{s})|+|x(4\,\mathrm{s})-x(2\,\mathrm{s})|+|x(5\,\mathrm{s})-x(4\,\mathrm{s})|=6\,\mathrm{m}

5 Velocidades medias

5.1 Entre 0s y 5s

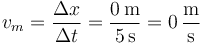
v_m=\frac{\Delta x}{\Delta t}=\frac{0\,\mathrm{m}}{5\,\mathrm{s}}=0\,\frac{\mathrm{m}}{\mathrm{s}}

5.2 Entre 0 y 4s

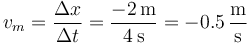
v_m=\frac{\Delta x}{\Delta t}=\frac{-2\,\mathrm{m}}{4\,\mathrm{s}}=-0.5\,\frac{\mathrm{m}}{\mathrm{s}}

5.3 Entre 2 y 5 s

v_m=\frac{\Delta x}{\Delta t}=\frac{-1\,\mathrm{m}}{3\,\mathrm{s}}=-0.33\,\frac{\mathrm{m}}{\mathrm{s}}

6 Gráfica de la velocidad

Obtenido de "http://tesla.us.es/wiki/index.php/Posici%C3%B3n_dependiente_del_tiempo_(GIOI)"

Herramientas:

TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 13:25, 24 sep 2019. - Esta página ha sido visitada 608 veces. - Aviso legal - Acerca de Laplace