Problemas de potencial eléctrico (GIA)

De Laplace

Revisión de 11:57 13 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Potencial en sistema de conductores planos con medio inhomogéneo) ← Edición más antigua		Revisión de 11:58 13 jul 2018 (ver código fuente) Gabriel (Discusión | contribuciones) (→Potencial en sistema de conductores planos con medio inhomogéneo) Edición más nueva →
Línea 78:		Línea 78:
	==[[Potencial en sistema de conductores planos con medio inhomogéneo (GIA)|Potencial en sistema de conductores planos con medio inhomogéneo]]==		==[[Potencial en sistema de conductores planos con medio inhomogéneo (GIA)|Potencial en sistema de conductores planos con medio inhomogéneo]]==
-	[[Archivo:f2_gIA_ex1ac_17_18_e3_0.png|right]]Dos cuerpos conductores,<math>\mathrm{C}_1</math> y <math>\mathrm{C}_2</math>, presentan sendas superficies planas, perpendiculares al eje <math>OX</math>, que coinciden con los planos geométricos <math>\Pi_1: x=0</math> y con {{qquad}}<math>\Pi_2: x=2a</math>. La distancia de separación, $2a$, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a <math>0<x<a</math> está ocupada por un dieléctrico lineal de constante dieléctrica <math>\kappa</math>, mientras que la comprendida en el intervalo <math>a<x<2a</math> está rellena de aire. El conductor <math>\mathrm{C}_1</math> está conectado a un generador cuya f.e.m. tiene un valor constante <math>V_0</math>, y el <math>\mathrm{C}_2</math> a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya	+	[[Archivo:f2_gIA_ex1ac_17_18_e3_0.png|right]]Dos cuerpos conductores,<math>\mathrm{C}_1</math> y <math>\mathrm{C}_2</math>, presentan sendas superficies planas, perpendiculares al eje <math>OX</math>, que coinciden con los planos geométricos <math>\Pi_1: x=0</math> y con <math>\Pi_2: x=2a</math>. La distancia de separación, $2a$, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a <math>0<x<a</math> está ocupada por un dieléctrico lineal de constante dieléctrica <math>\kappa</math>, mientras que la comprendida en el intervalo <math>a<x<2a</math> está rellena de aire. El conductor <math>\mathrm{C}_1</math> está conectado a un generador cuya f.e.m. tiene un valor constante <math>V_0</math>, y el <math>\mathrm{C}_2</math> a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya
	expresión es:		expresión es:

---

Revisión de 11:58 13 jul 2018

Contenido 1 Energía de los electrones en tubo de imagen 2 Potencial y campo eléctrico de aro cargado uniformemente 3 Potencial en gota de agua cargada eléctricamente 4 Esfera conductora hueca con carga puntual 5 Sistema electrostático de cuatro cargas 6 Trabajo realizado para reunir cuatro cargas puntuales 7 Energía electrostática en sistema de conductores esféricos 8 Placas paralelas a potenciales fijos 9 Potencial en sistema de conductores planos con medio inhomogéneo

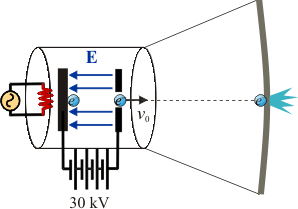
1 Energía de los electrones en tubo de imagen

En el tubo de imagen de un televisor los electrones parten del reposo y se aceleran dentro de una región en la que existe una diferencia de potencial de 30000 V, antes de golpear sobre el revestimiento de material de fósforo de la pantalla. Calcule la velocidad con la que los electrones chocan con la pantalla. Datos: ; .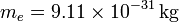

 

 

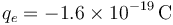2 Potencial y campo eléctrico de aro cargado uniformemente

Tenemos un aro circular de grosor nulo y radio R, con una carga total Q > 0 distribuida uniformemente en su longitud.

1. Calcula el potencial eléctrico en los puntos del eje del anillo.
2. Calcula el campo eléctrico en los puntos del eje del anillo.
3. Se coloca una carga puntual − q (con q > 0) en un punto del eje a una distancia d del centro del aro con velocidad nula. Se deja libre de modo que se mueve a lo largo del eje bajo la acción del campo eléctrico creado por el aro. Describe el movimiento que hace la carga y calcula su velocidad cuando está en el centro del aro.

3 Potencial en gota de agua cargada eléctricamente

Una gota esférica de agua transporta una carga de 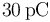uniformemente distribuida en su volumen, siendo el potencial en su superficie de 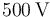(considerando V = 0 en el infinito).

1. ¿Cuál es el radio de la gota?
2. ¿Cuál es el valor del potencial en el centro de la gota?
3. Si esta gota se combina con otra con el mismo radio y la misma carga para formar una sola gota, determine el potencial en la superficie de la nueva gota.

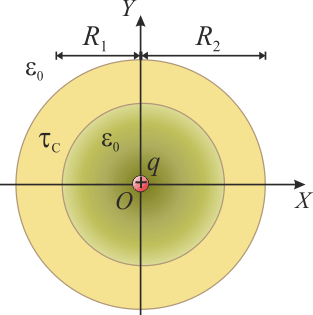
4 Esfera conductora hueca con carga puntual

Una esfera conductora hueca de radios interior R₁ y exterior R₂ tiene en su centro una pequeña partícula cargada con carga q. Suponiendo que la esfera no tiene carga neta y que está aislada calcule el potencial al que se encuentra y la carga que hay en sus superficies interior y exterior.

 

 

 

 

 

 

5 Sistema electrostático de cuatro cargas

Un sistema electrostático está formado por cuatro cargas, que pueden considerarse puntuales. Dos de ellas son positivas, de valor + q, y las otras dos, negativas de valor − q. Estos pares de cargas se hallan en sendas rectas perpendiculares que se cortan en el punto O, y que dentificaremos como los ejes OX y OY, respectivamente. Las cargas positivas se encuentran ambas a una distancia 4a del punto O, mientras que cada una de las negativas se encuentra a una distancia 3a de dicho punto.

1. Obtenga el valor del campo eléctrico y del potencial electrostático en el centro O del sistema.
2. ¿Cómo es la fuerza electrostática que actúa sobre cada una de las cargas, debido a la acción de las otras tres?
3. Si las cantidades de carga en valor absoluto son 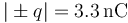, y las distancias están determinadas por el valor 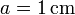, ¿qué trabajo “externo” ha sido necesario realizar, aproximadamente, para reunir las cuatro cargas?
4. Si se coloca un dipolo puntual en el centro O de la distribución, con su momento dipolar 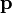orientado en la dirección del eje OY y con el sentido del vector unitario 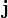, ¿qué acción ejerce sobre él el sistema de cargas descrito?

6 Trabajo realizado para reunir cuatro cargas puntuales

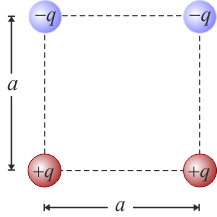
Un sistema electrostático está formado por dos cargas puntuales de valor + q y otras dos − q, situadas en los vértices de un cuadrado de lado a. Las cargas están dispuestas de manera que en los extremos de cada diagonal del cuadrado hay cargas de distinto signo, tal como se muestra en la figura. Calcular el trabajo externo que ha sido necesario realizar para configurar dicho sistema trayendo las cargas desde el infinito.

 

 

 

7 Energía electrostática en sistema de conductores esféricos

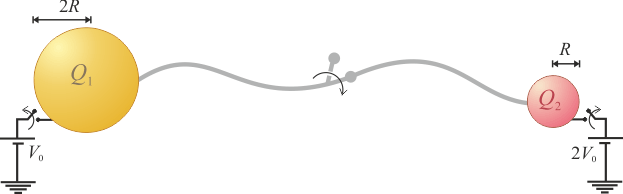
Se tienen dos esferas conductoras separadas por una distancia mucho mayor que sus respectivos radios, R y 2R, de modo que no hay una influencia apreciable entre ellas.

1. Las esferas conductoras se conectan a sendos generadores que establecen valores fijos de potencial, 2V₀ y V₀, respectivamente. Una vez que se han cargado, se procede a su desconexión. ¿Qué cantidad de energía electrostática se almacena en el sistema?
2. Estando en la situación final del apartado anterior, la esferas se conectan entre sí mediante un cable conductor muy largo y con resistencia eléctrica no nula. Determine la cantidad de carga eléctrica y el valor del potencial en cada una de las esferas cuando el sistema recobra el equilibrio. ¿Qué cantidad de energía electrostática se habrá disipado en el cable al final del proceso?

8 Placas paralelas a potenciales fijos

Se tienen cuatro placas conductoras iguales de superficie S dispuestas paralelamente como se indica en la figura. La distancia entre placas vecinas es la misma para todas ellas e igual a d. Las dos placas de los extremos están conectadas a tierra (potencial 0) mientras que las otras dos placas se conectan a los potenciales V₂ = V₀ y V₃ = 2V₀.

1. Calcula los campos eléctricos en las regiones entre placas, indicadas en la figura como a, b y c.
2. Calcula la carga total acumulada en las cuatro placas.
3. Se conectan las placas 2 y 3 con un hilo conductor. Calcula los nuevos valores de los campos y la carga de cada placa.

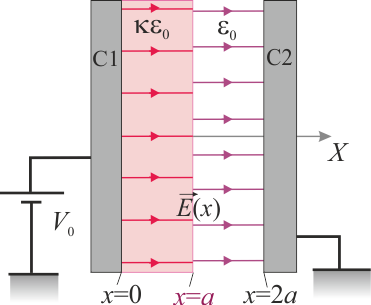
9 Potencial en sistema de conductores planos con medio inhomogéneo

Dos cuerpos conductores,C₁ y C₂, presentan sendas superficies planas, perpendiculares al eje OX, que coinciden con los planos geométricos Π₁:x = 0 y con Π₂:x = 2a. La distancia de separación, $2a$, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a 0 < x < a está ocupada por un dieléctrico lineal de constante dieléctrica κ, mientras que la comprendida en el intervalo a < x < 2a está rellena de aire. El conductor C₁ está conectado a un generador cuya f.e.m. tiene un valor constante V₀, y el C₂ a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya

expresión es:

1. ¿Cómo son las superficies equipotenciales entre los dos conductores? Indique de qué forma varía el valor del potencial de dichas superficies.
2. ¿Qué relación existe entre los valores V₀ y E₀? Obtenga la función V(x) que describe cómo es el valor del potencial en la región 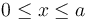(dieléctrico lineal), y en 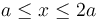(aire).