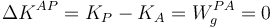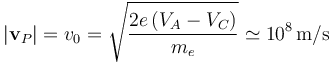Energía de los electrones en tubo de imagen GIA

De Laplace

1 Enunciado

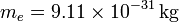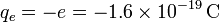En el tubo de imagen de un televisor los electrones parten del reposo y se aceleran dentro de una región en la que existe una diferencia de potencial de 30000 V, antes de golpear sobre el revestimiento de material de fósforo de la pantalla. Calcule la velocidad con la que los electrones chocan con la pantalla. Datos: $m_e=9.11 \times 10^{-31}\,\mathrm{kg}\,$ ; $q_e=-e=-1.6 \times 10^{-19}\,\mathrm{C}\,$ .

2 Solución

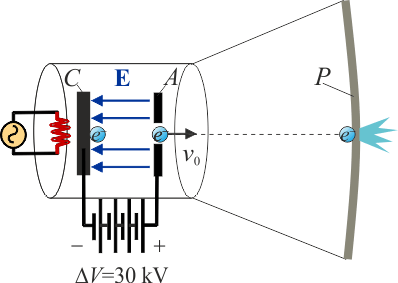
Para producir la emisión de electrones en el tubo de imagen de un antiguo televisores se cuenta con dos electrodos (conductores), llamados ánodo (A) y cátodo (C), entre los que se establece una diferencia de potencial de 30 kV y, por consiguiente, un intenso campo eléctrico, ya que se debe cumplir

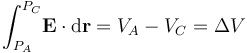
$\int_{P_A}^{P_C}\!\mathbf{E}\cdot\mathrm{d}\mathbf{r}=V_A-V_C=\Delta V$

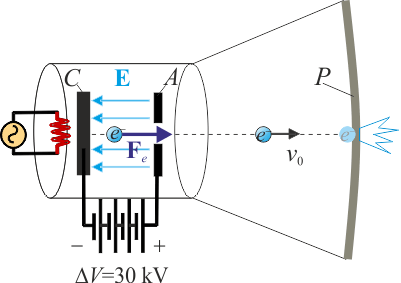
donde $P A$ y $P C$ son, respectivamente, dos puntos cualesquiera de las superficies del ánodo A y del cátodo C (nótese que al ser éstos conductores, sus superficies son equipotenciales donde el potencial tendrá sendos valores $V A$ y $V C$ ). Un filamento incandescente (debido al paso de una corriente eléctrica) calienta el cátodo que, por efecto termoiónico, emite electrones. Puede considerarse que cuando éstos se desprenden del cátodo se hallan prácticamente en reposo, pero la fuerza que ejerce el campo eléctrico sobre ellos, los acelera hacia el ánodo. Este electrodo presenta un orificio por el cuál algunos electrones abandonan la región donde existe la diferencia de potencial. Tras recorrer el interior vacío del tubo de imagen, impactan en el revestimiento de fósforo del interior de la pantalla (P), produciendo un destello.

Por definición, la diferencia de potencial entre los electrodos C y A es el trabajo que por unidad de carga realiza la fuerza eléctrica sobre una carga puntual $Δ q$ cuando ésta se desplaza desde el cátodoo hasta el ánodo. Como, indudablemente, los electrones son cargas puntuales, podemos concluir que el trabajo realizado por el campo eléctrico en el desplazamiento de cada electrón entre los electrodos es,

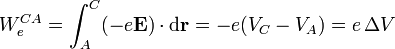
$W_e^{CA}=\int_{A}^C(-e\mathbf{E})\cdot\mathrm{d}\mathbf{r}=-e(V_C-V_A)=e\!\ \Delta V$

Si aplicamos ahora el teorema de la energía cinética al proceso de desplazamiento de cada electrón tendremos que la variación de energía cinética que sufre debe ser igual al trabajo realizado por todas las fuerzas que actúan sobre él. Una de ellas es la fuerza del campo eléctrico, para la que ya hemos calculado el trabajo y que, para los datos del problema, tendría un valor de 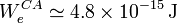$W_e^{CA}\simeq 4.8\times 10^{-15}\,\mathrm{J}$ . Pero puesto que el electrón tiene masa, está sometido al campo gravitatorio terrestre y podríamos pensar, por tanto, que éste también realizará un trabajo 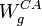$W_g^{CA}$ a lo largo del desplazamiento de electrón entre el ánodo y el cátodo:

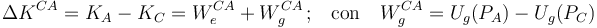
$\Delta K^{CA}=K_A-K_C=W_e^{CA}+W_g^{CA}\!\ \mathrm{;}\quad\mathrm{con}\quad W_g^{CA}=U_g(P_A)-U_g(P_C)$

Obsérvese que dicho trabajo sería igual a una disminución de la energía potencial gravitatoria del electrón al verse arrastrado por la fuerza peso en la dirección de la vertical gravitatoria. Sin embargo, la reducida masa del electrón da lugar a que su variación de energía potencial gravitatoria por unidad de longitud sea

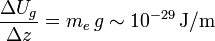
$\frac{\Delta U_g}{\Delta z}=m_e\!\ g \sim 10^{-29}\, \mathrm{J/m}$

Es decir, el electrón debería desplazarse del orden de $1014$ m (¡¡100.000 millones de km!!) en la dirección vertical para que el trabajo de la fuerza gravitatoria fuese comparable al realizado sobre él por el campo eléctrico entre el cátodo y el ánodo. Por tanto, en el sistema bajo estudio podemos despreciar, sin ningún género de dudas, la acción de la gravedad sobre los electrones que se mueven en el tubo de imagen. Por otra parte, como en todo el tubo de imagen se ha hecho el vacío, no hay lugar para fuerzas de fricción o rozamiento. Así, el incremento de energía cinética que sufre cada una de estas partículas entre el cátodo y el ánodo será igual al trabajo realizado por el campo eléctrico. Y puesto que consideramos que el electrón en el cátodo está en reposo, se tendrá:

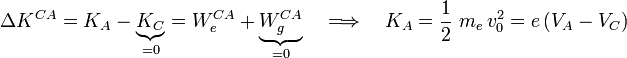
$\Delta K^{CA}=K_A-\underbrace{K_C}_{=0}=W_e^{CA}+\underbrace{W_g^{CA}}_{= 0}\quad\Longrightarrow\quad K_A=\frac{1}{2}\ m_e\!\ v_0^2=e\!\ (V_A-V_C)$

donde $v 0$ es el módulo de la velocidad de los electrones cuando llegan al ánodo, y que será la velocidad inicial que tienen los que logran pasa al tubo de imagen. Obsérvese que entre el ánodo A y la pantalla P no hay campo eléctrico, luego la única fuerza que podría actuar sería el peso del electrón, que ya hemos comprobado que nunca podría llegar a producir cambios significativos en la energía cinética de cada uno de los electrones. Por tanto, si aplicamos de nuevo el teorema de la energía cinética...