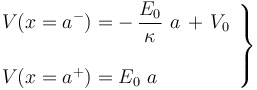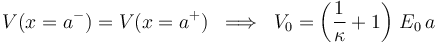Potencial en sistema de conductores planos con medio inhomogéneo (GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Potencial electrostático y superficies equipotenciales
- 2.2 Expresión del potencial electrostático

1 Enunciado

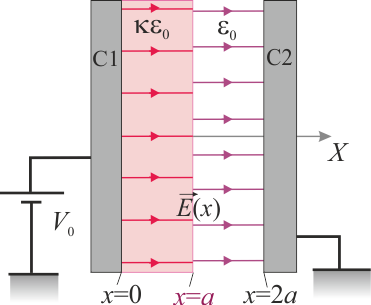
Dos cuerpos conductores,

C 1

y

C 2

, presentan sendas superficies planas, perpendiculares al eje

O X

, que coinciden con los planos geométricos

Π 1 : x = 0

y con

Π 2 : x = 2 a

. La distancia de separación,

2 a

, es significativamente menor que las dimensiones de los planos conductores. La región correspondiente a

0 < x < a

está ocupada por un dieléctrico lineal de constante dieléctrica

κ

, mientras que la comprendida en el intervalo

a < x < 2 a

está rellena de aire. El conductor

C 1

está conectado a un generador cuya f.e.m. tiene un valor constante

V 0

, y el

C 2

a tierra. Esta diferencia de potencial entre los conductores determina la presencia de un campo eléctrico en la región dieléctrica que los separa, y cuya expresión es:

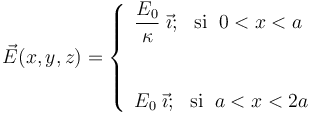
$\vec{E}(x,y,z)=\left\{ \begin{array} {l} \displaystyle \frac{E_0}{\kappa}\; \vec{\imath}\mathrm{;}\;\;\;\mathrm{si}\;\; 0<x<a \\ \\ \\ \displaystyle E_0\; \vec{\imath}\mathrm{;}\;\;\;\mathrm{si}\;\; a<x<2a \end{array}\right.$

¿Cómo son las superficies equipotenciales entre los dos conductores? Indique de qué forma varía el valor del potencial de dichas superficies.
¿Qué relación existe entre los valores $V 0$ y $E 0$ ? Obtenga la función $V (x)$ que describe cómo es el valor del potencial en la región 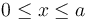$0\leq x\leq a$ (dieléctrico lineal), y en 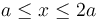$a\leq x\leq 2a$ (aire).

2 Solución

Planteamiento

Toda distribución de cargas eléctricas estáticas produce una perturbación eléctrica en el espacio que puede ser descrita mediante sendos campos: el campo eléctrico 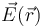$\displaystyle \vec{E}(\vec{r})$ , de naturaleza vectorial; o el campo escalar potencial electrostático 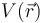$\displaystyle V(\vec{r})$ . La primera de estas magnitudes físicas se define como la fuerza eléctrica que por unidad de carga experimentaría una carga puntual situada en el punto P del espacio, determinado por el radiovector $\vec{r}$ . Y puesto que dicho fuerza es conservativa, es posible definir la energía potencial electrostática de una carga puntual cuando se encuentra sometida a la acción de las cargas que crean la perturbación eléctrica analizada. 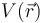El potencial eléctrostatico $\displaystyle V(\vec{r})$ es la energía potencial que por unidad de carga tendría una carga puntual situada en el punto P, dado por el radio vector $\vec{r}$ .

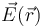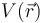Ambas magnitudes físicas son dos formas de expresar los efectos producidos por una determinada distribución de carga, que se relacionan a partir de la definición de diferencia de potencial: los campos $\displaystyle \vec{E}(\vec{r})$ e $\displaystyle V(\vec{r})$ creado por una determinada distribución de carga eléctrica en un región del espacio son tales que la diferencia entre los valores del potencial entre dos puntos A y B de dicha región es igual a la circulación (o integral de camino) del campo eléctrico entre dichos puntos:

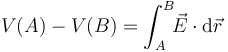
$V(A) - V(B)=\int_A^B\!\! \vec{E}\cdot\mathrm{d}\vec{r}$

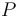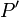Y puesto que el campo eléctrico es una magnitud física, su módulo ha de ser una cantidad finita expresable mediante un número real. Por tanto, si consideramos dos puntos, $\displaystyle P$ y $P^\prime$ , separados una distancia infinitesimal, entonces se cumplirá,

$V(P^\prime)=V(P)+\mathrm{d}V\mathrm{,}\;\;\,\mathrm{tal}\,\;\,\mathrm{que}\,\;\;\;\mathrm{d}V=-\ \vec{E}(P)\cdot\mathrm{d}\vec{r}\,\mathrm{,}\,$

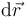siendo $\displaystyle \mathrm{d}\vec{r}$ el vector de módulo infinitesimal que determina la posición de 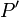$P^\prime$ , respecto de 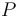$\displaystyle P$ . Este resultado permite identificar al vector campo eléctrico como el vector opuesto al gradiente del potencial eléctrostático en dicho punto.En terminos del operador nabla, se tendrá:

$\vec{E}(\vec{r})=-\overrightarrow{\mathrm{grad}}\!\ \big[V(\vec{r})\big]=-\vec{\nabla}V(\vec{r})$

Por tanto, el campo eléctrico en un punto es un vector que indica la dirección y el sentido en que se verifica la máxima disminución del valor del potencial, y cuyo módulo es la variación por unidad de longitud del potencial en el entorno de dicho punto. Por otra parte, si desde el punto 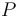$\displaystyle P$ nos desplazamos a puntos infinitamente próximos situados en la misma superficie equipotencial, la variación del potencial va a ser nula; por tanto, en general se tendrá que el campo eléctrico en $P$ va a ser perpendicular al plano tangente a la superficie equipotencial en dicho punto.

Para la resolución del ejercicio propuesto resulta especialmente interesante esta interpretación de campo eléctrico y potencial. Si se utilizan las coordenadas cartesianas para la descripción analítica del espacio, con el punto $O$ como origen del sistema de referencia $O X Y Z$ , y de manera que para un punto $P$ del espacio, se tendrá que:

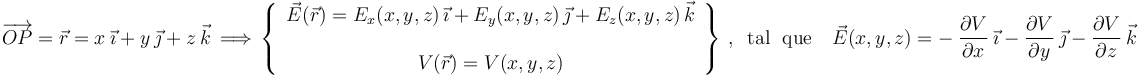
$\overrightarrow{OP}=\vec{r}=x\ \vec{\imath}\ +\ y\ \vec{\jmath}\ +\ z\ \vec{k}\,\Longrightarrow\,\left\{\begin{array}{c}\vec{E}(\vec{r})=E_x(x,y,z)\!\ \vec{\imath} + E_y(x,y,z)\!\ \vec{\jmath}+ E_z(x,y,z)\!\ \vec{k}\\ \\ V(\vec{r})=V(x,y,z)\end{array}\right\}\,\mathrm{,}\;\;\,\mathrm{tal}\,\;\,\mathrm{que}\,\;\;\;\vec{E}(x,y,z)=-\ \frac{\partial V}{\partial x}\ \vec{\imath}\ -\ \frac{\partial V}{\partial y}\ \vec{\jmath}\ -\ \frac{\partial V}{\partial z}\ \vec{k}$

2.1 Potencial electrostático y superficies equipotenciales

Como sabemos, las superficies conductoras en condiciones electrostáticas, son superficies equipotenciales. Es decir, al estar el conductor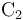 $\,\mathrm{C}_2\,$ conectado a tierra, el potencial en todos los puntos de la superficie 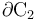$\,\partial\mathrm{C}_2\,$ tendrá el valor de referencia, que tomaremos como valor nulo. Por su parte, si el conductor 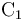$\,\mathrm{C}_1\,$ está conectado al electrodo activo de un generador electrostático de f.e.m.

V 0

, respecto del valor de referencia, todos los puntos de la superficie 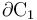$\,\partial\mathrm{C}_1\,$ estarán a aquél valor de potencial. En particulas las superficies planas

Π 1

y

Π 2

de dichos conductores serán superficies equipotenciales con valores de potencial

V 0

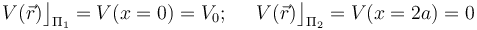
y 0, respectivamente: $V(\vec{r})\big\rfloor_{\Pi_1}=V(x=0)=V_0\mathrm{;}\,\;\;\;\;\;V(\vec{r})\big\rfloor_{\Pi_2}=V(x=2a)=0$

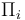Por otra parte, en el enunciado se informa de que en cualquier punto P situado entre ambos planos, el campo eléctrico tiene la dirección paralela al eje $O X$ . Por tanto, las superficies equipotenciales van a ser los planos perpendiculares al vector unitario cartesiano $\vec{\imath}$ , que son planos formados por puntos que tienen igual componente “ $x$ ”. La comprobación es sencilla: sea $\displaystyle\Pi_i$ el plano formado por todos aquellos puntos con igual valor 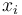$\displaystyle x_i$ en la coordenada “ $x$ ”. El vector desplazamiento entre dos puntos infinitamente próximos de dicho plano no va a tener componente en la dirección del eje $O X$ ; por tanto, dicho vector será perpendicular al campo eléctrico en cualquiera de ellos, y no habrá variación del potencial entre ambos. 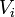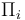En consecuencia, el potencial tendrá el mismo valor $\displaystyle V_i$ en todos los puntos del plano $\displaystyle \Pi_i$ :

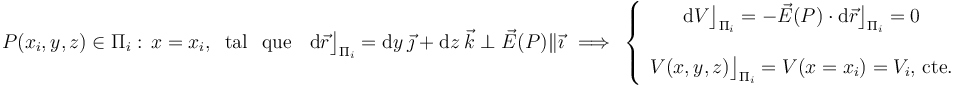
$P(x_i,y,z)\in\Pi_i:\,x=x_i\mathrm{,}\,\;\;\mathrm{tal}\,\;\;\mathrm{que}\,\;\;\,\mathrm{d}\vec{r}\big\rfloor_{\Pi_i}=\mathrm{d}y\ \vec{\jmath}\ + \ \mathrm{d}z\ \vec{k}\perp\vec{E}(P)\|\vec{\imath}\,\;\Longrightarrow\,\;\left\{\begin{array}{c}\mathrm{d}V\big\rfloor_{\Pi_i}=-\vec{E}(P)\cdot\mathrm{d}\vec{r}\big\rfloor_{\Pi_i}=0\\ \\ V(x,y,z)\big\rfloor_{\Pi_i}=V(x=x_i)=V_i\mathrm{,}\,\,\mathrm{cte.}\end{array}\right.$

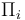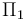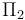Es decir, las superficies equipotenciales en el sistema electrostático bajo estudio son cada uno de los planos $\displaystyle\Pi_i$ paralelos a las superficies conductoras $\displaystyle\Pi_1$ y $\displaystyle\Pi_2$ , al menos en el espacio comprendido entre dichos planos, y tanto en la región rellena de dieléctrico lineal ( 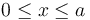$\displaystyle 0\leq x\leq a$ ), como en la de aire ( 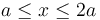$\displaystyle a\leq x\leq 2a$ ), como en la . Además, los valores del potencial en cada uno de estos planos disminuyen en la dirección y el sentido indicado por el campo eléctrico, desde el valor 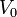$\displaystyle V_0$ , hasta el valor 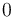$\displaystyle 0$ . Asumiendo que 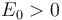$\displaystyle E_0>0$ , se tendrá:

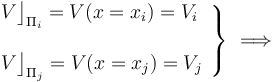
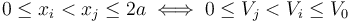
$\left.\begin{array}{l}\displaystyle V\big\rfloor_{\Pi_i}=V(x=x_i)=V_i\\ \\ \displaystyle V\big\rfloor_{\Pi_j}=V(x=x_j)=V_j\end{array}\right\}\ \Longrightarrow$ $0\leq x_i < x_j\leq 2a \;\Longleftrightarrow\; 0\leq V_j<V_i\leq V_0$

2.2 Expresión del potencial electrostático

Los resultados discutidos en el apartado anterior en relación con las superficies equipotenciales, pueden ser constrastados con la obtención de la expresión analítica correspondiente a la función del campo para el potencial electrostático, 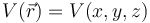$\displaystyle V(\vec{r})=V(x,y,z)$ , en los puntos 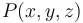$\displaystyle P(x,y,z)$ comprendidos entre los planos $\displaystyle\Pi_1$ y $\displaystyle\Pi_2$ . Utilizando la expresión del campo eléctrico como el vector opuesto al gradiente del potencial, obtenemos el conjunto de ecuaciones diferenciales que permiten determinar la función potencial electrostático:

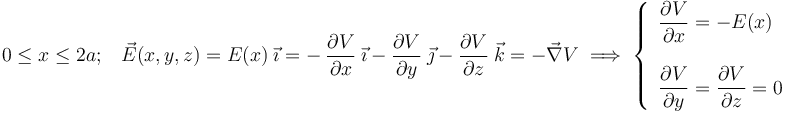
$0\leq x\leq 2a\mathrm{;}\,\;\;\; \vec{E}(x,y,z)=E(x)\ \vec{\imath}=-\ \frac{\partial V}{\partial x}\ \vec{\imath}\ -\ \frac{\partial V}{\partial y}\ \vec{\jmath}\ -\ \frac{\partial V}{\partial z}\ \vec{k}=-\vec{\nabla}V\;\Longrightarrow\;\left\{\begin{array}{l}\displaystyle \frac{\partial V}{\partial x}=-E(x)\\ \\ \displaystyle \frac{\partial V}{\partial y}=\frac{\partial V}{\partial z}=0\end{array}\right.$

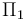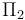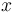En primer lugar, las anteriores ecuaciones diferenciales en derivadas parciales indican que en ambas regiones dieléctricas comprendidas entre las superficies conductoras $\displaystyle\Pi_1$ y $\displaystyle\Pi_2$ , el potencial electrostático es exclusivamente función de la coordenada “ $\displaystyle x$ ”:

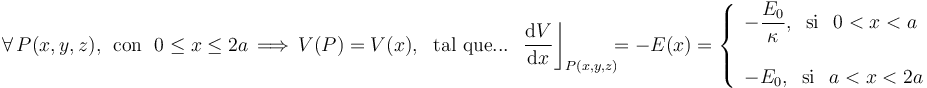
$\forall\,P(x,y,z)\mathrm{,}\,\;\,\mathrm{con}\,\;\,0\leq x\leq 2a\,\Longrightarrow\,V(P)=V(x)\mathrm{,}\,\,\;\,\mathrm{tal}\,\,\mathrm{que...}\,\;\;\frac{\mathrm{d}V}{\mathrm{d}x}\bigg\rfloor_{P(x,y,z)}\!\!\!=-E(x)=\left\{\begin{array}{l}\displaystyle -\frac{E_0}{\kappa}\mathrm{,}\,\;\;\mathrm{si}\,\;\; 0<x<a\\ \\ \displaystyle -E_0\mathrm{,}\,\;\;\mathrm{si}\,\;\; a<x<2a\end{array}\right.$

Obsérvese que, en consecuencia, el valor del potencial será idéntico en todos los puntos que tenga igual valor en la coordenada cartesiana “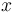 $\displaystyle x$ ”; es decir, las superficies equipotenciales entre los conductores coincidirán con los planos cartesianos 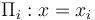$\displaystyle \Pi_i:x=x_i$ , constante. Por otra parte, la relación que deben verificar potencial y campo eléctrico establece que la derivada de la función potencial con respecto a la variable “ 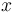$\displaystyle x$ ” presenta valores constantes distintos en las regiones de dieléctrico lineal y de aire. En cualquier caso, el potencial va a presentar un comportamiento lineal con respecto a dicha coordenada cartesiana, pero correspondiéndole funciones distintas en cada uno de esos medios:

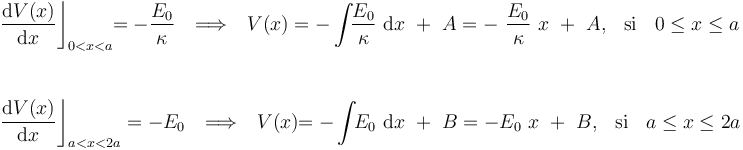
$\begin{array}{l}\displaystyle \frac{\mathrm{d}V(x)}{\mathrm{d}x}\bigg\rfloor_{0<x<a}\!\!=-\frac{E_0}{\kappa}\,\;\;\Longrightarrow\,\;\;V(x)=-\int\!\!\frac{E_0}{\kappa}\ \mathrm{d}x \ +\ A=-\ \frac{E_0}{\kappa}\ x \ +\ A\mathrm{,}\,\;\;\,\mathrm{si}\,\;\;\, 0\leq x\leq a\\ \\ \\ \displaystyle \frac{\mathrm{d}V(x)}{\mathrm{d}x}\bigg\rfloor_{a<x<2a}=-E_0\,\;\;\Longrightarrow\,\;\;V(x)\!\!=-\int\!\!E_0\ \mathrm{d}x \ +\ B=-E_0\ x \ +\ B\mathrm{,}\,\;\;\,\mathrm{si}\,\;\;\, a\leq x\leq 2a\end{array}$

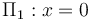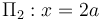donde A y B son constantes a determinar, en función de la geometría y las propiedades eléctricas del sistema. Para ello, se exige que se verifiquen las condiciones de contorno impuestas en los planos conductores $\displaystyle \Pi_1:x=0$ y $\displaystyle \Pi_2:x=2a$ ,

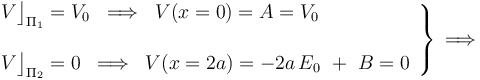
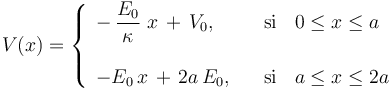
$\left.\begin{array}{l}\displaystyle V\big\rfloor_{\Pi_1}=V_0\;\;\Longrightarrow\;\; V(x=0)=A=V_0\\ \\ \displaystyle V\big\rfloor_{\Pi_2}=0\;\;\Longrightarrow\;\; V(x=2a)=-2a\!\ E_0\ +\ B=0\end{array}\right\}\,\Longrightarrow$ $V(x)= \left\{\begin{array}{ll}\displaystyle -\!\ \frac{E_0}{\kappa}\ x\!\ + \!\ V_0\mathrm{,}&\,\;\;\,\mathrm{si}\,\;\;\, 0\leq x\leq a\\ \\ \displaystyle -E_0\!\ x\!\ + \!\ 2a\!\ E_0\mathrm{,}&\,\;\;\,\mathrm{si}\,\;\;\, a\leq x\leq 2a\end{array}\right.$

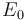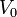
Relación entre los valores $\displaystyle E_0$ y $\displaystyle V_0$

Para obtener dicha relación exijimos que se verifique una condición más: la condición de continuidad para el potencial en la interfaz dieléctrico-vacío localizada en el plano 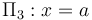$\displaystyle \Pi_3:x=a$ ,

$\left.\begin{array}{l}\displaystyle V(x=a^-)=-\!\ \frac{E_0}{\kappa}\ a\!\ + \!\ V_0\\ \\ V(x=a^+)= E_0\ a\end{array}\right\}$ $V(x=a^-)=V(x=a^+)\;\;\Longrightarrow\;\; V_0=\left(\frac{1}{\kappa}+1\right)\!\ E_0\!\ a$

Potencial en sistema de conductores planos con medio inhomogéneo (GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Potencial electrostático y superficies equipotenciales

2.2 Expresión del potencial electrostático

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES