Placas paralelas a potencial dado Primera Convocatoria Ordinaria 2010/11 (F2GIA)
De Laplace
Contenido |
1 Enunciado
Se tienen cuatro placas conductoras iguales de superficie S dispuestas paralelamente como se indica en la figura. La distancia entre placas vecinas es la misma para todas ellas e igual a d. Las dos placas de los extremos están conectadas a tierra (potencial 0) mientras que las otras dos placas se conectan a los potenciales V2 = V0 y V3 = 2V0.
- Calcula los campos eléctricos en las regiones entre placas, indicadas en la figura como a, b y c.
- Calcula la carga total acumulada en las cuatro placas.
- Se conectan las placas 2 y 3 con un hilo conductor. Calcula los nuevos valores de los campos y la carga de cada placa.
2 Solución
2.1 Campo entre placas
El campo generado por un plano infinito con una densidad uniforme de carga eléctrica es uniforme y perpendicular al plano. Cuando tenemos varios planos infinitos paralelos entre sí el campo en cada espacio entre planos es uniforme y perpendicular a ellos.
En este caso, el dato que nos dan es el potencial al que están los planos, no las densidades de carga en ellos. Por tanto determinamos el campo en cada región en función de la diferencia de potencial entre planos. El campo en cada región es
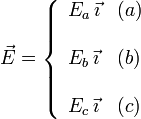
En la región la circulación del campo a lo largo de una línea recta que una las placas 1 y 2 es igual a la diferencia de potencial eléctrico entre ellas. Tenemos
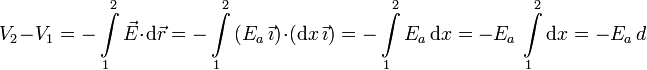
Por tanto, y aplicando un razonamiento similar en las tres regiones entre placas tenemos
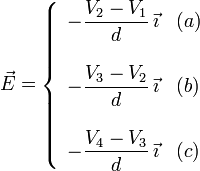
Según los datos del problema

Por tanto el campo en cada región es
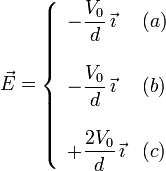
2.2 Carga en las placas
La figura muestra la orientación del campo en cada región suponiendo que V0 es positiva. El campo va desde los potenciales altos hacia los bajos. También va desde las cargas positivas hacia las negativas. En la figura se indica el signo de la carga acumulada en cada una de las caras de las placas.
En cada cara la densidad superficial de carga es

La carga total en cada superficie es
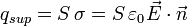
donde 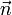 es un vector normal a la superficie de la placa y que sale de ella. Según esto la carga
en cada placa es la suma de la carga en su cara izquierda y la carga en su cara derecha. Tenemos
es un vector normal a la superficie de la placa y que sale de ella. Según esto la carga
en cada placa es la suma de la carga en su cara izquierda y la carga en su cara derecha. Tenemos
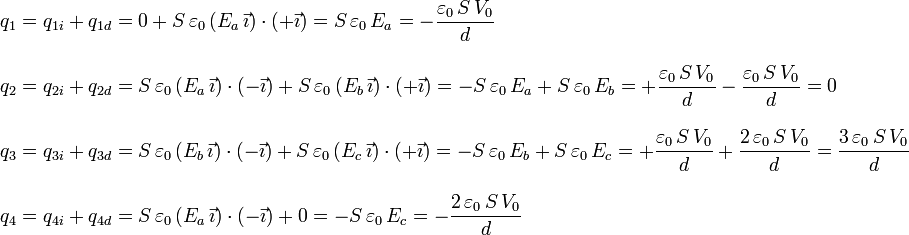
Puede comprobarse que la suma total de todas las carga es cero, como debe ser pues las superficies cargadas están en influencia total dos a dos.
2.3 Conexión de las placas 2 y 3
Al conectar las placas 2 y 3 las cargas presentes en ellas se redistribuyen, y también las cargas en las placas 1 y 2, pues están conectadas a tierra, que no es otra cosa que un conductor externo a potencial fijo.
El campo en la región b es ahora nulo, pues las placas 2 y 3 están al mismo potencial. Los datos que tenemos sobre el potencial y/o las cargas de las placas son

No sabemos cual es el potencial V'2 del conductor 2+3, pero sabemos que tiene un valor fijado. Usando el mismo razonamiento que en el apartado 1, el campo en cada región es
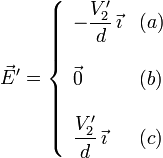
La carga total en el conductor 2+3 es la suma de la carga en la cara izquierda de la placa 2 y la derecha de la placa 3

Sabemos que esta carga debe ser igual a la que había en las placas 2 y 3 antes de la conexión. Es decir
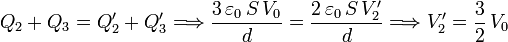
El campo es

y las carga en cada placa
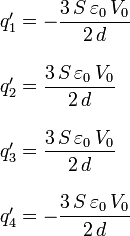
La imagen de la derecha indica el sentido del campo en cada región y el signo de las cargas en cada placa, suponiendo que V0 es positivo.









