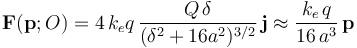Sistema electrostático de cuatro cargas, F2 GIA (Abr, 2013)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un sistema electrostático está formado por cuatro cargas, que pueden considerarse puntuales. Dos de ellas son positivas, de valor

+ q

, y las otras dos, negativas de valor

- q

. Estos pares de cargas se hallan en sendas rectas perpendiculares que se cortan en el punto

O

, y que dentificaremos como los ejes

O X

y

O Y

, respectivamente. Las cargas positivas se encuentran ambas a una distancia

4 a

del punto

O

, mientras que cada una de las negativas se encuentra a una distancia

3 a

de dicho punto.

Obtenga el valor del campo eléctrico y del potencial electrostático en el centro $O$ del sistema.
¿Cómo es la fuerza electrostática que actúa sobre cada una de las cargas, debido a la acción de las otras tres?
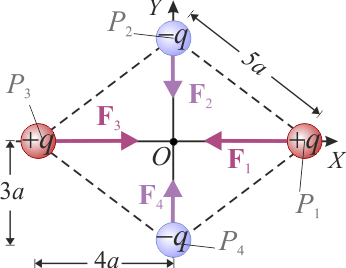
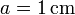Si las cantidades de carga en valor absoluto son $|\pm q|=3.3\,\mathrm{nC}$ , y las distancias están determinadas por el valor $a=1\,\mathrm{cm}$ , ¿qué trabajo “externo” ha sido necesario realizar, aproximadamente, para reunir las cuatro cargas?
Si se coloca un dipolo puntual en el centro $O$ de la distribución, con su momento dipolar 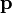$\mathbf{p}$ orientado en la dirección del eje $O Y$ y con el sentido del vector unitario 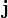$\mathbf{j}$ , ¿qué acción ejerce sobre él el sistema de cargas descrito?

2 Solución

2.1 Campo eléctrico y potencial electrostático en el centro de la distribución

Sean $P 1$ , $P 2$ , $P 3$ y $P 4$ los puntos donde se encuentran las cuatro cargas que constituyen el sistema, de manera que si 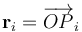$\mathbf{r}_i=\overrightarrow{OP}_i$ es el radio-vector que determina la posición de la carga $q i$ , respecto del centro $O$ del sistema (tomado como origen del sistema de referencia), se tendrá:

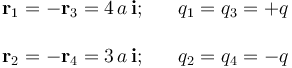
$\begin{array}{ll}\displaystyle\mathbf{r}_1=-\mathbf{r}_3=4\!\ a \!\ \mathbf{i}\mathrm{;}&\quad q_1=q_3=+q\\ \\ \displaystyle\mathbf{r}_2=-\mathbf{r}_4=3\!\ a \!\ \mathbf{i}\mathrm{;}&\quad q_2=q_4=-q\end{array}$

Los campos eléctrico 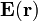$\mathbf{E}(\mathbf{r})$ , y potencial electrostático 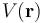$V(\mathbf{r})$ creados por esta distribución de cargas responden a las expresiones

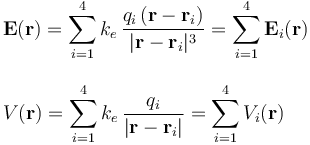
$\begin{array}{l}\displaystyle\mathbf{E}(\mathbf{r})= \sum_{i=1}^4k_e\!\ \frac{q_i\!\ (\mathbf{r}-\mathbf{r}_i)}{|\mathbf{r}-\mathbf{r}_i|^3}=\sum_{i=1}^4 \mathbf{E}_i(\mathbf{r})\\ \\ \displaystyle V(\mathbf{r})= \sum_{i=1}^4k_e\!\ \frac{q_i}{|\mathbf{r}-\mathbf{r}_i|}=\sum_{i=1}^4 V_i(\mathbf{r})\end{array}$

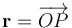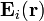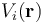donde $\mathbf{r}=\overrightarrow{OP}$ es el radio-vector que indica la posición del punto arbitrario $P$ donde se evalúan dichos campos, y $\mathbf{E}_i(\mathbf{r})$ y $V_i(\mathbf{r})$ , las correspondientes contribuciones de la carga $q i$ al valor del campo eléctrico y del potencial en dicho punto. Por tanto, en el punto $O$ que coincide con el origen del sistema de referencia adoptado, se tendrá:

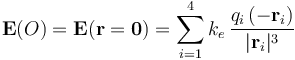
$\mathbf{E}(O)=\mathbf{E}(\mathbf{r}=\mathbf{0})=\sum_{i=1}^4k_e\!\ \frac{q_i\!\ (-\mathbf{r}_i)}{|\mathbf{r}_i|^3}$ $\Rightarrow$ $\mathbf{E}(O)=-k_e\left[\frac{q\!\ (\mathbf{r}_1+\mathbf{r}_3)}{(4a)^3}-\frac{q\!\ (\mathbf{r}_2+\mathbf{r}_4)}{(3a)^3}\right]=\mathbf{0}$

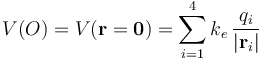
$V(O)=V(\mathbf{r}=\mathbf{0})=\sum_{i=1}^4k_e\!\ \frac{q_i}{|\mathbf{r}_i|}$ $\Rightarrow$ $V(O)=k_e\left[\frac{2\!\ q}{4a}-\frac{2\!\ q }{3a}\right]=-k_e\!\ \frac{q}{6a}$

2.2 Fuerza electrostática sobre cada carga

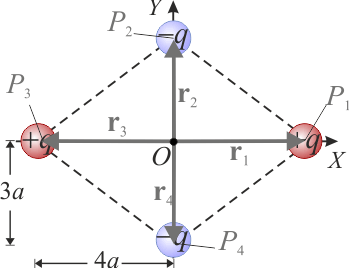
Si las cuatro cargas eléctricas que constituyen el sistema se consideran entes puntuales, cada una de ellas estará sometida exclusivamente a la acción de las otras tres. Por tanto, sobre cada carga actúa una fuerza electrostática igual a la resultante de las fuerzas que, según la ley de Coulomb, ejercen sobre ella las otras cargas que constituyen el sistema; es decir:

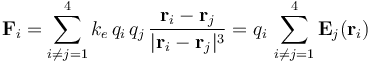
$\mathbf{F}_i=\sum_{i\neq j=1}^4k_e\!\ q_i\!\ q_j\!\ \frac{\mathbf{r}_i-\mathbf{r}_j}{|\mathbf{r}_i-\mathbf{r}_j|^3}=q_i\!\ \sum_{i\neq j=1}^4\mathbf{E}_j(\mathbf{r}_i)$

Debido a la simetría del sistema, tanto por su geometría como por los valores de las cargas eléctricas, se obtiene...

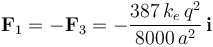
$\mathbf{F}_1=2k_eq^2\!\ \mathbf{r}_1\!\ \left[\frac{1}{(8a)^3}-\frac{1}{(5a)^3}\right]=-\mathbf{F}_3$ $\Rightarrow$ $\mathbf{F}_1=-\mathbf{F}_3=-\frac{387\!\ k_e\!\ q^2}{8000\!\ a^2}\!\ \mathbf{i}$

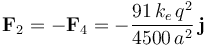
$\mathbf{F}_2=2k_eq^2\!\ \mathbf{r}_2\!\ \left[\frac{1}{(6a)^3}-\frac{1}{(5a)^3}\right]=-\mathbf{F}_4$ $\Rightarrow$ $\mathbf{F}_2=-\mathbf{F}_4=-\frac{91\!\ k_e\!\ q^2}{4500\!\ a^2}\!\ \mathbf{j}$

Es decir, cada una de las cuatro cargas es atraída por las otras tres hacia el centro $O$ de la distribución. Además, las fuerza resultante sobre las cargas positivas ( $q 1$ y $q 3$ ) es más intensa que sobre las negativas ( $q 2$ y $q 4$ ):

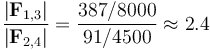
$\frac{|\mathbf{F}_{1,3}|}{|\mathbf{F}_{2,4}|}=\frac{387/8000}{91/4500}\approx 2.4$

2.3 Trabajo externo para reunir las cargas

El trabajo realizado por una fuerza “externa” para reunir las cuatro cargas, trayéndolas desde el infinito hasta los puntos $P i$ en que se hayan situadas es la energía electrostática almancenada en el sistema. Su valor es igual a la mitad de la suma de las energías potenciales que tienen cada una de las cargas, por hallarse en el campo eléctrico creado por el resto de las cargas que constituyen el sistema:

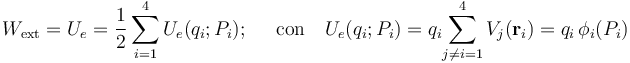
$W_\mathrm{ext}=U_e=\frac{1}{2}\sum_{i=1}^4U_e(q_i;P_i)\mathrm{;}\quad\;\;\mathrm{con}\quad U_e(q_i;P_i)=q_i\! \sum_{j\neq i=1}^4V_j(\mathbf{r}_i)=q_i\!\ \phi_i(P_i)$

Nuevamente la simetría del sistema permite reducir el número de cálculos que es necesario realizar, ya que:

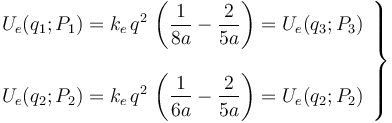
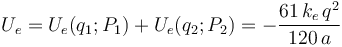
$\left.\begin{array}{l}\displaystyle U_e(q_1;P_1)=k_e\!\ q^2\!\ \left(\frac{1}{8a}-\frac{2}{5a}\right)=U_e(q_3;P_3)\\ \\ \displaystyle U_e(q_2;P_2)=k_e\!\ q^2\!\ \left(\frac{1}{6a}-\frac{2}{5a}\right)=U_e(q_2;P_2)\end{array}\right\}$ $\Rightarrow$ $U_e=U_e(q_1;P_1)+U_e(q_2;P_2)=-\frac{61\!\ k_e\!\ q^2}{120\!\ a}$

Si las cuatro cargas tienen un valor absoluto de 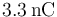$3.3\,\mathrm{nC}\,$ y la distancia $a$ es de 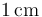$1\,\mathrm{cm}\,$ , el trabajo realizado por las fuerzas externas para reunir las cuatro cargas será:

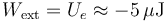
$W_\mathrm{ext}=U_e\approx -5\,\mu\mathrm{J}$

2.4 Acción sobre un dipolo puntual

Consideremos un dipolo eléctrico situado en el punto $O$ y con su momento dipolar orientado de manera que 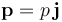$\mathbf{p}=p\!\ \mathbf{j}$ . El campo eléctrico creado por el sistema de cargas puntuales ejerce sobre el dipolo una fuerza resultante y un momento o par de fuerzas resultante. El valor de este par de fuerzas se obtiene directamente teniendo en cuenta que, si el dipolo es un ente puntual, dicho par de fuerza es igual al producto vectorial del momento dipolar del dipolo, por el campo eléctrico existente en el punto que aquél ocupa, y que es debido a otras cargas eléctricas. En este caso se tendría:

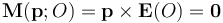
$\mathbf{M}(\mathbf{p};O)=\mathbf{p}\times\mathbf{E}(O)=\mathbf{0}$

pues, como se comprobó en el primer apartado, el campo eléctrico creado por el sistema de cuatro cargas es nulo en el centro $O$ de la distribución, donde ahora se encuentra el dipolo. Obsérvese que este resultado va a ser independiente de la orientación del dipolo. Además, si en un instante inicial éste se encuentra en reposo en dicho punto, mantendrá su orientación, al menos inicialmente.

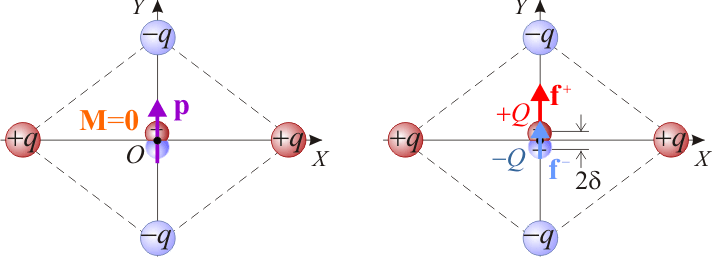
En cuanto a la fuerza resultante que actúa sobre el dipolo, podemos hacer un análisis cualitativo del sistema que nos permita saber cómo actúa sobre el dipolo cuando éste se encuentra en la posición y con la orientación anteriormente indicadas. 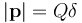Para ello, consideraremos que el dipolo está formado por sendas cargas puntuales $+ Q$ y $- Q$ , separadas una distancia $2\delta\ll a$ , y de manera que $|\mathbf{p}|=Q\delta$ . Además, dichas cargas se encontrarían en el eje $O Y$ , ambas equidistantes y muy próximas al punto $O$ . La carga $+ Q$ es atraída tanto por la $q 2$ como por la $q 4$ . Sin embargo, la carga positiva del dipolo se encuentra un poco más cerca de $q 2$ que de $q 4$ , de manera que sobre aquélla actuará una fuerza neta 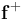$\mathbf{f}^+$ con la dirección y el sentido del vector unitario 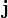$\mathbf{j}$ . Igualmente, la carga negativa del dipolo es repelida por $q 4$ con más intensidad que por $q 2$ , por estar más cerca de aquélla, de manera que también sobre $- Q$ actúa una fuerza neta 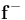$\mathbf{f}^-$ en la dirección y sentido de 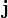$\mathbf{j}$ . Por su parte, las contribuciones de las cargas positivas del sistema ( $q 1$ y $q 3$ ) en los puntos del eje $O Y$ cancelan sus componentes en la dirección del eje $O X$ . Dichas cargas sí producen componente neta del campo en la dirección $O Y$ , pero ésta es muy poco significativa en las proximidades del punto $O$ . Por añadidura, las cargas positivas de la distribución están más alejadas del punto $O$ que las negativas, de manera que el efecto de aquéllas sobre el dipolo puede ser considerado despreciable frente al que producen $q 2$ y $q 3$ . En definitiva, podemos asegurar que la fuerza resultante sobre el dipolo es...

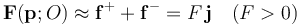
$\mathbf{F}(\mathbf{p};O)\approx \mathbf{f}^++\mathbf{f}^-=F\!\ \mathbf{j}\quad(F>0)$

Es decir, la fuerza es colineal con el momento dipolar, y tendería a mover al dipolo hacia la carga $q 2$ , situada en el punto $P 2$ .

No es complicado calcular exactamente cuanto vale la fuerza resultante que actúa sobre el dipolo de momento dipolar 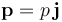$\mathbf{p}=p\!\ \mathbf{j}$ . Para ello consideramos que éste consiste en dos cargas puntuales, $+ Q$ y $- Q$ , situadas en sendos puntos dados por los rectores posición 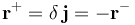$\mathbf{r}^+=\delta\!\ \mathbf{j}=-\mathbf{r}^-$ . La fuerza que actúa sobre dipolo puede obtenerse en términos del valor del campo eléctrico creado por el sistema de cuatro cargas en los dos puntos del eje $O Y$ en que se hallan las cargas que constituyen el dipolo:

$\mathbf{F}(\mathbf{p};O)=+Q\!\ \mathbf{E}(\mathbf{r}^+)+(-Q)\!\ \mathbf{E}(\mathbf{r}^-)=Q\!\ \big[\mathbf{E}(0,\delta,0)-\mathbf{E}(0,-\delta,0)\big]$

Teniendo en cuenta que el campo eléctrico en los puntos del eje $O Y$ es:

$\mathbf{E}(0,y,0)= \sum_{i=1}^4k_e\!\ \frac{q_i\!\ (y\!\ \mathbf{j}-\mathbf{r}_i)}{|y\!\ \mathbf{j}-\mathbf{r}_i|^3}=2\!\ k_e\!\ q\!\ \left[\frac{y}{(y^2+16a^2)^{3/2}}-\frac{y^2+9a^2}{(y^2-9a^2)^2}\right]\!\ \mathbf{j}$

... se obtiene:

$\mathbf{F}(\mathbf{p};O)=4\!\ k_e q \!\ \frac{Q\!\ \delta}{(\delta^2+16a^2)^{3/2}}\!\ \mathbf{j}\approx \frac{k_e\!\ q}{16\!\ a^3}\!\ \mathbf{p}$

Sistema electrostático de cuatro cargas, F2 GIA (Abr, 2013)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Campo eléctrico y potencial electrostático en el centro de la distribución

2.2 Fuerza electrostática sobre cada carga

2.3 Trabajo externo para reunir las cargas

2.4 Acción sobre un dipolo puntual

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES