Trabajo realizado para reunir cuatro cargas puntuales (F2GIA)
De Laplace
1 Enunciado
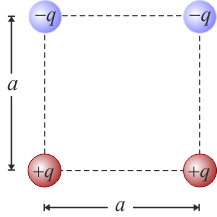
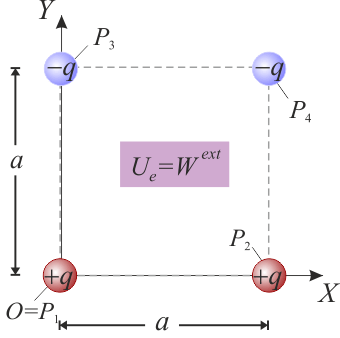
Un sistema electrostático está formado por dos cargas puntuales de valor + q y otras dos − q, situadas en los vértices de un cuadrado de lado a. Las cargas están dispuestas de manera que en los extremos de cada diagonal del cuadrado hay cargas de distinto signo, tal como se muestra en la figura. Calcular el trabajo externo que ha sido necesario realizar para configurar dicho sistema trayendo las cargas desde el infinito.
2 Solución
Para constituir el sistema electrostático bajo estudio procedereremos a traer las cargas, una a una, siguiendo una secuencia de cuatro procesos. En cada uno de ellos, la carga que se traslada estará sometida a la fuerza externa y a la fuerza que ejerce sobre ella el campo eléctrico creado por las cargas traídas previamente. Además, procuraremos que dichos procesos sean (casi)estacionarios. Es decir, procesos (casi)ideales en los que la disipación de energía por fricción o rozamiento es (casi)nula, y la energía cinética del sistema no sufre variaciones apreciables. Por tanto, en cada instante de tiempo se tendrá que los trabajos infinitesimales realizados por la fuerza externa aplicada y por el campo eléctrico que actúa sobre la carga qi transportada, son opuestos. Y como la fuerza realizada por un campo eléctrico creado por cargas en reposo es conservativa, se tendrá que el trabajo elemental de la fuerza externa va a coincidir con la variación que experimenta la energía potencial de la partícula cargada qial desplazarse una cantidad infinitesimal en el seno del campo eléctrico creado por las cargas previamente reunidas:
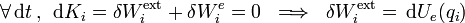
En consecuencia, el trabajo total externo 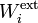 realizado para traer la carga qi desde el infinito hasta su posición final Pi será igual al valor de la energía potencial de la carga cuando se halla localizada en dicho punto. Y si la carga es puntual, esta energía potencial es igual al producto de la carga por el valor en Pi del potencial electrostático creado por las cargas traidas anteriormente. Es decir:
realizado para traer la carga qi desde el infinito hasta su posición final Pi será igual al valor de la energía potencial de la carga cuando se halla localizada en dicho punto. Y si la carga es puntual, esta energía potencial es igual al producto de la carga por el valor en Pi del potencial electrostático creado por las cargas traidas anteriormente. Es decir:
![W_i^\mathrm{ext}=U_e(q_i;P_i)=q_i\!\ \left[V_1(P_i)+\ldots+V_{i-1}(P_i)\right]](/wiki/images/math/4/e/3/4e3a2ff2b10166a18fd1697add718779.png)
Traigamos, en primer lugar, una de las cargas positivas. Obsérvese que como no hay cargas previas en el sistema, sobre esta q1 = + q no actúa fuerza eléctrica alguna (consideramos que se ecuentra fuera del radio de acción de cualquier otra carga), ni tampoco "trabajo eléctrico" por lo que, si q1 viene hasta el punto O = P1 mediante un proceso estacionario, no será necesario realizar ningún trabajo externo. O desde otro punto de vista: como aún no hay cargas previas, cuando traemos la carga q1 al punto P1 el valor del potencial electrostático en cualquier punto del espacio es nulo, por lo que,
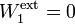
Pero una vez traida, la carga crea una "perturbación" de naturaleza eléctrica que, si la consideramos situada en el origen del sistema de referencia, puede ser descrita en términos de la siguiente expresión del potencial electrostático:
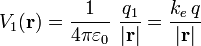
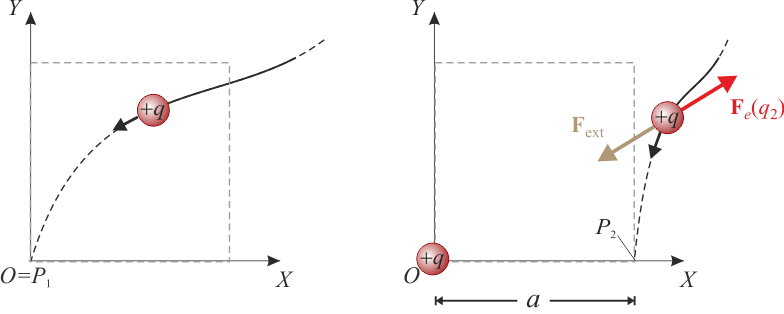
Traemos ahora la segunda carga positiva, q2 = + q, hasta el punto P2, que se halla a una distancia a de la primera. El trabajo externo necesario para lleva a cabo este proceso en condiciones estacionarias es:
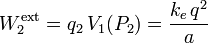
Asimismo, a partir de que esta carga ocupe la posición P2 (que respecto del origen de coordenadas vendrá dada por el radiovector \mathbf{r}_2}), provocará una nueva perturbación dada por el potencial
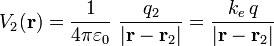
cuyo valor en cada punto del espacio es inversamente proporcional a la distancia que los separa de P2. Este potencial eléctrostatico se superpone al generado por la primera carga traída a O = P1, de manera que al traer la carga q3 = − q al punto P3, a una distancia a de P1 y 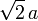 , respecto de P2, la fuerza externa habrá realizado un trabajo:
, respecto de P2, la fuerza externa habrá realizado un trabajo:
![W_3^\mathrm{ext}=q_3\!\ \left[V_1(P_3)+V_2(P_3)\right]=-k_e\!\ q^2\ \left(\frac{1}{a}+\frac{1}{\sqrt{2}\!\ a}\right)](/wiki/images/math/9/4/3/943cfd2155a31bb8d0b39600c2b7c6be.png)
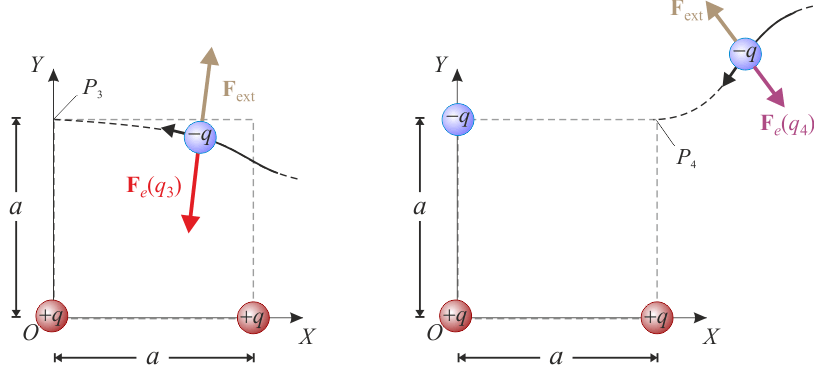
Nuevamente, esta tercera carga en P3, cuya posición viene dada por el radiovector 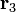 ), produce un potencial electrostático descrito por la función de campo:
), produce un potencial electrostático descrito por la función de campo:
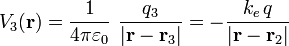
que se superpondrá a las perturbaciones creadas por las anteriores carga q1 y q2. De esta forma, cuando se proceda a traer la carga q4 = − q desde el infinito hasta la posición P4 siguiendo un proceso estacionario, la fuerza externa habrá realizado un trabajo:
![W_4^\mathrm{ext}=q_4\!\ \left[V_1(P_4)+V_2(P_4)+V_3(P_4)\right]=-k_e\!\ q \ \left(\frac{q}{a}+\frac{q}{\sqrt{2}\!\ a}-\frac{q}{a}\right)=-\frac{k_e\!\ q^2}{\sqrt{2}\!\ a}](/wiki/images/math/0/7/5/07558883e4cad39f575b6a3d76e43d80.png)
El trabajo total realizado por las fuerzas externas en estos cuatro procesos estacionarios es:
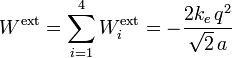
Obsérvese que en cada proceso estacionario el trabajo parcial 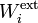 es igual a la variación sufrida por la energía potencia electrostática de la carga qi, y que ésta es una magnitud que sólo depende de las cargas y de las posiciones inicial (en el infinito) y final (en Pi) de la carga. Por tanto, el trabajo total realizado por las fuerza externas para reunir las cuatro cargas, sólo dependerá de los valores de éstas y de las posiciones que ocupen, y será independiente, por tanto, del orden en que se realicen los cuatro procesos anteriores.
es igual a la variación sufrida por la energía potencia electrostática de la carga qi, y que ésta es una magnitud que sólo depende de las cargas y de las posiciones inicial (en el infinito) y final (en Pi) de la carga. Por tanto, el trabajo total realizado por las fuerza externas para reunir las cuatro cargas, sólo dependerá de los valores de éstas y de las posiciones que ocupen, y será independiente, por tanto, del orden en que se realicen los cuatro procesos anteriores.
En consecuencia, este trabajo externo realizado en condiciones estacionarias es una función de estado del sistema, que denominaremos energía electrostática del sistema, Ue. Ha de advertirse que no se debe confundir con la energía potencial electrostática de una carga puntual situado en un punto donde hay un campo eléctrico/potencial electrostático. Puede comprobarse que la energía electrostatica de un sistema de cargas puntuales es igual a la semisuma de las energías potenciales de cada una de las cargas al hallarse sometida a la acción del resto. En el sistema bajo estudio, se tendría:
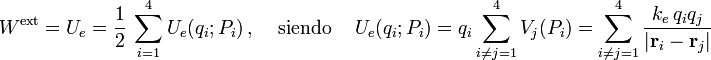
El ejercicio puede resolverse también aplicando directamente estos resultados.
Por otra parte, que el trabajo total realizado por las fuerzas externas sea negativo quiere decir que el trabajo neto necesario para configurar el sistema bajo estudio, ha sido realizado por el campo eléctrico creado por las propias cargas que lo constituyen.