Problemas de procesos en gases ideales (GIA)
De Laplace
(→Trabajo en un ciclo de un gas perfecto) |
(→Expansión isoterma y adiabática) |
||
| Línea 24: | Línea 24: | ||
== [[ Comparación_de_un_proceso_isotérmico_y_uno_adiabático | Expansión isoterma y adiabática ]] == | == [[ Comparación_de_un_proceso_isotérmico_y_uno_adiabático | Expansión isoterma y adiabática ]] == | ||
| + | Un gas ideal monoatómico ocupa un volumen de <math>4\,\mathrm{m^3}</math> | ||
| + | a la presión de <math>8\,\mathrm{atm}</math> y a la temperatura de | ||
| + | <math>400\,\mathrm{K}</math>. El gas se expande hasta la presión final de | ||
| + | <math>1\,\mathrm{atm}</math> mediante un proceso cuasiestático. Calcule el | ||
| + | trabajo realizado, el calor absorbido y la variación de energía interna en | ||
| + | los siguientes casos: | ||
| + | |||
| + | #Expansión isoterma. | ||
| + | #Expansión adiabática. | ||
== [[ Comparación_de_un_proceso_isotérmico_y_uno_adiabático | Proceso isotérmico y adiabático en un gas perfecto ]] == | == [[ Comparación_de_un_proceso_isotérmico_y_uno_adiabático | Proceso isotérmico y adiabático en un gas perfecto ]] == | ||
== [[ Expansión_adiabática_no_cuasiestática | Expansión adiabática no cuasiestática de un gas ideal ]] == | == [[ Expansión_adiabática_no_cuasiestática | Expansión adiabática no cuasiestática de un gas ideal ]] == | ||
Revisión de 12:31 25 may 2011
1 Trabajo en tres procesos que unen dos estados
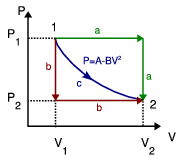
Calcula el trabajo realizado sobre un fluido que se expande en los tres procesos entre los mismos estados inicial y final indicados en la figura. En el proceso c, que es cuasi-estático, se tiene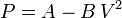 
, con 
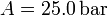y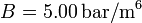 
. Los volúmenes inicial y final son 
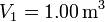y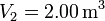 
.
2 Temperatura de una llama
Para averiguar la temperatura de una llama se calienta con ella un trozo de hierro de 200 g que, a continuación, se introduce en un calorímetro que contiene un litro de agua. Se observa que la temperatura de ésta aumenta de 18.0 a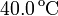 
. ¿Cuál es la temperatura de la llama?
Datos: capacidad calorífica del calorímetro: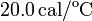 
, 
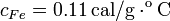, calor específico del agua líquida: 
.
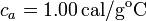3 Estado final de una mezcla de hielo y vapor de agua
En un calorímetro que contiene 200 g de hielo a -8.00 °C se introducen 50.0 g de vapor de agua a 100 °C. El equivalente en agua del calorímetro es 20.0 g. Determina el estado final de la mezcla.
Datos: calor específico del hielo: 0.500 cal/g °C; entalpía de fusión del hielo: 80.0cal/g; entalpía de vaporización del agua: 537 cal/g
4 Trabajo en un ciclo de un gas perfecto
Las condiciones iniciales del estado de un gas perfecto son: V=4.00 l, P=2.00 atm, t = 27.0o C. Se dilata el gas a presión constante hasta duplicar su volumen. A continuación se comprime isotérmicamente hasta recuperar el volumen inicial. Finalmente se enfría a volumen constante hasta su presión inicial.
- Dibuja el ciclo en un diagrama PV.
- Calcula el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos.
5 Expansión isoterma y adiabática
Un gas ideal monoatómico ocupa un volumen de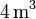 
a la presión de 
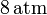y a la temperatura de
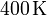. El gas se expande hasta la presión final de
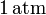mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
- Expansión isoterma.
- Expansión adiabática.
