Trabajo en tres procesos que unen dos estados GIA
De Laplace
Contenido |
1 Enunciado
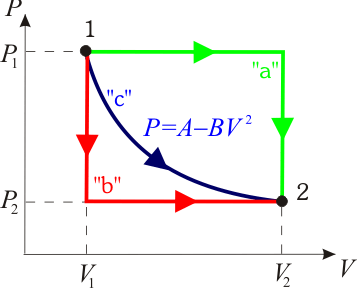
Calcula el trabajo realizado sobre un fluido que se expande en los tres procesos entre los mismos estados inicial y final indicados en la figura. En el proceso c, que es cuasi-estático, se tiene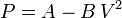 
, con 
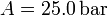y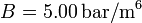 
. Los volúmenes inicial y final son 
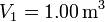y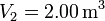 
.
2 Solución
Las presiones de los estados 1 y 2 pueden obtenerse a partir de la ecuación de estado del proceso 3.
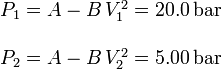
Ahora podemos calcular el trabajo en los tres procesos.
2.1 Proceso a
Este proceso consta de dos subprocesos, uno a presión constante P1 y otro a volumen constante V2. En el proceso a presión constante el trabajo es
Wa1 = − P1(V2 − V1)
mientras que en el proceso a volumen constante el trabajo es cero pues el volumen no cambia. El trabajo total es la suma del trabajo en cada subproceso.
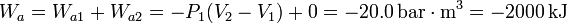
2.2 Proceso b
Este proceso consta de dos subprocesos, uno a volumen constante V1 y otro a proceso constante P2. En el proceso a volumen constante el trabajo es cero pues el volumen no cambia, mientras que en el proceso a presión constante el trabajo es
Wb2 = − P2(V2 − V1)
El trabajo total es la suma del trabajo en cada subproceso.
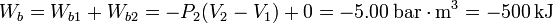
2.3 Proceso c
En este caso la presión varía durante el proceso según la ecuación de estado dada en el enunciado. El trabajo es
![W_c = -\int\limits_1^2 P\,\mathrm{d}V =
-\int\limits_1^2 \left(A-B\,V^2\right) \,\mathrm{d}V=
-\left[A\,V - \dfrac{B\,V^3}{3}\right]_{V_1}^{V_2}=
-1333\,\mathrm{kJ}](/wiki/images/math/0/3/b/03b2b15cbdecb86818bd869ed101f913.png)
