Expansión adiabática no cuasiestática

De Laplace

Contenido

1 Enunciado
2 Temperatura final
3 Variación de energía interna
4 Trabajo realizado por el gas
5 Comparación con un proceso cuasiestático

1 Enunciado

4 moles de nitrógeno están a 25 $o$ C y 30 atm. Se pasa bruscamente la presión hasta un valor de 10 atm mediante una expansión adiabática del gas contra una presión exterior constante de 10 atm. El proceso no es cuasiestático. Calcule

La temperatura final del gas suponiendo que la ecuación de estado de los gases ideales es aplicable a los estados inicial y final.
La variación de energía interna.
El trabajo realizado sobre el gas.
Compare con las mismas magnitudes en un proceso adiabático cuasiestático que expanda el gas hasta la misma presión final de 10 atm.

2 Temperatura final

En este problema no se puede aplicar la ecuación de Poisson para relacionar los estados inicial y final, pues el proceso no es cuasiestático. Los datos que tenemos del proceso son

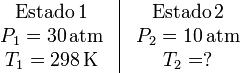
$\begin{array}{c|c} \begin{array}{c} \mathrm{Estado\,1}\\ P_1=30\,\mathrm{atm}\\ T_1=298\,\mathrm{K} \end{array}& \begin{array}{c} \mathrm{Estado\,2}\\ P_2=10\,\mathrm{atm}\\ T_2= ? \end{array} \end{array}$

Como la expansión se realiza contra una presión constante $P ext = P 2$ , podemos calcular el trabajo realizado sobre el gas

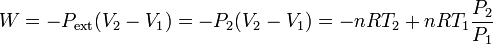
$W=-P_{\mathrm{ext}}(V_2-V_1)=-P_2(V_2-V_1)=-nRT_2+nRT_1\frac{P_2}{P_1}$

Hemos usado la ecuación de estado para expresar el trabajo en función de las temperaturas y las presiones.

Por otro lado, al ser el proceso adiabático la variación de energía interna es igual al trabajo. La variación de energía se puede expresar también en función de la diferencia de temperaturas y del calor específico a volumen constante, que al ser un gas ideal diatómico vale $c v = 5 R / 2$ . Con todo esto tenemos

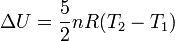
$\Delta U=\frac{5}{2}nR(T_2-T_1)$

Igualando las dos expresiones obtenemos

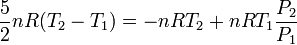
$\frac{5}{2}nR(T_2-T_1)=-nRT_2+nRT_1\frac{P_2}{P_1}$

Despejando obtenemos

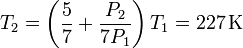
$T_2=\left(\frac{5}{7}+\frac{P_2}{7P_1}\right)T_1=227\,\mathrm{K}$

3 Variación de energía interna

La variación de energía interna es

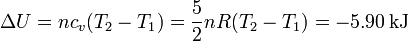
$\Delta U = nc_v(T_2-T_1)=\frac{5}{2}nR(T_2-T_1)=-5.90\,\mathrm{kJ}$

4 Trabajo realizado por el gas

Como es un proceso adiabático, tenemos

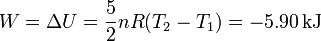
$W=\Delta U = \frac{5}{2}nR(T_2-T_1)=-5.90\,\mathrm{kJ}$

5 Comparación con un proceso cuasiestático

Si la expansión fuese cuasiestática, en todo momento la presión exterior sería igual a la presión en el gas. En este caso podríamos aplicar la ecuación de Poisson para relacionar los estados inicial y final

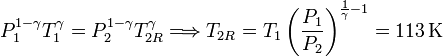
$P_1^{1-\gamma}T_1^{\gamma}=P_{2}^{1-\gamma}T_{2R}^{\gamma}\Longrightarrow T_{2R}=T_1\left(\frac{P_1}{P_2}\right)^{\frac{1}{\gamma}-1}=113\,\mathrm{K}$

La variación de energía interna y, por tanto, el trabajo realizado por el gas serían

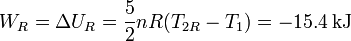
$W_R=\Delta U_R=\frac{5}{2}nR(T_{2R}-T_1)=-15.4\,\mathrm{kJ}$

Podemos ver que al realizar el proceso de modo no cuasiestático el sistema proporciona menos trabajo del que haría si el proceso fuese cuasiestático. Veremos en el tema siguiente que esto está relacionado con el Segundo Principio de la Termodinámica y la irreversibilidad del proceso.

Expansión adiabática no cuasiestática

De Laplace

Contenido

1 Enunciado

2 Temperatura final

3 Variación de energía interna

4 Trabajo realizado por el gas

5 Comparación con un proceso cuasiestático

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES