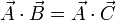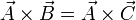Problemas de vectores libres (G.I.A.)
De Laplace
(→Producto vectorial de dos vectores) |
(→Ejercicios del boletín de problemas 1 (2017/18)) |
||
| (29 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | ==[[ | + | = Ejercicios del boletín de problemas 1 (2018/19) = |
| - | + | ||
| + | ==[[Cuestión de álgebra vectorial, Noviembre 2012 (F1 GIA)|Posición de vértices y volumen de un paralelepípedo]]== | ||
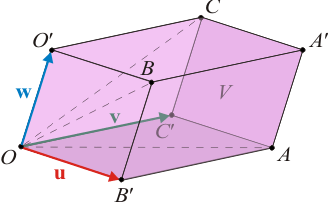
| + | [[Archivo:paralelep_PC1_0.gif|right]]Los puntos <math>O</math>, <math>A</math>, <math>B</math> y <math>C</math> son vértices no contiguos de un paralelepípedo, de manera que <math>O</math> y <math>A</math> se encuentran en un plano distinto al que contiene a <math>B</math> y <math>C</math>. Las coordenadas de estos puntos en un sistema de | ||
| + | referencia cartesiano son: | ||
| + | |||
| + | <center><math>O(0, 0, 0)\mathrm{;}\quad A(\sqrt{3} + 1, 0,0)\mathrm{;}\quad B(1, 0, 1)\mathrm{;}\quad C(\sqrt{3}, 2, 1)\mathrm{,} | ||
| + | </math></center> | ||
| + | |||
| + | medidas en unidades de longitud. Determine las componentes cartesianas de los vectores | ||
| + | <center><math>\vec{u}=\overrightarrow{OB}^\prime\mathrm{;}\quad\vec{v}=\overrightarrow{OC}^\prime\mathrm{;}\quad\vec{w}=\overrightarrow{OO}^\prime.</math></center> | ||
| + | y calcule el volumen del paralelepípedo. | ||
==[[Componentes_cartesianas_de_un_vector_(G.I.A.)|Componentes cartesianas de un vector]]== | ==[[Componentes_cartesianas_de_un_vector_(G.I.A.)|Componentes cartesianas de un vector]]== | ||
| - | + | Calcule las componentes cartesianas de un vector <math>\vec{a}</math> con módulo de 13.0 unidades que forma un | |
| - | ángulo <math>\gamma=22.6^{\circ}</math> con el eje <math> | + | ángulo <math>\gamma=22.6^{\circ}</math> con el eje <math>OZ</math> y cuya proyección en el plano <math>OXY</math> forma un ángulo |
| - | <math>\alpha=37.0^{\circ}</math> con el eje <math> | + | <math>\alpha=37.0^{\circ}</math> con el eje <math>OX</math>. Calcule también los ángulos con los ejes <math>OX</math> y <math>OY</math>. |
| + | |||
| + | ==[[Proyección de la aceleración de la gravedad en cuatro diedros (G.I.C.) |Proyección de la aceleración de la gravedad en cuatro diedros]]== | ||
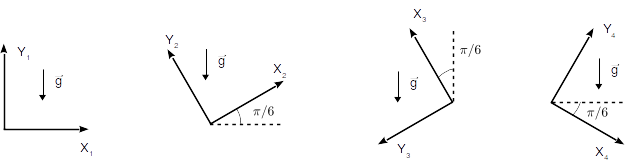
| + | Cerca de la superficie terrestre la aceleración de la gravedad se puede representar como un vector <math>\vec{g} </math> de módulo <math>|g| = 9.81 \,\mathrm{m/s^2}</math> , dirección vertical y sentido hacia abajo. Calcule las componentes de <math>\vec{g} </math> en los cuatro sistemas de referencia de la figura. | ||
| + | [[Imagen:Proyeccion_gravedad_enunciado.png|center]] | ||
| + | |||
| + | == [[ Ángulo que forman dos vectores (G.I.A.) | Ángulo que forman dos vectores ]] == | ||
| + | Calcule el angulo que forman los vectores | ||
| + | <math>\vec{a} = 2\,\vec{\imath} + 3\,\vec{\jmath} - \vec{k}</math> | ||
| + | y | ||
| + | <math>\vec{b} = -\vec{\imath} + \vec{\jmath} +2\, \vec{k}</math>. Obtenga también los cosenos directores de ambos vectores. | ||
==[[Diagonales_de_un_rombo_(G.I.A.)|Diagonales de un rombo]]== | ==[[Diagonales_de_un_rombo_(G.I.A.)|Diagonales de un rombo]]== | ||
| - | Usando el álgebra vectorial, | + | Usando el álgebra vectorial, demuestre que las diagonales de un rombo |
se cortan en ángulo recto. | se cortan en ángulo recto. | ||
==[[Ángulo_capaz_de_90_(G.I.A.)|Ángulo capaz de 90<sup>o</sup>]]== | ==[[Ángulo_capaz_de_90_(G.I.A.)|Ángulo capaz de 90<sup>o</sup>]]== | ||
Dada una circunferencia de centro <math>O</math> y radio <math>R</math>, y un diámetro | Dada una circunferencia de centro <math>O</math> y radio <math>R</math>, y un diámetro | ||
| - | <math>\overline{AB}</math> cualquiera, | + | <math>\overline{AB}</math> cualquiera, demuestre que las cuerdas |
<math>\overline{PA}</math> y <math>\overline{PB}</math> se cortan perpendicularmente,para | <math>\overline{PA}</math> y <math>\overline{PB}</math> se cortan perpendicularmente,para | ||
todo punto <math>P</math> perteneciente a la circunferencia (arco capaz | todo punto <math>P</math> perteneciente a la circunferencia (arco capaz | ||
| Línea 21: | Línea 41: | ||
==[[Producto_vectorial_de_dos_vectores_(G.I.A.)|Producto vectorial de dos vectores]]== | ==[[Producto_vectorial_de_dos_vectores_(G.I.A.)|Producto vectorial de dos vectores]]== | ||
| - | + | Calcule el producto vectorial de los vectores <math>\vec{a} = 2\,\vec{\imath} + 3\,\vec{\jmath} - \vec{k}</math> | |
| + | y | ||
| + | <math>\vec{b} = -\vec{\imath} + \vec{\jmath} +2\, \vec{k}</math>, así como el área del triángulo que forman. Considere que las componentes vienen dadas en metros. | ||
==[[Teoremas_del_seno_y_del_coseno_(G.I.A.) |Teoremas del seno y del coseno]]== | ==[[Teoremas_del_seno_y_del_coseno_(G.I.A.) |Teoremas del seno y del coseno]]== | ||
| - | Usando el álgebra vectorial, | + | Usando el álgebra vectorial, demuestre el teorema del seno y el teorema del coseno para triángulos planos. |
| + | |||
| + | ==[[Cuestión de álgebra vectorial, Noviembre 2011 |Rombo situado en el espacio]]== | ||
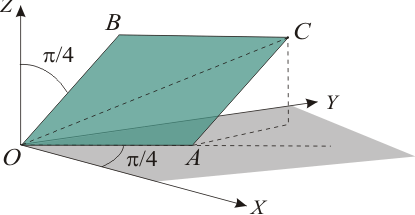
| + | [[Archivo:algvec_nov_11.gif|right]]El rombo <math>OACB</math> tiene sus lados de longitud unidad y su | ||
| + | área es igual a <math>\displaystyle\sqrt{3}/2</math>. Su lado <math>OA</math> se encuentra en el plano | ||
| + | <math>OXY</math> de un sistema de referencia cartesiano, formando un ángulo de | ||
| + | <math>\pi/4</math> con el eje <math>OX</math>. El lado <math>OB</math> forma un ángulo de <math>\pi/4</math> | ||
| + | con el eje <math>OZ</math>. | ||
| + | |||
| + | # Calcular la longitud de la diagonal <math>OC</math> | ||
| + | # Determinar las coordenads cartesianas del vértice <math>C</math> | ||
| + | |||
| + | ==[[Volumen de un paralelepípedo_(G.I.A.)|Volumen de un paralelepípedo]]== | ||
| + | Calcule el volumen del paralelepípedo que tiene como aristas los | ||
| + | vectores <math>\overrightarrow{OA}</math>, <math>\overrightarrow{OB}</math> y <math>\overrightarrow{OC}</math>. Las coordenadas | ||
| + | cartesianas de dichos puntos vienen dadas por las ternas | ||
| + | <math>O(1,0,2)</math>, <math>A(3,2,4)</math>, <math>B(2,6,8) </math> y <math> C(2,-3,1)</math> (unidades | ||
| + | medidas en metros). | ||
| + | |||
| + | ==[[Producto_mixto_nulo_(G.I.A.)|Producto mixto nulo]]== | ||
| + | |||
| + | Dados los vectores <math>\vec{A}</math>, <math>\vec{B}</math> y <math>\vec{C}</math>, | ||
| + | demuestre que la relación | ||
| + | <math>\vec{A} \cdot ( \vec{B} \times \vec{C})=0</math> | ||
| + | se cumple en cualquiera de los siguientes supuestos: | ||
| + | #Los tres vectores son colineales. | ||
| + | #Dos de los vectores son colineales. | ||
| + | #<math>\vec{A}</math>, <math>\vec{B}</math> y <math>\vec{C}</math> no son colineales pero sí coplanarios. | ||
| + | |||
| + | = Otros ejercicios de vectores libres = | ||
| + | |||
| + | ==[[Suma_y_diferencia_de_vectores_(G.I.A.)|Suma y diferencia de vectores]]== | ||
| + | El vector <math>\vec{a}</math> tiene un módulo de 6.00 unidades y forma un ángulo de <math>36.0^{\circ}</math> con el eje <math>X</math>, mientras que el vector <math>\vec{b}</math> tiene un módulo de 7.00 unidades y apunta en la dirección negativa del eje <math>X</math>. Calcula la suma y la diferencia de estos dos vectores haciendo uso de los teoremas del seno y del coseno. | ||
==[[Vértices_de_un_tetraedro_(G.I.A.)|Vértices de un tetraedro]]== | ==[[Vértices_de_un_tetraedro_(G.I.A.)|Vértices de un tetraedro]]== | ||
| + | [[Imagen:F1_GIA_b02_p08_a.png|right]] | ||
| + | Los puntos <math>O</math>, <math>A</math>, <math>B</math> y <math>C</math> son los vértices del tetraedro | ||
| + | regular cuyas caras son triángulos equiláteros con lados de longitud | ||
| + | <math>\lambda</math>. A partir de las aristas de dicho tetraedro se definen los | ||
| + | siguientes vectores libres: | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{lllll} | ||
| + | \vec{\omega}_1=\overrightarrow{OA} && \vec{\omega}_2=\overrightarrow{AB} && \vec{\omega}_3=\overrightarrow{BO}\\ | ||
| + | \vec{\omega}_4=\overrightarrow{OC} && \vec{\omega}_5=\overrightarrow{AC} && \vec{\omega}_6=\overrightarrow{BC} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Para describirlos analíticamente se adopta un sistema de | ||
| + | referencia cartesiano <math>OXYZ</math>, tal que la cara <math>OAB</math> del tetraedro | ||
| + | está contenida en el plano <math>OXY</math>, y el vértice <math>B</math> es un punto del | ||
| + | eje <math>OY</math> (ver figura). Utilizando las herramientas del Álgebra | ||
| + | Vectorial, determina las coordenadas cartesianas de los vértices del | ||
| + | tetraedro. | ||
| + | |||
| + | ==[[Volumen de un tetraedro_(G.I.A.)|Volumen de un tetraedro]]== | ||
| + | Halla el volumen de un tetraedro del cuál se sabe que las coordenadas | ||
| + | cartesianas de dos de sus vértices se corresponden con las ternas | ||
| + | <math>A(0,1,1)</math> y <math>B(2,-1,2)</math>, y que dos de las aristas que concurren en <math>B</math> | ||
| + | están definidas por los vectores libres <math>\vec{v}_1= 2 \vec{\imath} - 3\vec{\jmath} + \vec{k}</math> y | ||
| + | <math>\vec{v}_2 = 4 \vec{k}</math> (las coordenadas están en metros). | ||
| + | |||
| + | ==[[Distancia de un punto a un plano_(G.I.A.)|Distancia de un punto a un plano]]== | ||
| + | |||
| + | Encuentra la ecuación del plano perpendicular al vector libre <math>\vec{a} = 2\vec{\imath} +3\vec{\jmath} + 6\vec{k}</math> y que contiene a un punto <math>P</math>, cuya posición respecto del origen de un sistema de referencia <math>OXYZ</math> viene dada por el radio vector <math>\vec{r}=\vec{\imath}+5\vec{\jmath}+3\vec{k}</math>. Calcula la distancia que separa al origen <math>O</math> de dicho plano (todas las distancias están dadas en metros). | ||
==[[Distancia mínima entre dos rectas]]== | ==[[Distancia mínima entre dos rectas]]== | ||
Hallar la menor distancia entre las rectas <math>\Delta(A,B)</math> y <math>\Gamma(C,D)</math>, y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas <math>A(1,-2,-1)</math> y <math>B(4,0,-3)</math>, para el caso de <math>\Delta</math>, y <math>C(1,2,-1)</math> y <math>D(2,-4,-5)</math>, para la recta <math>\Gamma.</math> | Hallar la menor distancia entre las rectas <math>\Delta(A,B)</math> y <math>\Gamma(C,D)</math>, y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas <math>A(1,-2,-1)</math> y <math>B(4,0,-3)</math>, para el caso de <math>\Delta</math>, y <math>C(1,2,-1)</math> y <math>D(2,-4,-5)</math>, para la recta <math>\Gamma.</math> | ||
| + | |||
| + | ==[[Condiciones sobre producto escalar y vectorial_(G.I.A.)|Condiciones sobre producto escalar y vectorial]]== | ||
| + | |||
| + | Demuestra que si se cumplen simultáneamente las condiciones | ||
| + | #<math>\vec{A}\cdot \vec{B} = \vec{A}\cdot \vec{C}</math> | ||
| + | #<math>\vec{A}\times \vec{B} = \vec{A}\times \vec{C}</math> | ||
| + | |||
| + | siendo <math>\vec{A} \neq 0</math>, entonces <math>\vec{B}= \vec{C}</math>; | ||
| + | pero si sólo se cumple una de ellas, entonces <math>\vec{B} \neq \vec{C}</math>. | ||
| + | |||
| + | ==[[ Derivada de un vector (G.I.C.)| Derivada de un vector]] == | ||
| + | Un punto recorre una circunferencia de radio <math>R</math>, de modo que en cada | ||
| + | instante el vector que une el centro de la circunferencia con el punto forma un ángulo <math>\alpha</math> con el eje <math>OX</math>. | ||
| + | #Encuentra la expresión del vector de posición del punto en función del ángulo <math>\alpha</math>. | ||
| + | #Encuentra la expresión del vector de posición del punto en función del ángulo <math>\alpha</math>. | ||
| + | # Si el ángulo <math>\alpha</math> depende del tiempo como <math>\alpha=\omega t</math>, calcula la derivada del vector de posición respecto del tiempo. | ||
| + | |||
| + | == [[Recta soporte de un vector deslizante (G.I.C.) | Recta soporte de un vector deslizante]]== | ||
| + | Un vector deslizante tiene como cursor el vector libre cursor <math>\vec{a} = \vec{\imath}+\vec{\jmath} - 2\vec{k}</math> y su momento respecto al origen de coordenadas es <math>\overrightarrow{M}_O=\vec{\imath}+\vec{\jmath}+\vec{k}</math>. Encuentra la ecuación vectorial de la recta soporte del vector deslizante. | ||
última version al 18:01 17 sep 2018
1 Ejercicios del boletín de problemas 1 (2018/19)
1.1 Posición de vértices y volumen de un paralelepípedo
Los puntos O, A, B y C son vértices no contiguos de un paralelepípedo, de manera que O y A se encuentran en un plano distinto al que contiene a B y C. Las coordenadas de estos puntos en un sistema dereferencia cartesiano son:
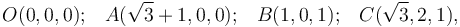
medidas en unidades de longitud. Determine las componentes cartesianas de los vectores
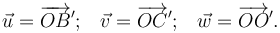
y calcule el volumen del paralelepípedo.
1.2 Componentes cartesianas de un vector
Calcule las componentes cartesianas de un vector  con módulo de 13.0 unidades que forma un
ángulo
con módulo de 13.0 unidades que forma un
ángulo 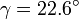 con el eje OZ y cuya proyección en el plano OXY forma un ángulo
con el eje OZ y cuya proyección en el plano OXY forma un ángulo
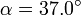 con el eje OX. Calcule también los ángulos con los ejes OX y OY.
con el eje OX. Calcule también los ángulos con los ejes OX y OY.
1.3 Proyección de la aceleración de la gravedad en cuatro diedros
Cerca de la superficie terrestre la aceleración de la gravedad se puede representar como un vector 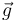 de módulo
de módulo 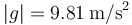 , dirección vertical y sentido hacia abajo. Calcule las componentes de
, dirección vertical y sentido hacia abajo. Calcule las componentes de 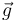 en los cuatro sistemas de referencia de la figura.
en los cuatro sistemas de referencia de la figura.
1.4 Ángulo que forman dos vectores
Calcule el angulo que forman los vectores
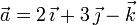 y
y
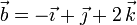 . Obtenga también los cosenos directores de ambos vectores.
. Obtenga también los cosenos directores de ambos vectores.
1.5 Diagonales de un rombo
Usando el álgebra vectorial, demuestre que las diagonales de un rombo se cortan en ángulo recto.
1.6 Ángulo capaz de 90o
Dada una circunferencia de centro O y radio R, y un diámetro
 cualquiera, demuestre que las cuerdas
cualquiera, demuestre que las cuerdas
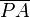 y
y 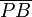 se cortan perpendicularmente,para
todo punto P perteneciente a la circunferencia (arco capaz
de 90o).
se cortan perpendicularmente,para
todo punto P perteneciente a la circunferencia (arco capaz
de 90o).
1.7 Producto vectorial de dos vectores
Calcule el producto vectorial de los vectores 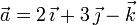 y
y
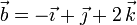 , así como el área del triángulo que forman. Considere que las componentes vienen dadas en metros.
, así como el área del triángulo que forman. Considere que las componentes vienen dadas en metros.
1.8 Teoremas del seno y del coseno
Usando el álgebra vectorial, demuestre el teorema del seno y el teorema del coseno para triángulos planos.
1.9 Rombo situado en el espacio
El rombo OACB tiene sus lados de longitud unidad y suárea es igual a 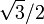 . Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
. Su lado OA se encuentra en el plano
OXY de un sistema de referencia cartesiano, formando un ángulo de
π / 4 con el eje OX. El lado OB forma un ángulo de π / 4
con el eje OZ.
- Calcular la longitud de la diagonal OC
- Determinar las coordenads cartesianas del vértice C
1.10 Volumen de un paralelepípedo
Calcule el volumen del paralelepípedo que tiene como aristas los
vectores  ,
, 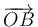 y
y  . Las coordenadas
cartesianas de dichos puntos vienen dadas por las ternas
O(1,0,2), A(3,2,4), B(2,6,8) y C(2, − 3,1) (unidades
medidas en metros).
. Las coordenadas
cartesianas de dichos puntos vienen dadas por las ternas
O(1,0,2), A(3,2,4), B(2,6,8) y C(2, − 3,1) (unidades
medidas en metros).
1.11 Producto mixto nulo
Dados los vectores  ,
,  y
y  ,
demuestre que la relación
,
demuestre que la relación
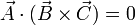 se cumple en cualquiera de los siguientes supuestos:
se cumple en cualquiera de los siguientes supuestos:
- Los tres vectores son colineales.
- Dos de los vectores son colineales.
 ,
,  y
y  no son colineales pero sí coplanarios.
no son colineales pero sí coplanarios.
2 Otros ejercicios de vectores libres
2.1 Suma y diferencia de vectores
El vector  tiene un módulo de 6.00 unidades y forma un ángulo de
tiene un módulo de 6.00 unidades y forma un ángulo de 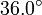 con el eje X, mientras que el vector
con el eje X, mientras que el vector  tiene un módulo de 7.00 unidades y apunta en la dirección negativa del eje X. Calcula la suma y la diferencia de estos dos vectores haciendo uso de los teoremas del seno y del coseno.
tiene un módulo de 7.00 unidades y apunta en la dirección negativa del eje X. Calcula la suma y la diferencia de estos dos vectores haciendo uso de los teoremas del seno y del coseno.
2.2 Vértices de un tetraedro
Los puntos O, A, B y C son los vértices del tetraedro regular cuyas caras son triángulos equiláteros con lados de longitud λ. A partir de las aristas de dicho tetraedro se definen los siguientes vectores libres:
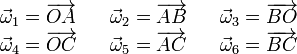
Para describirlos analíticamente se adopta un sistema de referencia cartesiano OXYZ, tal que la cara OAB del tetraedro está contenida en el plano OXY, y el vértice B es un punto del eje OY (ver figura). Utilizando las herramientas del Álgebra Vectorial, determina las coordenadas cartesianas de los vértices del tetraedro.
2.3 Volumen de un tetraedro
Halla el volumen de un tetraedro del cuál se sabe que las coordenadas
cartesianas de dos de sus vértices se corresponden con las ternas
A(0,1,1) y B(2, − 1,2), y que dos de las aristas que concurren en B
están definidas por los vectores libres 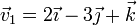 y
y
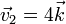 (las coordenadas están en metros).
(las coordenadas están en metros).
2.4 Distancia de un punto a un plano
Encuentra la ecuación del plano perpendicular al vector libre 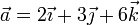 y que contiene a un punto P, cuya posición respecto del origen de un sistema de referencia OXYZ viene dada por el radio vector
y que contiene a un punto P, cuya posición respecto del origen de un sistema de referencia OXYZ viene dada por el radio vector 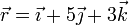 . Calcula la distancia que separa al origen O de dicho plano (todas las distancias están dadas en metros).
. Calcula la distancia que separa al origen O de dicho plano (todas las distancias están dadas en metros).
2.5 Distancia mínima entre dos rectas
Hallar la menor distancia entre las rectas Δ(A,B) y Γ(C,D), y determinar el vector (segmento orientado) de menor módulo que une ambas rectas. Las coordenadas cartesianas de los puntos que definen dichas rectas vienen dadas por las ternas A(1, − 2, − 1) y B(4,0, − 3), para el caso de Δ, y C(1,2, − 1) y D(2, − 4, − 5), para la recta Γ.
2.6 Condiciones sobre producto escalar y vectorial
Demuestra que si se cumplen simultáneamente las condiciones
siendo 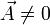 , entonces
, entonces 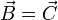 ;
pero si sólo se cumple una de ellas, entonces
;
pero si sólo se cumple una de ellas, entonces 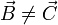 .
.
2.7 Derivada de un vector
Un punto recorre una circunferencia de radio R, de modo que en cada instante el vector que une el centro de la circunferencia con el punto forma un ángulo α con el eje OX.
- Encuentra la expresión del vector de posición del punto en función del ángulo α.
- Encuentra la expresión del vector de posición del punto en función del ángulo α.
- Si el ángulo α depende del tiempo como α = ωt, calcula la derivada del vector de posición respecto del tiempo.
2.8 Recta soporte de un vector deslizante
Un vector deslizante tiene como cursor el vector libre cursor 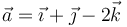 y su momento respecto al origen de coordenadas es
y su momento respecto al origen de coordenadas es 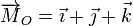 . Encuentra la ecuación vectorial de la recta soporte del vector deslizante.
. Encuentra la ecuación vectorial de la recta soporte del vector deslizante.