Ángulo capaz de 90 (G.I.A.)

De Laplace

1 Enunciado

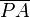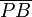Dada una circunferencia de centro $O$ y radio $R$ , y un diámetro $\overline{AB}$ cualquiera, demuestre que las cuerdas $\overline{PA}$ y $\overline{PB}$ se cortan perpendicularmente,para todo punto $P$ perteneciente a la circunferencia (arco capaz de $90 o$ ).

2 Solución

Siguiendo la figura podemos definir los vectores asociados a las cuerdas

$\begin{array}{c} \overrightarrow{AP} = \overrightarrow{AO} + \overrightarrow{OP}\\ \\ \overrightarrow{BP} = \overrightarrow{BO} + \overrightarrow{OP} \end{array}$

De la figura podemos observar que se cumple

$\begin{array}{l} \overrightarrow{AO}=-\overrightarrow{BO} \\ \\ |\overrightarrow{AO}| = |\overrightarrow{BO}| = R\\ \\ |\overrightarrow{OP}| = R \end{array}$

Calculamos el producto escalar de los vectores definidos por la cuerdas

$\begin{array}{ll} \overrightarrow{AP}\cdot\overrightarrow{BP}& = (\overrightarrow{AO}+\overrightarrow{OP})\cdot(\overrightarrow{BO}+\overrightarrow{OP})\\ &=\overrightarrow{AO}\cdot\overrightarrow{OP}+\overrightarrow{AO}\cdot\overrightarrow{BO}+ \overrightarrow{OP}\cdot\overrightarrow{OP}+\overrightarrow{OP}\cdot\overrightarrow{BO} \end{array}$

El primer y el último término se anulan pues $\overrightarrow{AO}=-\overrightarrow{BO}$ y el producto escalar es conmutativo. Queda entonces

$\overrightarrow{AP}\cdot\overrightarrow{BP}= \overrightarrow{AO}\cdot\overrightarrow{BO}+\overrightarrow{OP}\cdot\overrightarrow{OP}= -|\overrightarrow{AO}|^2 + |\overrightarrow{OP}|^2 = -R^2 + R^2 = 0.$

Con lo cual queda demostrado que las cuerdas son perpendiculares.

Ángulo capaz de 90 (G.I.A.)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES