Problemas de capacidad eléctrica (GIA)
De Laplace
(→Condensador plano de capacidad ajustable) |
(→Condensadores en asociación variable) |
||
| (35 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | __toc__ | ||
| + | |||
| + | ==[[Condensador plano paralelo (GIA)|Condensador plano paralelo]]== | ||
| + | Se tienen dos discos conductores idénticos, de radio <math>a=6\,\mathrm{cm}</math>, con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica <math>C_0\approx100\,\mathrm{pF}</math> | ||
| + | |||
| + | # Si los conductores están separados por aire, cuyo campo de ruptura es <math>E_\mathrm{air}=3\,\mathrm{kV/mm}</math>, ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos? | ||
| + | # Si se separan por una lámina de papel de espesor <math>\delta=0,1\,\mathrm{mm}</math>, cuya constante de dieléctrica es <math>\kappa\approx | ||
| + | 4</math>, y cuyo campo de ruptura es <math>E_\mathrm{pap}=12\,\mathrm{kV/mm}</math>, ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse? | ||
| + | |||
==[[Capacidad de un condensador cilíndrico GIA|Capacidad de un condensador cilíndrico]]== | ==[[Capacidad de un condensador cilíndrico GIA|Capacidad de un condensador cilíndrico]]== | ||
Calcular la capacidad de un condensador cilíndrico de radio interior <math>R_1</math>, radio exterior <math>R_2</math> y longitud <math>L</math> suponiendo que <math>R_1<R_2\ll L</math>. | Calcular la capacidad de un condensador cilíndrico de radio interior <math>R_1</math>, radio exterior <math>R_2</math> y longitud <math>L</math> suponiendo que <math>R_1<R_2\ll L</math>. | ||
| Línea 6: | Línea 15: | ||
<center>[[Archivo:cond_cilind.gif]]</center> | <center>[[Archivo:cond_cilind.gif]]</center> | ||
| - | ==[[ | + | ==[[Sistema de dos condensadores en paralelo (F2GIA) | Sistema de dos condensadores en paralelo]]== |
| + | Dos condensadores planos, ambos de la misma sección y con aire entre los planos, tienen capacidades eléctricas <math>C_1 = 6\,\mathrm{nF}\,</math> y <math>C_2 = 3\,\mathrm{nF}\,</math>. Los condensadores están conectados formando una asociación en paralelo, que se mantendrá en todo momento. La asociación descrita se conecta a una batería adquiriendo los condensadores una diferencia de potencial <math>\Delta V=6\,\mathrm{V}\,</math>. Después, se desconecta la asociación de la batería y se rellena todo el espacio existente entre las placas del segundo condensador (<math>C_2</math>) con un material de constante dieléctrica <math>\kappa</math> desconocida, y que soporta un campo eléctrico de <math>12\,\mathrm{kV/mm}</math> antes de la ruptura dieléctrica. | ||
| + | [[Archivo:cuest_condensadores_4.gif|right]] | ||
| + | #¿Cuál debe ser el valor de <math>\kappa</math> para que la nueva diferencia de potencial en los condensadores de la asociación sea <math>\Delta V' = 2\,\mathrm{V}\,</math>? | ||
| + | #Teniendo en cuenta que el aire sólo soporta un campo de <math>3\,\mathrm{kV/mm}\,</math>, calcular la relación entre la energía máxima que puede almacenar la asociación en paralelo de los dos condensadores en la situación final (cuando el segundo condensador está relleno del dieléctrico), y la energía máxima correspondiente a la situación inicial de los condensadores con aire. | ||
| - | Las armaduras de un condensador plano tienen una superficie <math>S=10\, \mathrm{cm}^2</math> y están separadas una distancia <math>a=2\,</math>mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A | + | ==[[Sistema_de_dos_condensadores_conectados,_F2_GIA_(Abr,_2013)|Sistema de dos condensadores conectados]]== |
| + | [[Archivo:sistema_condensadores_1.gif|right]]Dos condensadores de capacidades <math>C_1=3\,\mathrm{nF}</math> y <math>C_2=6\,\mathrm{nF}</math> están conectados formando inicialmente una asociación en serie. El conductor accesible del condensador <math>C_1</math>, que llamaremos “<math>\mathrm{C}_A</math>”, está conectado a un generador, que fija un valor de potencial de <math>V_A=10\,\mathrm{V}</math> en dicho conductor. El otro conductor accesible de la asociación, “<math>\mathrm{C}_B</math>” (correspondiente al condensador <math>C_2</math>), está conectado a una fuente de potencial de <math>V_B=5\,\mathrm{V}</math>. | ||
| + | |||
| + | # Las cantidades de carga <math>Q_A</math> y <math>Q_B</math> en los respectivos conductores “<math>\mathrm{C}_A</math>” y “<math>\mathrm{C}_B</math>”. | ||
| + | # Valor del potencial en el conductor ''flotante'' “<math>\mathrm{C}_\mathrm{f}</math>”, que en la asociación en serie permanece aislado y descargado. | ||
| + | # Manteniendo los conductores “<math>\mathrm{C}_A</math>” y “<math>\mathrm{C}_B</math>” conectados a las fuentes de potencial, se conecta el conductor flotante “<math>\mathrm{C}_\mathrm{f}</math>” a tierra, de manera que <math>V_\mathrm{f}=0\,\mathrm{V}</math>. ¿Qué cantidad total de carga eléctrica habrá ahora en dicho conductor? ¿Qué le ocurre a la energía almacenada en el sistema? | ||
| + | |||
| + | ==[[Condensador plano de capacidad ajustable GIA|Condensador plano de capacidad ajustable]]== | ||
| + | [[Archivo:cond_ajust.gif|right]]Las armaduras de un condensador plano tienen una superficie <math>S=10\, \mathrm{cm}^2</math> y están separadas una distancia <math>a=2\,</math>mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor <math>d=1\,</math>mm y de constante dieléctrica <math>\kappa=2</math> pegada a una de sus armaduras. Calcular: | ||
# Carga eléctrica en cada armadura del condensador. | # Carga eléctrica en cada armadura del condensador. | ||
# Capacidad del condensador con el dieléctrico. | # Capacidad del condensador con el dieléctrico. | ||
| - | # Distancia adicional que deben separarse las armaduras del | + | # Distancia adicional que deben separarse las armaduras del condensador después de introducir el dieléctrico para que su capacidad sea la misma que tenía antes de introducir el dieléctrico. |
| - | condensador después de introducir el dieléctrico para que su capacidad | + | |
| - | sea la misma que tenía antes de introducir el dieléctrico. | + | |
# Energía electrostática almacenada en el condensador relleno de aire, con la placa dieléctrica y después de separar las armaduras. | # Energía electrostática almacenada en el condensador relleno de aire, con la placa dieléctrica y después de separar las armaduras. | ||
| + | |||
| + | ==[[Energía_máxima_en_asociaciones_de_condensadores,_F2_GIA_(Abr,_2013)|Energía máxima en asociaciones de condensadores]]== | ||
| + | Se tienen dos condensadores idénticos, cada uno de ellos formado por dos discos conductores paralelos de sección <math>S</math>, separados por un medio dieléctrico de espesor <math>d</math>, constante dieléctrica <math>\kappa</math> y cuya ruptura dieléctrica se produce para un campo eléctrico de intensidad mayor o igual que un valor <math>E_\mathrm{rup}</math> conocido. ¿Cómo deben asociarse para poder almacenar el máximo de energía eléctrica en el sistema resultante de la | ||
| + | asociación? | ||
| + | |||
| + | ==[[Condensadores en asociación variable,_F2_GIA_(Sept,_2018)|Condensadores en asociación variable]]== | ||
| + | Se tienen tres condensadores de idéntica geometría, “1”, “2” y “3”, cuya capacidad eléctrica sería <math>C_0</math> si no hubiese ningún medio material dieléctrico separando los conductores. Sin embargo, están rellenos de sendos dieléctricos de constantes dieléctricas <math>\kappa_1</math>, <math>\kappa_2</math> y <math>\kappa_3</math>, respectivamente. Inicialmente se encuentran los tres descargados y los dos primeros están conectados en serie, con el conductor libre de “2” conectado al conductor de referencia o ''tierra''. Un generador electrostático de f.e.m. <math>V_0</math>, tiene su electrodo negativo conectado también al conductor de referencia. Se procede a conectar el electrodo positivo al conductor libre del condensador “1” para cargar la asociación en serie. Una vez realizado este paso, se desconecta el generador. Posteriormente, se conecta el conductor ''flotante'' de la asociación en serie formada por “1” y “2” a un conductor del condensador “3”, que tiene el otro conductor conectado a “tierra”. | ||
| + | |||
| + | [[Archivo:FII_gIA_18_19_bol_E3_7_0.png|right]] | ||
| + | |||
| + | # ¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de estos dos condensadores? ¿Cuál es el valor del potencial en el conductor ''flotante''? | ||
| + | # ¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador? | ||
| + | # Sean <math>\Delta V_1^\mathrm{max}</math>, <math>\Delta V_2^\mathrm{max}</math> y <math>\Delta V_3^\mathrm{max}</math> los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener <math>V_0</math>, en función de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que <math>\kappa_1<\kappa_2<\kappa_3</math> y <math>\Delta V_1^\mathrm{max}<\Delta | ||
| + | V_2^\mathrm{max}<\Delta V_3^\mathrm{max}</math>: ¿cuál debe ser el valor máximo de <math>V_0</math>? | ||
| + | |||
| + | ==[[Esfera_y_condensador_plano_paralelo,_F2_GIA_(Abr,_2014)|Esfera conectada a condensador plano paralelo]]== | ||
| + | |||
| + | El sistema de la figura está formado por una esfera conductora “C1” cuya capacidad eléctrica en el vacío es <math>C_e=10\,\mathrm{pF}</math>, y por dos discos conductores idénticos, “C2” y “C3”, ambos de radio <math>a=36\,\mathrm{mm}</math>, separados por una lámina de papel parafinado cuyos respectivos valores de constante dieléctrica y campo de ruptura son <math>\kappa=2.0</math> y <math>E_\mathrm{rup}^\kappa=30\,\mathrm{kV}/\mathrm{mm}</math>. Los discos y el papel forman un condensador plano paralelo relleno de dieléctrico, de capacidad <math>C_p=360\,\mathrm{pF}</math>. El disco conductor “C3” permanece en todo momento conectado ''a tierra'', por lo que el valor del potencial en todos los puntos de dicho disco es siempre <math>V_3=0\,\mathrm{V}</math>. El disco “C2” está conectado mediante un cable a la esfera “C1”, de manera que ambos conductores son siempre equipotenciales. Además, el cable es lo suficientemente largo y delgado como para que las distribuciones de carga en la esfera y el condensador no se vean mutuamente afectadas. | ||
| + | |||
| + | <center>[[Archivo:esfera_y_cpp_0.gif]]</center> | ||
| + | |||
| + | # La esfera “C1” se conecta al electrodo negativo de un generador ideal de fuerza electromotriz <math>V_0=300\,\mathrm{V}</math>, cuyo electrodo positivo está conectado a tierra. ¿Qué cantidad de carga <math>Q_i=Q\big\rfloor_{\mathrm{C}i}</math> se distribuye en cada uno de los conductores? | ||
| + | # En un determinado instante se desconecta la esfera “C1” del generador, pero manteniendo la conexión a tierra del disco “C3”. ¿Qué cantidad de energía eléctrica <math>U_e</math> se almacena en el sistema tras la desconexión? | ||
| + | # Tras desconectar la esfera del generador, se quiere retirar la lámina de papel parafinado del condensador, quedando éste relleno de aire. ¿Cómo cambian los valores de las magnitudes eléctricas en el sistema tras retirar la lámina de dieléctrico? | ||
| + | # ¿Qué condición debe verificar la fuerza electromotriz del generador, <math>V_0</math>, para que pueda retirarse la lámina dieléctrica sin que se produzca ruptura dieléctrica? (Campo de ruptura del aire: <math>E_\mathrm{rup}^0=3\,\mathrm{kV}/\mathrm{mm}</math>). | ||
| + | |||
| + | ==[[Asociación de cuatro condensadores GIA|Asociación de cuatro condensadores]]== | ||
| + | [[Archivo:cuatro_cond.gif|right]]El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: <math>C_1=1\,\mu\mathrm{F}</math>, <math>C_2=2\,\mu\mathrm{F}</math>, <math>C_3=3\,\mu\mathrm{F}</math> y <math>C_4=4\,\mu\mathrm{F}</math>. La diferencia de potencial entre A y B es de <math>12\,\mathrm{V}</math>. Calcular la carga de cada condensador. | ||
| + | |||
| + | | ||
| + | |||
| + | | ||
| + | |||
| + | | ||
| + | |||
| + | |||
| + | ==[[Sistema_electrostático_de_cuatro_discos_conductores,_F2_GIA_(Jun,_2013)|Sistema electrostático de cuatro discos conductores]]== | ||
| + | Un sistema de conductores está formado por cuatro discos metálicos idénticos, de sección <math>S</math>, colocados con sus respectivas superficies en planos paralelos y con sus centros en el mismo eje perpendicular a los discos. Las superficies enfrentadas de los dos discos centrales, “2” y “3”, están separadas una distancia <math>d/2</math>, mientras que sus otras superficies se mantienen a una distancia <math>d</math> de las de los discos “1” y “4”, colocados en los extremos del sistema. El valor de <math>d</math> es lo suficientemente pequeño frente al diámetro y grosor de los discos como para poder considerar que cada par de superficies conductoras enfrentadas se encuentran en influencia total, formando así un condensador plano paralelo relleno de aire. | ||
| + | |||
| + | [[Archivo:Sistema_cuatro_cond_0.gif|right]] | ||
| + | # Obtenga las expresiones para la carga eléctrica total en cada uno de los discos en función de los parámetros geométricos y de los valores del potencial electrostático en los discos. | ||
| + | # Los discos “1” y “3” se conectan mediante un cable conductor ideal, formando el conductor “A”, e igualmente se hace con “2” y “4” para forma el “B”. Justifique por qué los conductores surgidos de estas asociaciones forman un condensador y calcule su capacidad eléctrica equivalente. | ||
| + | # Considere el caso concreto en que el radio de los discos es de <math>R=36\,\mathrm{mm}</math> y la distancia <math>d=0.4\,\mathrm{mm}</math>. Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico <math>E_\mathrm{rup}^\mathrm{air}=3\,\mathrm{kV}/\mathrm{mm}</math>, determine la diferencia de potencial máxima, <math>V_\mathrm{max}</math>, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor <math>V_\mathrm{max}</math>? | ||
| + | # Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica <math>\kappa=7</math> y campo de ruptura <math>E_\mathrm{rup}^\mathrm{por}=5.7\,\mathrm{kV}/\mathrm{mm}</math>, ¿cuál será el valor de <math>V_\mathrm{max}</math> y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema? | ||
| + | |||
| + | ==[[Sistema_de_tres_discos_conductores,_F2_GIA_(Sept,_2012)|Sistema de tres discos conductores]]== | ||
| + | Se tiene un sistema formado por tres discos conductores de igual sección <math>S</math>, con sus superficies planas dispuestas en planos paralelos. El disco intermedio tiene un espesor <math>d/2</math> y está separado del disco inferior por una lámina de metacrilato de espesor <math>d</math>, cuya constante dieléctrica tiene un valor <math>\kappa\simeq 3</math>; una capa de aire de espesor <math>d/2</math> lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde. | ||
| + | |||
| + | # Determine las capacidades eléctricas de los dos condensadores formados por las superficies planas enfrentadas, en términos de los parámetros del sistema. | ||
| + | # Si se conectan los dos discos externos mediante un hilo conductor, ¿qué tipo de asociación de condensadores se forma? ¿Cuánto vale la capacidad eléctrica equivalente? | ||
| + | # En la situación del apartado anterior, determine la cantidad total de carga eléctrica en el conductor central cuando entre éste y los externos se establece una diferencia de potencial <math>V_0</math> mediante un generador electrostático. Determine también las cantidades de carga eléctrica en cada una de las superficies planas de los conductores. | ||
| + | # Tras desconectar el generador, dejando los discos aislados, se quita la lámina dieléctrica y, posteriormente, se desplaza el disco central de manera que sus superficies planas equidisten de los discos externos ¿Cúal será el valor <math>V^\prime</math> de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema. | ||
| + | # Sabiendo que los campos máximos de ruptura dieléctrica del aire y del metacrilato son de <math>\displaystyle 3</math> y <math>30\,kV/mm</math>, respectivamente, y considerando que <math>d = 1\,mm</math>, determine cuál es el valor máximo que puede tener <math>V_0</math> para que en ningún momento se produzca la ruptura dieléctrica. | ||
| + | |||
| + | <center>[[Archivo:p1_2acon_11_12_0.gif]]</center> | ||
| + | |||
[[Categoría:Problemas de capacidad eléctrica F2 GIA]] | [[Categoría:Problemas de capacidad eléctrica F2 GIA]] | ||
última version al 12:19 29 mar 2019
1 Condensador plano paralelo
Se tienen dos discos conductores idénticos, de radio 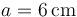 , con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica
, con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica 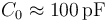
- Si los conductores están separados por aire, cuyo campo de ruptura es
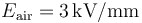 , ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
, ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
- Si se separan por una lámina de papel de espesor
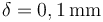 , cuya constante de dieléctrica es
, cuya constante de dieléctrica es 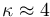 , y cuyo campo de ruptura es
, y cuyo campo de ruptura es 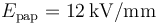 , ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?
, ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?
2 Capacidad de un condensador cilíndrico
Calcular la capacidad de un condensador cilíndrico de radio interior R1, radio exterior R2 y longitud L suponiendo que 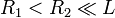 .
.
Si se sumerge parcialmente en líquido dieléctrico lineal, ¿cuál es su nueva capacidad? ¿Cómo cambia la energía acumulada en el condensador?
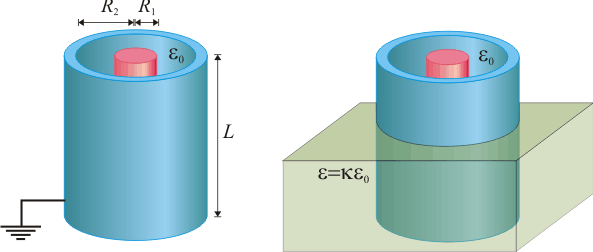
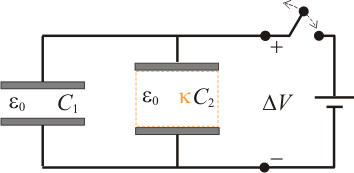
3 Sistema de dos condensadores en paralelo
Dos condensadores planos, ambos de la misma sección y con aire entre los planos, tienen capacidades eléctricas 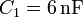 y
y 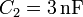 . Los condensadores están conectados formando una asociación en paralelo, que se mantendrá en todo momento. La asociación descrita se conecta a una batería adquiriendo los condensadores una diferencia de potencial
. Los condensadores están conectados formando una asociación en paralelo, que se mantendrá en todo momento. La asociación descrita se conecta a una batería adquiriendo los condensadores una diferencia de potencial 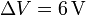 . Después, se desconecta la asociación de la batería y se rellena todo el espacio existente entre las placas del segundo condensador (C2) con un material de constante dieléctrica κ desconocida, y que soporta un campo eléctrico de
. Después, se desconecta la asociación de la batería y se rellena todo el espacio existente entre las placas del segundo condensador (C2) con un material de constante dieléctrica κ desconocida, y que soporta un campo eléctrico de 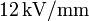 antes de la ruptura dieléctrica.
antes de la ruptura dieléctrica.
- ¿Cuál debe ser el valor de κ para que la nueva diferencia de potencial en los condensadores de la asociación sea
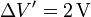 ?
?
- Teniendo en cuenta que el aire sólo soporta un campo de
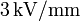 , calcular la relación entre la energía máxima que puede almacenar la asociación en paralelo de los dos condensadores en la situación final (cuando el segundo condensador está relleno del dieléctrico), y la energía máxima correspondiente a la situación inicial de los condensadores con aire.
, calcular la relación entre la energía máxima que puede almacenar la asociación en paralelo de los dos condensadores en la situación final (cuando el segundo condensador está relleno del dieléctrico), y la energía máxima correspondiente a la situación inicial de los condensadores con aire.
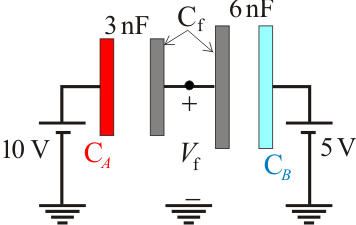
4 Sistema de dos condensadores conectados
Dos condensadores de capacidades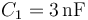 y
y 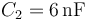 están conectados formando inicialmente una asociación en serie. El conductor accesible del condensador C1, que llamaremos “CA”, está conectado a un generador, que fija un valor de potencial de
están conectados formando inicialmente una asociación en serie. El conductor accesible del condensador C1, que llamaremos “CA”, está conectado a un generador, que fija un valor de potencial de 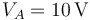 en dicho conductor. El otro conductor accesible de la asociación, “CB” (correspondiente al condensador C2), está conectado a una fuente de potencial de
en dicho conductor. El otro conductor accesible de la asociación, “CB” (correspondiente al condensador C2), está conectado a una fuente de potencial de 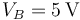 .
.
- Las cantidades de carga QA y QB en los respectivos conductores “CA” y “CB”.
- Valor del potencial en el conductor flotante “Cf”, que en la asociación en serie permanece aislado y descargado.
- Manteniendo los conductores “CA” y “CB” conectados a las fuentes de potencial, se conecta el conductor flotante “Cf” a tierra, de manera que
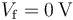 . ¿Qué cantidad total de carga eléctrica habrá ahora en dicho conductor? ¿Qué le ocurre a la energía almacenada en el sistema?
. ¿Qué cantidad total de carga eléctrica habrá ahora en dicho conductor? ¿Qué le ocurre a la energía almacenada en el sistema?
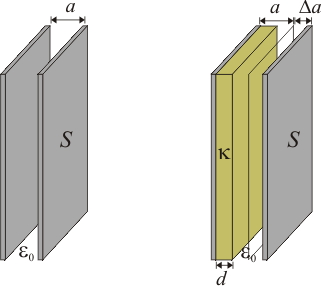
5 Condensador plano de capacidad ajustable
Las armaduras de un condensador plano tienen una superficie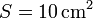 y están separadas una distancia
y están separadas una distancia 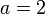 mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor
mm. El condensador se carga con una batería de 9 V y después se desconecta de la batería. A continuación se coloca una placa de material dieléctrico de espesor 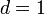 mm y de constante dieléctrica κ = 2 pegada a una de sus armaduras. Calcular:
mm y de constante dieléctrica κ = 2 pegada a una de sus armaduras. Calcular:
- Carga eléctrica en cada armadura del condensador.
- Capacidad del condensador con el dieléctrico.
- Distancia adicional que deben separarse las armaduras del condensador después de introducir el dieléctrico para que su capacidad sea la misma que tenía antes de introducir el dieléctrico.
- Energía electrostática almacenada en el condensador relleno de aire, con la placa dieléctrica y después de separar las armaduras.
6 Energía máxima en asociaciones de condensadores
Se tienen dos condensadores idénticos, cada uno de ellos formado por dos discos conductores paralelos de sección S, separados por un medio dieléctrico de espesor d, constante dieléctrica κ y cuya ruptura dieléctrica se produce para un campo eléctrico de intensidad mayor o igual que un valor Erup conocido. ¿Cómo deben asociarse para poder almacenar el máximo de energía eléctrica en el sistema resultante de la asociación?
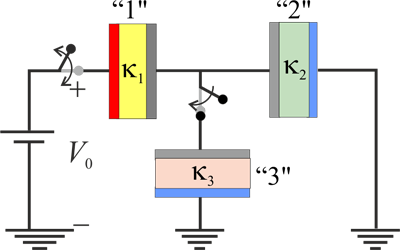
7 Condensadores en asociación variable
Se tienen tres condensadores de idéntica geometría, “1”, “2” y “3”, cuya capacidad eléctrica sería C0 si no hubiese ningún medio material dieléctrico separando los conductores. Sin embargo, están rellenos de sendos dieléctricos de constantes dieléctricas κ1, κ2 y κ3, respectivamente. Inicialmente se encuentran los tres descargados y los dos primeros están conectados en serie, con el conductor libre de “2” conectado al conductor de referencia o tierra. Un generador electrostático de f.e.m. V0, tiene su electrodo negativo conectado también al conductor de referencia. Se procede a conectar el electrodo positivo al conductor libre del condensador “1” para cargar la asociación en serie. Una vez realizado este paso, se desconecta el generador. Posteriormente, se conecta el conductor flotante de la asociación en serie formada por “1” y “2” a un conductor del condensador “3”, que tiene el otro conductor conectado a “tierra”.
- ¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de estos dos condensadores? ¿Cuál es el valor del potencial en el conductor flotante?
- ¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador?
- Sean
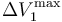 ,
, 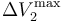 y
y 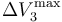 los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener V0, en función de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que κ1 < κ2 < κ3 y
los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener V0, en función de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que κ1 < κ2 < κ3 y 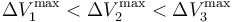 : ¿cuál debe ser el valor máximo de V0?
: ¿cuál debe ser el valor máximo de V0?
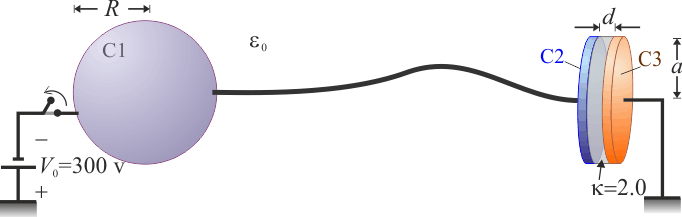
8 Esfera conectada a condensador plano paralelo
El sistema de la figura está formado por una esfera conductora “C1” cuya capacidad eléctrica en el vacío es 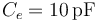 , y por dos discos conductores idénticos, “C2” y “C3”, ambos de radio
, y por dos discos conductores idénticos, “C2” y “C3”, ambos de radio 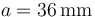 , separados por una lámina de papel parafinado cuyos respectivos valores de constante dieléctrica y campo de ruptura son κ = 2.0 y
, separados por una lámina de papel parafinado cuyos respectivos valores de constante dieléctrica y campo de ruptura son κ = 2.0 y 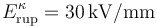 . Los discos y el papel forman un condensador plano paralelo relleno de dieléctrico, de capacidad
. Los discos y el papel forman un condensador plano paralelo relleno de dieléctrico, de capacidad 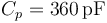 . El disco conductor “C3” permanece en todo momento conectado a tierra, por lo que el valor del potencial en todos los puntos de dicho disco es siempre
. El disco conductor “C3” permanece en todo momento conectado a tierra, por lo que el valor del potencial en todos los puntos de dicho disco es siempre 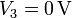 . El disco “C2” está conectado mediante un cable a la esfera “C1”, de manera que ambos conductores son siempre equipotenciales. Además, el cable es lo suficientemente largo y delgado como para que las distribuciones de carga en la esfera y el condensador no se vean mutuamente afectadas.
. El disco “C2” está conectado mediante un cable a la esfera “C1”, de manera que ambos conductores son siempre equipotenciales. Además, el cable es lo suficientemente largo y delgado como para que las distribuciones de carga en la esfera y el condensador no se vean mutuamente afectadas.
- La esfera “C1” se conecta al electrodo negativo de un generador ideal de fuerza electromotriz
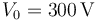 , cuyo electrodo positivo está conectado a tierra. ¿Qué cantidad de carga
, cuyo electrodo positivo está conectado a tierra. ¿Qué cantidad de carga 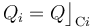 se distribuye en cada uno de los conductores?
se distribuye en cada uno de los conductores?
- En un determinado instante se desconecta la esfera “C1” del generador, pero manteniendo la conexión a tierra del disco “C3”. ¿Qué cantidad de energía eléctrica Ue se almacena en el sistema tras la desconexión?
- Tras desconectar la esfera del generador, se quiere retirar la lámina de papel parafinado del condensador, quedando éste relleno de aire. ¿Cómo cambian los valores de las magnitudes eléctricas en el sistema tras retirar la lámina de dieléctrico?
- ¿Qué condición debe verificar la fuerza electromotriz del generador, V0, para que pueda retirarse la lámina dieléctrica sin que se produzca ruptura dieléctrica? (Campo de ruptura del aire:
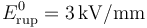 ).
).
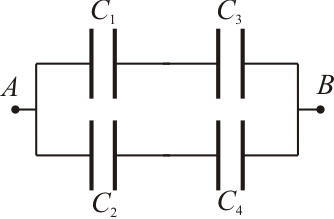
9 Asociación de cuatro condensadores
El circuito de la figura está formado por cuatro condensadores cuyas capacidades son: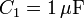 ,
, 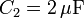 ,
, 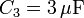 y
y 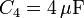 . La diferencia de potencial entre A y B es de
. La diferencia de potencial entre A y B es de 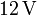 . Calcular la carga de cada condensador.
. Calcular la carga de cada condensador.
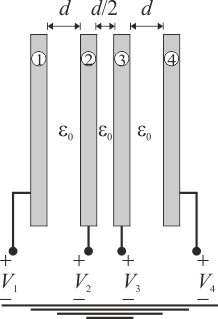
10 Sistema electrostático de cuatro discos conductores
Un sistema de conductores está formado por cuatro discos metálicos idénticos, de sección S, colocados con sus respectivas superficies en planos paralelos y con sus centros en el mismo eje perpendicular a los discos. Las superficies enfrentadas de los dos discos centrales, “2” y “3”, están separadas una distancia d / 2, mientras que sus otras superficies se mantienen a una distancia d de las de los discos “1” y “4”, colocados en los extremos del sistema. El valor de d es lo suficientemente pequeño frente al diámetro y grosor de los discos como para poder considerar que cada par de superficies conductoras enfrentadas se encuentran en influencia total, formando así un condensador plano paralelo relleno de aire.
- Obtenga las expresiones para la carga eléctrica total en cada uno de los discos en función de los parámetros geométricos y de los valores del potencial electrostático en los discos.
- Los discos “1” y “3” se conectan mediante un cable conductor ideal, formando el conductor “A”, e igualmente se hace con “2” y “4” para forma el “B”. Justifique por qué los conductores surgidos de estas asociaciones forman un condensador y calcule su capacidad eléctrica equivalente.
- Considere el caso concreto en que el radio de los discos es de
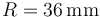 y la distancia
y la distancia 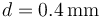 . Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico
. Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico 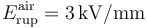 , determine la diferencia de potencial máxima, Vmax, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor Vmax?
, determine la diferencia de potencial máxima, Vmax, que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor Vmax?
- Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica κ = 7 y campo de ruptura
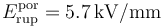 , ¿cuál será el valor de Vmax y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema?
, ¿cuál será el valor de Vmax y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema?
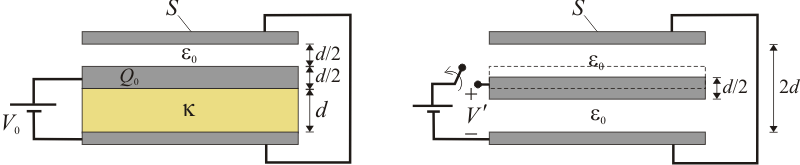
11 Sistema de tres discos conductores
Se tiene un sistema formado por tres discos conductores de igual sección S, con sus superficies planas dispuestas en planos paralelos. El disco intermedio tiene un espesor d / 2 y está separado del disco inferior por una lámina de metacrilato de espesor d, cuya constante dieléctrica tiene un valor 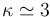 ; una capa de aire de espesor d / 2 lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde.
; una capa de aire de espesor d / 2 lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde.
- Determine las capacidades eléctricas de los dos condensadores formados por las superficies planas enfrentadas, en términos de los parámetros del sistema.
- Si se conectan los dos discos externos mediante un hilo conductor, ¿qué tipo de asociación de condensadores se forma? ¿Cuánto vale la capacidad eléctrica equivalente?
- En la situación del apartado anterior, determine la cantidad total de carga eléctrica en el conductor central cuando entre éste y los externos se establece una diferencia de potencial V0 mediante un generador electrostático. Determine también las cantidades de carga eléctrica en cada una de las superficies planas de los conductores.
- Tras desconectar el generador, dejando los discos aislados, se quita la lámina dieléctrica y, posteriormente, se desplaza el disco central de manera que sus superficies planas equidisten de los discos externos ¿Cúal será el valor
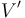 de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema.
de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema.
- Sabiendo que los campos máximos de ruptura dieléctrica del aire y del metacrilato son de
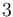 y
y 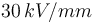 , respectivamente, y considerando que
, respectivamente, y considerando que 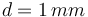 , determine cuál es el valor máximo que puede tener V0 para que en ningún momento se produzca la ruptura dieléctrica.
, determine cuál es el valor máximo que puede tener V0 para que en ningún momento se produzca la ruptura dieléctrica.