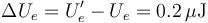Entrar Página Discusión Historial Go to the site toolbox

Sistema de dos condensadores conectados, F2 GIA (Abr, 2013)

De Laplace

Contenido

1 Enunciado

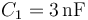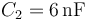Dos condensadores de capacidades C_1=3\,\mathrm{nF} y C_2=6\,\mathrm{nF} están conectados formando inicialmente una asociación en serie. El conductor accesible del condensador C1, que llamaremos “CA”, está conectado a un generador, que fija un valor de potencial de 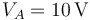V_A=10\,\mathrm{V} en dicho conductor. 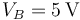El otro conductor accesible de la asociación, “CB” (correspondiente al condensador C2), está conectado a una fuente de potencial de V_B=5\,\mathrm{V}.
  1. Las cantidades de carga QA y QB en los respectivos conductores “CA” y “CB”.
  2. Valor del potencial en el conductor flotante “Cf”, que en la asociación en serie permanece aislado y descargado.
  3. Manteniendo los conductores “CA” y “CB” conectados a las fuentes de potencial, se conecta el conductor flotante “Cf” a tierra, de manera que 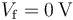V_\mathrm{f}=0\,\mathrm{V}. ¿Qué cantidad total de carga eléctrica habrá ahora en dicho conductor? ¿Qué le ocurre a la energía almacenada en el sistema?

2 Solución

2.1 Carga eléctrica en los conductores

En cada uno de los condensadores del sistema, las correspondientes parejas de conductores que los forman se hallan en influencia total. De esta forma, en el conductor “CA” y en la superficie conductora del “Cf” que se haya en influencia total con aquél, habrá cantidades opuestas de carga + QA y − QA, respectivamente. Análogamente, en el conductor “CB” y en la superficie conductora del conductor “Cf” enfrentada a aquél, habrá sendas cantidades de carga + QB y − QB. Por otra parte, el conductor flotante “Cf” se encuentra aislado y descargado (carga total nual en todo instantes), de manera que: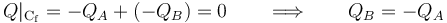
Q|_{\mathrm{C}_\mathrm{f}}=-Q_A+(-Q_B)=0\qquad\Longrightarrow\qquad Q_B=-Q_A

Es decir, los conductores de “CA” y “CB” tienen cantidades opuestas, por lo que la asociación de los dos condensadores conectados es equivalente a un único condensador, de capacidad Cser, tal que:

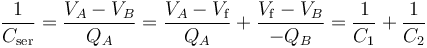
\frac{1}{C_\mathrm{ser}}=\frac{V_A-V_B}{Q_A}=\frac{V_A-V_\mathrm{f}}{Q_A}+\frac{V_\mathrm{f}-V_B}{-Q_B}=\frac{1}{C_1}+\frac{1}{C_2}

Como sabemos, este tipo de asociación se denomina en serie. Con los valores de capacidad de los condensadores del sistema, se obtiene que la capacidad del condensandor equivalente es:

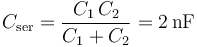
C_\mathrm{ser}=\frac{C_1\!\ C_2}{C_1+C_2}=2\,\mathrm{nF}

Y aplicando las relaciones anteriores y teniendo en cuenta los valores de diferencia de potencial fijados por las fuentes en los conductores “CA” y “CB”, se obtiene:

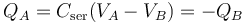
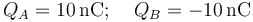
\displaystyle Q_A=C_\mathrm{ser}(V_A-V_B)=-Q_B       \Rightarrow       Q_A=10\,\mathrm{nC}\mathrm{;}\quad\;Q_B=-10\,\mathrm{nC}\,

2.2 Potencial del conductor flotante

Para determinar el valor del potencial Vf al que se halla el conductor flotante “Cf” consideremos por separado cualquiera de los condensadores de la asociación. Por ejemplo:

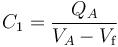
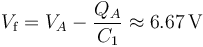
C_1=\frac{Q_A}{V_A-V_\mathrm{f}}       \Rightarrow       V_\mathrm{f}=V_A-\frac{Q_A}{C_1}\approx 6.67\,\mathrm{V}\,

Si hubiésemos utilizado el otro condensador...

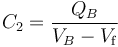
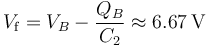
C_2=\frac{Q_B}{V_B-V_\mathrm{f}}       \Rightarrow       V_\mathrm{f}=V_B-\frac{Q_B}{C_2}\approx 6.67\,\mathrm{V}\,

2.2.1 Energía electrostática almacenada

Una vez determinadas las cantides de carga eléctrica en los conductores del sistema y los valores de potencial a que se éstos se encuentran, el cálculo de la energía electrostática en el sistema es inmediato:

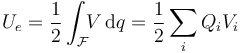
U_e=\frac{1}{2}\int_\mathcal{F}\!\! V\!\ \mathrm{d}q=\frac{1}{2}\sum_iQ_iV_i       \Rightarrow       U_e=\frac{1}{2}\bigg[Q_AV_A-\overbrace{(Q_A+Q_B)}^{=0}V_\mathrm{f}+Q_BV_B\bigg]=25\,\mathrm{nJ}\,

2.3 Conexión a tierra del conductor inicialmente asilado aislado

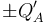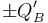Al conectar a tierra el conductor inicialmente aislado “Cf”, se deshace la asociación en serie. Ahora el sistema está formado por dos condensadores de capacidades C1 y C2 en los que se fijan respectivas diferencias de potencial VA y VB, mediante sendas fuentes. Las cargas \pm Q^\prime_A y \pm Q^\prime_B que se distribuyen en los condcutores en influencia total de los respectivos condesandores deben ser tales que:
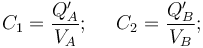
C_1=\frac{Q_A^\prime}{V_A}\mathrm{;}\quad\;\;C_2=\frac{Q_B^\prime}{V_B}\mathrm{;}

Y como los valores del potencial de las fuentes y de la capacidad eléctrica de los condesandores son independientes, también lo serán las cantidades de carga distribuidas en los conductores. Sin embargo, puesto que los conductores que están conectados “a tierra” siguen conectados entre sí, formando un único conductor “Cf”, la carga total que hay en dicho conductor es:

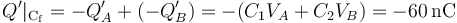
Q^\prime|_{\mathrm{C}_\mathrm{f}}=-Q^\prime_A+(-Q_B^\prime)=-(C_1V_A+C_2V_B)=-60\,\mathrm{nC}\,

2.3.1 Cambios en la energía electrostática almacenada

La energía electrostática almacenada en esta nueva configuración es:

U_e^\prime=\frac{1}{2}\sum_iQ_i^\prime V_i^\prime=\frac{1}{2}\bigg[Q_A^\prime V_A-(Q_A^\prime+Q_B^\prime)\overbrace{V_\mathrm{f}}^{=0}+Q_B^\prime V_B\bigg]       \Rightarrow       U_e^\prime=\frac{1}{2}\bigg[C_1V_A^2+C_2V_B^2\bigg]=225\,\mathrm{nJ}\,

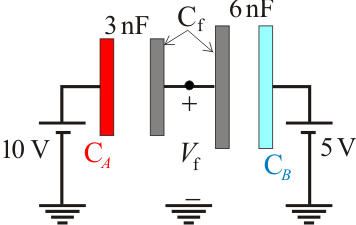
En consecuencia, al conectar el conductor “Cf” a tierra , la energía electrostática del sistema aumenta; concretamente:

\Delta U_e=U_e^\prime-U_e=0.2\,\mu\mathrm{J}\,
Obtenido de "http://tesla.us.es/wiki/index.php/Sistema_de_dos_condensadores_conectados,_F2_GIA_(Abr,_2013)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 12:17, 27 mar 2014. - Esta página ha sido visitada 4.761 veces. - Aviso legal - Acerca de Laplace