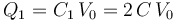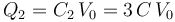Sistema de tres discos conductores, F2 GIA (Sept, 2012)

De Laplace

1 Enunciado

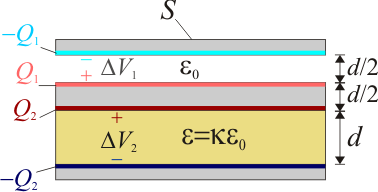
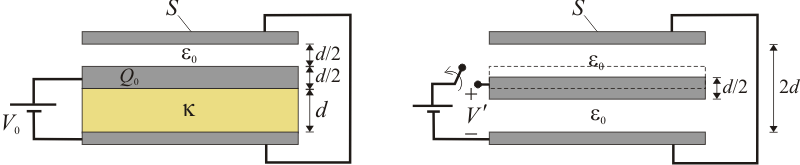
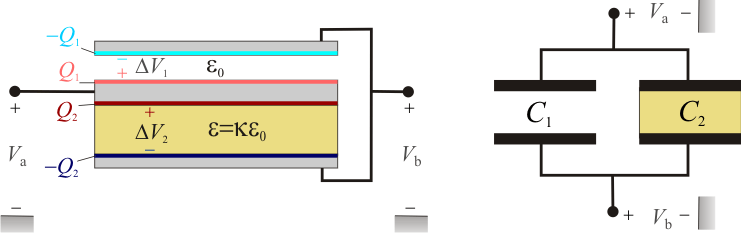
Se tiene un sistema formado por tres discos conductores de igual sección S, con sus superficies planas dispuestas en planos paralelos. El disco intermedio tiene un espesor d / 2 y está separado del disco inferior por una lámina de metacrilato de espesor d, cuya constante dieléctrica tiene un valor 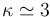; una capa de aire de espesor d / 2 lo separa del disco superior. El radio de los discos es considerablemente mayor que las distancias que los separan, de manera que podrán despreciarse los efectos de borde.

1. Determine las capacidades eléctricas de los dos condensadores formados por las superficies planas enfrentadas, en términos de los parámetros del sistema.
2. Si se conectan los dos discos externos mediante un hilo conductor, ¿qué tipo de asociación de condensadores se forma? ¿Cuánto vale la capacidad eléctrica equivalente?
3. En la situación del apartado anterior, determine la cantidad total de carga eléctrica en el conductor central cuando entre éste y los externos se establece una diferencia de potencial V₀ mediante un generador electrostático. Determine también las cantidades de carga eléctrica en cada una de las superficies planas de los conductores.
4. Tras desconectar el generador, dejando los discos aislados, se quita la lámina dieléctrica y, posteriormente, se desplaza el disco central de manera que sus superficies planas equidisten de los discos externos ¿Cúal será el valor 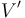de la diferencia de potencial entre los discos? Determine también la variación experimentada por la energía electrostática almacenada en el sistema.
5. Sabiendo que los campos máximos de ruptura dieléctrica del aire y del metacrilato son de 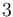y 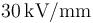, respectivamente, y considerando que , determine cuál es el valor máximo que puede tener V₀ para que en ningún momento se produzca la ruptura dieléctrica.

2 Solución

2.1 Capacidad eléctrica de los condensadores

Asumimos que los diámetros de los discos son lo suficientemente grandes frente a las distancias que separan las placas para que las superficies conductoras se encuentren en influencia total, formando sendos condensadores plano-paralelos. Además, consideraremos que estas mismas características geométricas permiten despreciar los efectos de la acumulación de carga en los bordes de los conductores sobre la capacidad eléctrica de los condesadores. Por tanto, se tendrá:

      

      

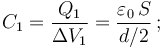
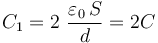
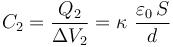
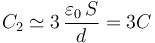
2.2 Asociación y capacidad equivalente

Si se conectan los discos exteriores mediante un cable conductor, aquéllos estarán al mismo valor V_b de potencial electrostático y, por tanto, las caras internas de dichos discos son equipotenciales. En consecuencia, si el disco interior se encuentra a un valor de potencial V_a, las diferencias de potencial ΔV₁ y ΔV₂ existentes entre superficies que se encuentran en influencia total, formando los respectivos condesadores C₁ y C₂, estarán serán iguales:

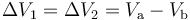
Es decir, dichos condensadores están asociados en paralelo, de forma que la capacidad equivalente de la asociación será:

      

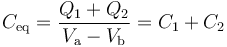
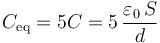
2.3 Carga eléctrica en los conductores

Se procede a conectar un generador electrostático que establece una diferencia de potencial fija V₀ entre el disco interior y los discos exteriores equipotenciales. La cantidad total de carga Q₀ que de almacena en el disco interior será igual a la suma de las que haya en cada una de sus caras, de manera que:

      

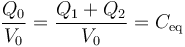
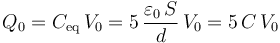
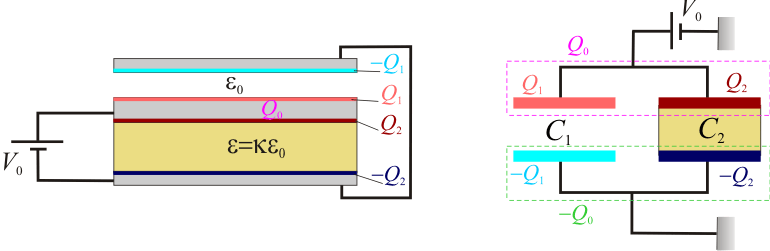
Las cantidades parciales de carga Q₁ y Q₂ que se almacenan en cada una de las caras del conductor central también estarán determinadas por la diferencia de potencial V₀ existente entre las superficies en influencia total de ambos condensadores: