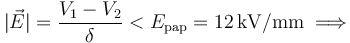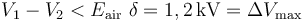Condensador plano paralelo (GIA)
De Laplace
Contenido |
1 Enunciado
Se tienen dos discos conductores idénticos, de radio 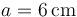 , con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica
, con los que se quiere construir un condensador plano-paralelo de capacidad eléctrica 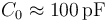
- Si los conductores están separados por aire, cuyo campo de ruptura es
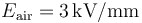 , ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
, ¿qué distancia debe existir entre los discos conductores? ¿Cuál es el máximo valor de diferencia de potencial que puede aplicarse entre los discos?
- Si se separan por una lámina de papel de espesor
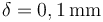 , cuya constante de dieléctrica es
, cuya constante de dieléctrica es 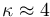 , y cuyo campo de ruptura es
, y cuyo campo de ruptura es 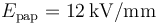 , ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?
, ¿cuál será la capacidad eléctrica y la diferencia de potencial que puede aplicarse?
2 Introducción
- El condensador plano-paralelo
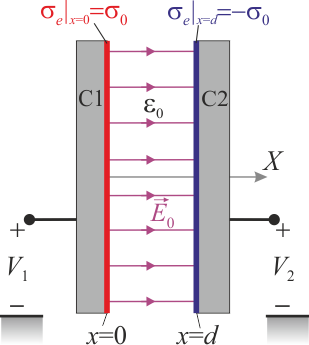
Un condensador plano paralelo es un sistema formado por dos superficies conductoras planas iguales, enfrentadas y dispuestas en sendos planos paralelos, separadas por un medio dieléctrico. Además, ambas superficies conductoras se están en influencia total: soportan cantidades opuestas de carga eléctrica y, por tanto, todas las líneas del campo eléctrico que “salen” del plano con carga positiva + Q, “terminan” en el plano con la carga negativa − Q.
Adoptaremos un sistema de referencia tal que los planos conductores enfrentados y cargados, coindicen con los planos geométricos 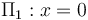 y
y 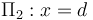 , ambos perpendiculares al eje OX. Además, consideraremos que el dieléctrio que separa ambos planos es el vacío, cuya permitividad dieléctica en el Sistema Internacional de unidades es
, ambos perpendiculares al eje OX. Además, consideraremos que el dieléctrio que separa ambos planos es el vacío, cuya permitividad dieléctica en el Sistema Internacional de unidades es 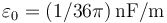 .
.
En un condensador real con conductores de tamaño finito y planos en influencia total de área S, las cargas eléctricas se ditribuyen más o menos uniformemente en puntos alejados de los bordes de los planos conductores; los valores absolutos de las densidades de carga eléctrica crecen conforme nos aproximamos a dichos bordes. Sin embargo, si la distancia 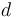 que separa los planos conductores es significativamente menor que las dimensiones de dichos planos, es posible despreciar estos efectos de borde y considerar, en primera aproximación, que las cargas eléctricas se distribuyen prácticamente de manera uniforme en los planos conductores, estando descritas por sendas densidades superficiales de carga constantes y opuestas:
que separa los planos conductores es significativamente menor que las dimensiones de dichos planos, es posible despreciar estos efectos de borde y considerar, en primera aproximación, que las cargas eléctricas se distribuyen prácticamente de manera uniforme en los planos conductores, estando descritas por sendas densidades superficiales de carga constantes y opuestas:
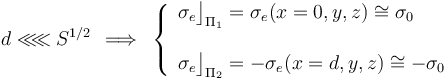
En consecuencia, las cantidades opuestas de carga distribuidas en los planos conductores serán:

Como pudo comprobarse en el ejercicio dedicado al estudio del campo eléctrico creado por planos cargados uniformemente, dos distribuciones superficiales de carga constantes y opuestas, localizadas en dos planos paralelos enfrentados separadas por vacío, sólo crean campo eléctrico en los puntos situados entre los planos. Y éste es uniforme, perpendicular a los planos cargados y de módulo proporcional al valor absoluto de la densidad constante de carga. En el caso que nos ocupa, se tendrá que...
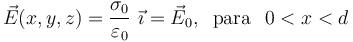
Este campo eléctrico implica la existencia de un potencial electrostático 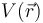 , en el que las superficies conductoras son superficies equipotenciales. La diferencia de potencial entre ambas es igual a la circulación del campo entre sendos puntos de dichos conductores. Si se calcula a lo largo de una línea cuyos puntos estén todos situados entre los planos
, en el que las superficies conductoras son superficies equipotenciales. La diferencia de potencial entre ambas es igual a la circulación del campo entre sendos puntos de dichos conductores. Si se calcula a lo largo de una línea cuyos puntos estén todos situados entre los planos 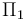 y
y 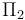 , se tendrá:
, se tendrá:
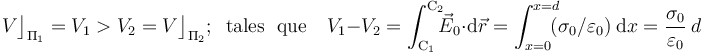
- Capacidad eléctrica del condensador plano paralelo
Las propiedades eléctricas y el comportamiento de un condensador en un circuito están caracterizadas por su capacidad eléctrica C, definida como la relación entre la carga eléctrica que se distribuye en uno de sus conductores y la diferencia de potencial entre éste y el otro conductor. Se trata de un parámetro que depende de la geometría del sistema(forma de los conductores, posición relativa,...) y del medio dieléctrico que se interpone entre los conductores. En el caso del condensador plano paralelo analizado, con espacio vacío entre los conductores, la capacidad eléctrica 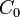 será:
será:

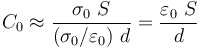
Hay que insistir en que anterior expresión se ha obtenido considerando despreciables o no significativos los efectos de acumulación de carga en los bordes de los conductores; es decir, en el caso de un condensador plano paralelo real el resultado anterior no es rigurosamente exacto, pero proporciona un valor de la capacidad eléctrica tanto más preciso, cuanto menor sea la distancia de separación entre los planos, en relación con las dimensiones de éstos.
Si entre los conductores de un condensador se coloca un conductor lineal homogéneo, la capacidad del condensador se multiplica por un factor κ (constante dieléctrica), que depende exclusivamente del material. En el caso del condensador plano paralelo, relleno de dieléctrico lineal...
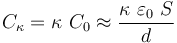
- Campo de ruptura del dieléctrico
En el caso del condensador relleno de un material dieléctrico lineal, existe otro importante parámetro de diseño: el campo de ruptura dieléctrica. Es decir, el valor máximo que puede tener la intensidad del campo eléctrico en el interior del medio dielétrico sin que se produzca la ionización de las moléculas o átomos que lo componen. El valor de este campo de ruptura es una característica de cada material, y va a condicionar cuál es la máxima diferencia de potencial que puede existir entre los conductores. En el caso del condensador plano paralelo relleno de dieléctrico lineal, el campo eléctrico en el interior también es uniforme. Por tanto...
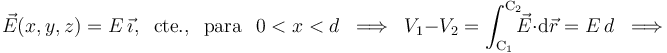
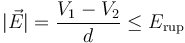
3 Solución
3.1 Condensador plano relleno de aire
Se tienen dos discos conductores de radio 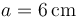 , con los que se quiere construir un condensador relleno de aire cuya capacidad eléctrica sea de
, con los que se quiere construir un condensador relleno de aire cuya capacidad eléctrica sea de 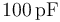 , aproximadamente. Se trataría de un condensador plano paralelo con los planos de los discos conductores en influencia. Si el dieléctrico que separa los discos conductores es aire, la capacidad eléctrica de este condensador será:
, aproximadamente. Se trataría de un condensador plano paralelo con los planos de los discos conductores en influencia. Si el dieléctrico que separa los discos conductores es aire, la capacidad eléctrica de este condensador será:
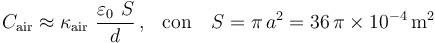
siendo d la distancia de separación entre los planos. La constante dieléctrica del aire es  . Es decir, la capacidad eléctrica de un condensador es prácticamente la misma en vacío que relleno de aire. Por tanto, para que la capacidad el condensador sea la requerida, la distancia de separación deberá ser:
. Es decir, la capacidad eléctrica de un condensador es prácticamente la misma en vacío que relleno de aire. Por tanto, para que la capacidad el condensador sea la requerida, la distancia de separación deberá ser:
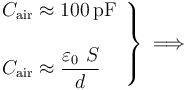
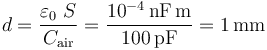
Se comprueba que las dimensiones de los discos (sus diámetros), son considerablemente mayores que la distancia de separación,

por lo que es de esperar que la expresión utilizada para la capacidad eléctrica del condensador, proporciona valores adecuados de esta magnitud.
Para determinar cuál es la máxima diferencia de potencial que se puede aplicar entre los conductores de este condensador, imponemos la condición de que la intensidad del campo eléctrico uniforme que exista dentro del condensador, no puede superar el campo de ruptura del aire:
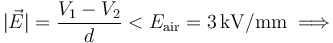
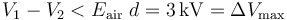
3.2 Condensador plano relleno de dieléctrico (lámina de papel)
Se separan los discos conductores mediante una lámina de papel de espesor 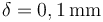 , cuya constante dieléctrica es
, cuya constante dieléctrica es 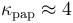 . En estas condiciones, la capacidad del condensador plano paralelo será:
. En estas condiciones, la capacidad del condensador plano paralelo será:
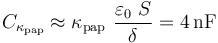
Para determinar ahora la diferencia de potecial máxima que puede establecerse entre los conductores, se ha de tener en cuenta que han cambiado tanto el campo de ruptura como la distancia de separación: