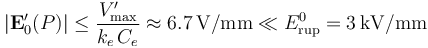Esfera y condensador plano paralelo, F2 GIA (Abr, 2014)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

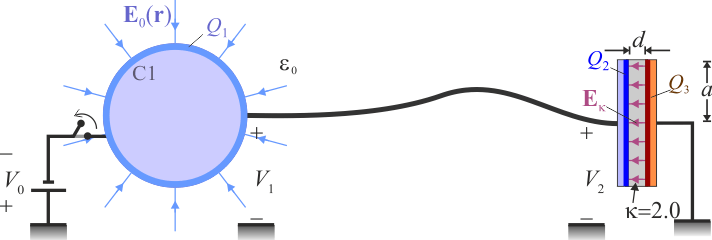
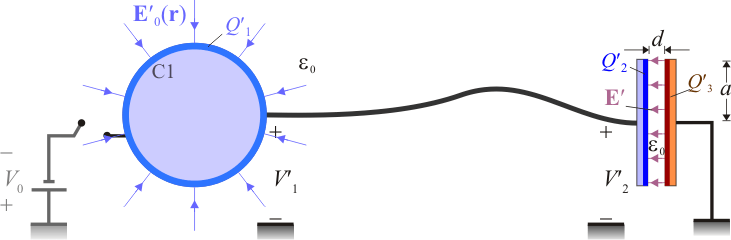
El sistema de la figura está formado por una esfera conductora “C1” cuya capacidad eléctrica en el vacío es 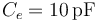$C_e=10\,\mathrm{pF}$ , y por dos discos conductores idénticos, “C2” y “C3”, ambos de radio 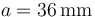$a=36\,\mathrm{mm}$ , separados por una lámina de papel parafinado cuyos respectivos valores de constante dieléctrica y campo de ruptura son $κ = 2.0$ y 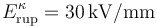$E_\mathrm{rup}^\kappa=30\,\mathrm{kV}/\mathrm{mm}$ . Los discos y el papel forman un condensador plano paralelo relleno de dieléctrico, de capacidad 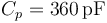$C_p=360\,\mathrm{pF}$ . El disco conductor “C3” permanece en todo momento conectado a tierra, por lo que el valor del potencial en todos los puntos de dicho disco es siempre 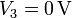$V_3=0\,\mathrm{V}$ . El disco “C2” está conectado mediante un cable a la esfera “C1”, de manera que ambos conductores son siempre equipotenciales. Además, el cable es lo suficientemente largo y delgado como para que las distribuciones de carga en la esfera y el condensador no se vean mutuamente afectadas.

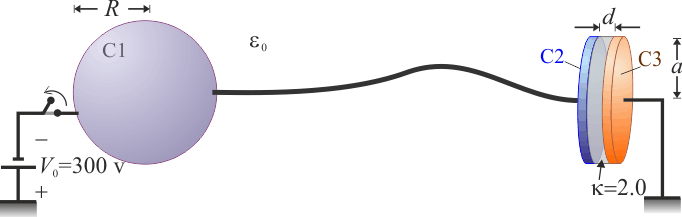
La esfera “C1” se conecta al electrodo negativo de un generador ideal de fuerza electromotriz 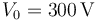$V_0=300\,\mathrm{V}$ , cuyo electrodo positivo está conectado a tierra. ¿Qué cantidad de carga 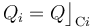$Q_i=Q\big\rfloor_{\mathrm{C}i}$ se distribuye en cada uno de los conductores?
En un determinado instante se desconecta la esfera “C1” del generador, pero manteniendo la conexión a tierra del disco “C3”. ¿Qué cantidad de energía eléctrica $U e$ se almacena en el sistema tras la desconexión?
Tras desconectar la esfera del generador, se quiere retirar la lámina de papel parafinado del condensador, quedando éste relleno de aire. ¿Cómo cambian los valores de las magnitudes eléctricas en el sistema tras retirar la lámina de dieléctrico?
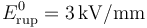¿Qué condición debe verificar la fuerza electromotriz del generador, $V 0$ , para que pueda retirarse la lámina dieléctrica sin que se produzca ruptura dieléctrica? (Campo de ruptura del aire: $E_\mathrm{rup}^0=3\,\mathrm{kV}/\mathrm{mm}$ ).

2 Solución

2.1 Carga eléctrica en los conductores

Las cantidades de carga eléctrica en los diferentes conductores del sistema estarán determinadas por las capacidades eléctricas de la esfera y del condensador plano paralelo que forman los dos discos, y por el valor del potencial eléctrostático, 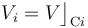$V_i=V\big\rfloor_{\mathrm{C}i}$ en cada uno de ellos. El disco “C3” se encuentra a potencial nulo en todo momento, mientras que el valor del potencial de la esfera “C1” y el disco “C2” estará fijado por estar conectados al electrodo negativo del generador:

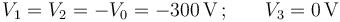
$V_1=V_2=-V_0=-300\,\mathrm{V}\!\ \mathrm{;}\qquad V_3=0\,\mathrm{V}$

Como el cable que une los conductores “C1” y “C2” es lo suficientemente largo como para que las cargas eléctricas en estos conductores no se afecten mutuamente, podemos considerar que la carga en el conductor esférico se distribuye uniformemente en su superficie, de manera que:

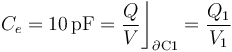
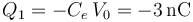
$C_e=10\,\mathrm{pF}=\frac{Q}{V}\bigg\rfloor_{\partial\mathrm{C1}}=\frac{Q_1}{V_1}$ $\Rightarrow$ $Q_1=-C_e\!\ V_0=-3\,\mathrm{nC}$

En el enunciado se indica que los discos “C2” y “C3” forman un condensador; por tanto, cuando se encuentran a distinto potencial --como es el caso--, las respectivas superficies enfrentadas de los conductores están en influencia total, almacenano cantidades opuestas de carga. Además, si se trata de un condensador plano paralelo, estas cargas se distribuyen de manera practicamente uniforme en dichas superficies, y en el dieléctrico que las separa se localiza un campo eléctrico uniforme (igual módulo, dirección y sentido en todos los puntos), que es perpendicular a ambas superficies cargadas.

La relación entre la carga eléctrica en una de las superficies y su diferencia de potencial con la otra está determinada por la capacidad eléctrica del condensador, de manera que:

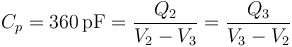
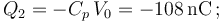
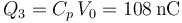
$C_p=360\,\mathrm{pF}=\frac{Q_2}{V_2-V_3}=\frac{Q_3}{V_3-V_2}$ $\Rightarrow$ $Q_2=-C_p\!\ V_0=-108\,\mathrm{nC}\!\ \mathrm{;}$ $Q_3=C_p\!\ V_0=108\,\mathrm{nC}$

2.2 Energía del sistema tras la desconexión

La energía electrostática de un sistema de conductores es igual a la mitad del producto de las cargas distribuidas en las superficies de los conductores multiplicadas por el potencial al que se encuentran éstos.

En este caso se indica que, tras cargar el sistema de conductores conectando el “C1” al generador, se procede a desconectarlo. Obsérvese que el conductor formado por la conexión de “C1” y “C2” queda aislado y, por tanto, con las mismas cargas $Q 1$ y $Q 2$ que adquirió con la conexión. El conductor “C3” permanece conectado a tierra y, en consecuencia, a potencial nulo. Pero como su cara interna se encuentra en influencia total con la del disco “C2”, debe mantener la cantidad de carga $Q 3$ , opuesta a $Q 2$ . Asimismo, como las capacidades eléctricas de conductor esférico y condensador plano no han cambiado (pues la geometría no se ha modificado), los valores de los potenciales $V 1$ y $V 2$ seguiran siendo iguales a $- V 0$ . Por tanto, tras la desconexión se tendrá:

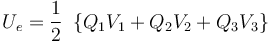
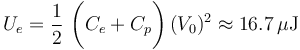
$U_e=\frac{1}{2}\ \left\{Q_1V_1+Q_2V_2+Q_3V_3\right\}$ $\Rightarrow$ $U_e=\frac{1}{2}\ \bigg(C_e+C_p\bigg)\!\ (V_0)^2\approx 16.7\,\mu\mathrm{J}$

2.3 Consecuencias de la retirada del dieléctrico

Tras cargar eléctricamente el sistema, se proceder a retirar la lámina de dieléctrico del condensador. Esto producirá un cambio en la capacidad eléctrica del condensador plano paralelo y, en consecuencia, una nueva relación entre los valores de la carga eléctrica en los conductores “C2” y “C3” y el valor del potencial en “C2” (nótese que el disco “C3” se mantiene conectado a tierra y, por tanto, a potencial nulo:

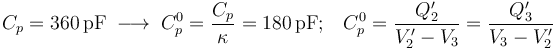
$C_p=360\,\mathrm{pF}\;\longrightarrow\; C_p^0=\frac{C_p}{\kappa}=180\,\mathrm{pF}\mathrm{;}\quad C_p^0=\frac{Q_2^\prime}{V_2^\prime-V_3}=\frac{Q_3^\prime}{V_3-V_2^\prime}$

La capacidad electrica de la esfera conductora “C1” no cambia, pero como permanece conectada al disco “C2” el potencial de aquélla cambiará si lo hace el de éste y, en consecuencia también se modificará la cantidad de carga distribuida en la superficie esférica:

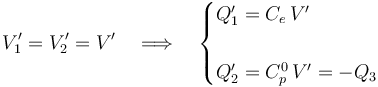
$V_1^\prime=V_2^\prime=V^\prime\quad\Longrightarrow\quad \begin{cases}Q_1^\prime=C_e\!\ V^\prime\\ \\ Q_2^\prime=C_p^0\!\ V^\prime=-Q_3\end{cases}$

El valor $V^\prime$ se determina con la condición de que, una vez desconectados del generador, lo conductores “C1” y “C2” constituyen un único conductor aislado, donde se mantiene la carga de 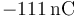$-111\,\mathrm{nC}$ :

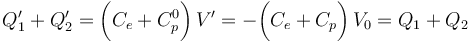
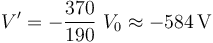
$Q_1^\prime+Q_2^\prime=\bigg(C_e+C_p^0\bigg)\!\ V^\prime=-\bigg(C_e+C_p\bigg)\!\ V_0=Q_1+Q_2$ $\Rightarrow$ $V^\prime=-\frac{370}{190}\ V_0\approx-584\,\mathrm{V}$

Es decir, el potencial electrostático en los conductores “C1” y “C2” se hace más negativo. Esto tiene como consecuencia la variación de las cantidades de carga distribuidas en los conductores:

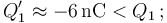
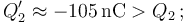
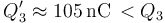
$Q_1^\prime\approx -6\,\mathrm{nC}<Q_1\!\ \mathrm{;}$ $Q_2^\prime\approx -105\,\mathrm{nC}>Q_2\!\ \mathrm{;}$ $Q_3^\prime\approx 105\,\mathrm{nC}\!\ <Q_3$

Disminuye la cantidad de carga en los conductores “C3” y “C1” (en éste se hace más negativa), y aumenta la carga en “C2” (se hace menos negativa).

2.4 Ruptura dieléctrica en el sistema

Acabamos de obtener en el apartado anterior que el potencial en los conductores “C1” y “C2” casi duplica su valor (en términos absolutos), por lo que resulta de interés analizar la posibilidad de la ruptura en alguno de los medios dieléctricos del sistema. Analicemos dicha posibilidad tanto antes como después de retirar la lámina del condensandor.

2.4.1 Antes de retirar el dieléctrico

En el entorno del conductor esférico “C1”, el módulo del campo eléctrico alcanza su valor máximo en los puntos de la superficie conductora “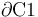 $\partial\mathrm{C1}$ ”:

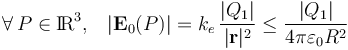
$\forall\, P\in\mathrm{I}\!\mathrm{R}^3\mathrm{,}\quad|\mathbf{E}_0(P)|=k_e\!\ \frac{|Q_1|}{|\mathbf{r}|^2}\leq \frac{|Q_1|}{4\pi\varepsilon_0R^2}$

Teniendo en cuenta cómo es la capacidad eléctrica de este conductor y cómo ésta determinar la relación entre la carga que almacena en su superficie y la diferencia de potencial a que se encuentra, podemos determinar el valor máximo del campo eléctrico en torno a la esfera “C1”:

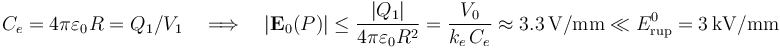
$C_e=4\pi\varepsilon_0\!\ R =Q_1/V_1\quad\Longrightarrow\quad |\mathbf{E}_0(P)|\leq \frac{|Q_1|}{4\pi\varepsilon_0R^2}=\frac{V_0}{k_e\!\ C_e}\approx 3.3\, \mathrm{V}/\mathrm{mm} \ll E_\mathrm{rup}^0=3\,\mathrm{kV}/\mathrm{mm}$

Como puede comprobarse, cuando la esfera se conecta a la fuente de 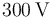$300\,\mathrm{V}$ dicho valor máximo es considerablemete inferior al campo de ruptura del aire, por lo que en esta región no se verifica ruptura dieléctrica.

En el interior del dieléctrico que rellena el condensador plano paralelo se localiza un campo eléctrico uniforme cuyo módulo es igual a la diferencia de potencial entre los conductores, dividido por la distancia $d$ que los separa. Y aunque el valor de este parámetro geométrico no se indica en el enunciado, puede determinarse a partir de la capacidad eléctrica del condensador. Como las superficies conductoras en influencia total son discos de radio 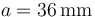$a=36\,\mathrm{mm}$ y el papel parafinado tiene una constante dieléctrica $κ = 2$ , se tendrá que:

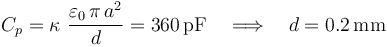
$C_p=\kappa\ \frac{\varepsilon_0\!\ \pi\!\ a^2}{d}=360\,\mathrm{pF} \quad\Longrightarrow\quad d=0.2\,\mathrm{mm}$

Por tanto, al conectar el sistema al generador y antes de retirar la lámina de papel parafinado, la intensidad del campo eléctrico entre las placas del condensador es...

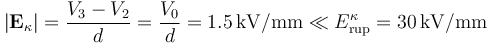
$|\mathbf{E}_\kappa|=\frac{V_3-V_2}{d}=\frac{V_0}{d}=1.5\,\mathrm{kV}/\mathrm{mm}\ll E_\mathrm{rup}^\kappa=30\,\mathrm{kV}/\mathrm{mm}$

... mucho menor que el campo de ruptura de dicho dieléctrico. Puede comprobarse que, para que se produjese tal ruptura, sería necesario que el valor $V 0$ del generador superase los 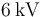$6\,\mathrm{kV}$ .

2.4.2 Tras retirar el dieléctrico

El módulo del campo eléctrico entre los discos conductores al retirar el dieléctrico es:

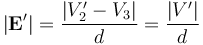
$|\mathbf{E}^\prime|=\frac{|V_2^\prime-V_3|}{d}=\frac{|V^\prime|}{d}$

En consecuencia, la condición para que no se produzca la ruptura dieléctrica entre dichos conductores es que el la intensidad de este campo uniforme no supere el valor de ruptura para el aire. Por tanto,

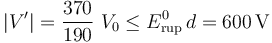
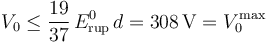
$|V^\prime|=\frac{370}{190}\ V_0\leq E_\mathrm{rup}^0\!\ d=600\,\mathrm{V}$ $\Longleftrightarrow$ $V_0\leq \frac{19}{37}\!\ E_\mathrm{rup}^0\!\ d=308\,\mathrm{V}=V_0^\mathrm{max}$

Obsérvese que para este valor de fuerza electromotriz del generador, el potencial de los conductores “C1” y “C2” sería 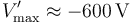$V^\prime_\mathrm{max}\approx-600\,\mathrm{V}$ . Así, la intensidad del campo eléctrico en el entorno de la esfera conductora “C1” se mantendría muy por debajo del valor de ruptura dieléctrica del aire:

$|\mathbf{E}_0^\prime(P)|\leq \frac{V_\mathrm{max}^\prime}{k_e\!\ C_e}\approx 6.7\, \mathrm{V}/\mathrm{mm} \ll E_\mathrm{rup}^0=3\,\mathrm{kV}/\mathrm{mm}$

Esfera y condensador plano paralelo, F2 GIA (Abr, 2014)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Carga eléctrica en los conductores

2.2 Energía del sistema tras la desconexión

2.3 Consecuencias de la retirada del dieléctrico

2.4 Ruptura dieléctrica en el sistema

2.4.1 Antes de retirar el dieléctrico

2.4.2 Tras retirar el dieléctrico

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES