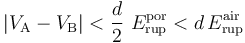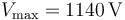Sistema electrostático de cuatro discos conductores, F2 GIA (Jun, 2013)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

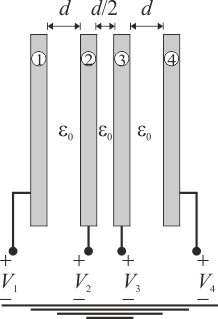
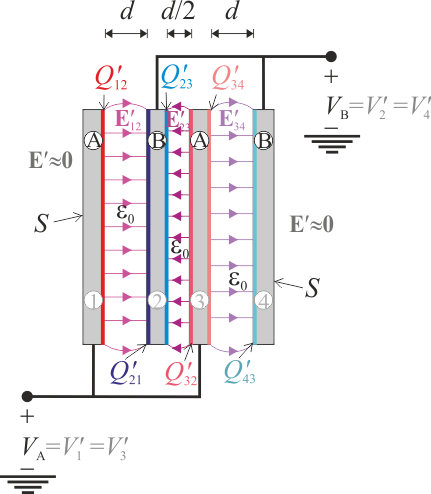
Un sistema de conductores está formado por cuatro discos metálicos idénticos, de sección $S$ , colocados con sus respectivas superficies en planos paralelos y con sus centros en el mismo eje perpendicular a los discos. Las superficies enfrentadas de los dos discos centrales, “2” y “3”, están separadas una distancia $d / 2$ , mientras que sus otras superficies se mantienen a una distancia $d$ de las de los discos “1” y “4”, colocados en los extremos del sistema. El valor de $d$ es lo suficientemente pequeño frente al diámetro y grosor de los discos como para poder considerar que cada par de superficies conductoras enfrentadas se encuentran en influencia total, formando así un condensador plano paralelo relleno de aire.

Obtenga las expresiones para la carga eléctrica total en cada uno de los discos en función de los parámetros geométricos y de los valores del potencial electrostático en los discos.
Los discos “1” y “3” se conectan mediante un cable conductor ideal, formando el conductor “A”, e igualmente se hace con “2” y “4” para forma el “B”. Justifique por qué los conductores surgidos de estas asociaciones forman un condensador y calcule su capacidad eléctrica equivalente.
Considere el caso concreto en que el radio de los discos es de 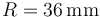$R=36\,\mathrm{mm}$ y la distancia 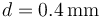$d=0.4\,\mathrm{mm}$ . Sabiendo que la ruptura dieléctrica del aire se produce para una intensidad de campo eléctrico 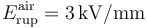$E_\mathrm{rup}^\mathrm{air}=3\,\mathrm{kV}/\mathrm{mm}$ , determine la diferencia de potencial máxima, $V max$ , que puede establecerse entre los conductores “A” y “B”. Calcule también la energía máxima que puede almacenarse en el sistema. ¿Entre qué conductores se produce la ruptura cuando se supera el valor $V max$ ?
Si entre los conductores “2” y “3” se introduce una lámina de porcelana, de constante dieléctrica $κ = 7$ y campo de ruptura 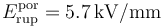$E_\mathrm{rup}^\mathrm{por}=5.7\,\mathrm{kV}/\mathrm{mm}$ , ¿cuál será el valor de $V max$ y entre qué conductores se producirá la ruptura si se supera dicho valor? ¿Cuánto vale ahora la capacidad eléctrica del sistema?

2 Solución

A modo de introducción, repasaremos los conceptos fundamentales a tener en cuenta en el planteamiento y análisis del sistema bajo estudio. Consideremos que los cuatro disco conductores del sistema descrito se hallan a sendos valores arbitrarios de potencial electrostático $V 1$ , $V 2$ , $V 3$ y $V 4$ , tomando como valor de referencia el que existe en puntos muy alejados del sistema (infinito). Como se sabe, cada disco constituye una región equipotencial y en el caso general de que estos valores sean distintos entre sí, se tendrá que entre los discos existen diferencias de potencial y, por tanto, un campo eléctrico que en cada punto coincide con el vector opuesto al gradiente de aquel campo escalar.

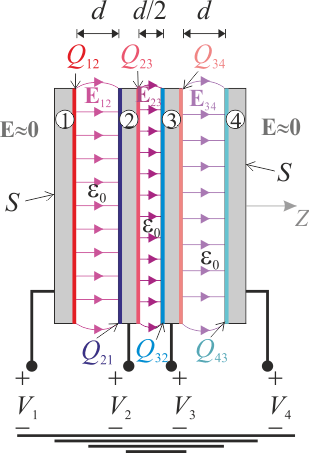
En el enunciado se indica que las distancias que separan a cada par de discos contiguos son mucho menores que las dimensiones de los discos (diámetro y grosor). Esto da lugar a que el módulo del gradiente del potencial (variación del potencial por unidad de longitud) en el espacio dieléctrico (aire) que existe entre cada par de discos contiguos sea mucho mayor que el que existe entre cada disco y el infinito. Esto es lo mismo que decir que el campo eléctrico en el sistema descrito sólo va a tener valores significativos en dichos espacios entre discos, siendo prácticamente nulo en la región exterior que rodea al sistema. Por otra parte, cuando éste se halla en equilibrio electrostático, el campo eléctrico en el interior de cada disco es estrictamente nulo, así como la densidad volumétrica de carga eléctrica neta. Sin embargo, puede haber carga eléctrica distribuida en las superficies de los discos conductores, la cuál estará necesariamente asociada a la existencia de una discontinuidad del campo eléctrico.

Obsérvese que, en virtud de la discusión que hemos realizado acerca de cómo se distribuye el campo eléctrico, en el sistema bajo estudio dicha discontinuidad se produce en las superficies o caras de cada uno de los discos que estén enfrentadas a otro disco contiguo; por el contrario, en las caras exteriores de los discos numerados como “1” y “4”, no hay tal discontinuidad y, en consecuencia, no habrá carga eléctrica superficial. Además, si asumimos que en la región exterior al sistema no hay campo eléctrico apreciable, todas las líneas de campo eléctrico que partan de una de las caras planas de un disco conductor habrán de terminar en la cara del disco contiguo que se encuentra frente a aquélla. Es decir, cada par de caras o superficies conductoras enfrentadas, separadas por aire y pertenecientes a discos contiguos, se encuentran en influencia total formando, por tanto, un condensador eléctrico. En consecuencia, dichas superficies conductoras almacenarán cantidades opuestas de carga eléctrica, de manera que si denominamos

Q i j

a la cantidad de carga eléctrica distribuida en la cara plana del disco

i

que se encuentra frente al disco

j

, se cumplirán las relaciones:

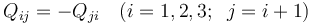
$\displaystyle Q_{ij}=-Q_{ji}\quad (i=1,2,3;\;\; j=i+1)$

Cada condensador está caracterizado por su correspondiente capacidad eléctrica, que se define como la relación entre la carga almacenada en una de los superficies o caras conductoras que lo constituyen, y la diferencia de potencial entre ambos conductores:

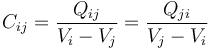
$C_{ij}=\frac{Q_{ij}}{V_i-V_j}=\frac{Q_{ji}}{V_j-V_i}$

Además, esta magnitud depende exclusivamente de la geometría del condensador y del medio dielétrico que separa a los conductores. Como hemos visto, en el sistema bajo estudio tendremos tres condensadores formados, cada uno de ellos, por dos superficies conductoras planas y paralelas muy próximas entre sí. Asumiendo que podemos aplicar la aproximación del condensador plano-paralelo, en el cuál la distribución de carga en cada superficie conductora es uniforme (se desprecian los efectos de borde), así como el campo eléctrico en el espacio dieléctrico, las capacidades de estos condensadores serán proporcionales a las áreas de las superficies conductoras e inversamente proporcionales a las distancias que las separan, siendo la constante de proporcionalidad igual a la permitividad dieléctrica del aire (que consideraremos igual a la del vacío). Se tendrá, por tanto:

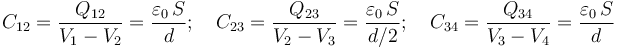
$C_{12}=\frac{Q_{12}}{V_1-V_2}=\frac{\varepsilon_0\!\ S}{d};\quad C_{23}=\frac{Q_{23}}{V_2-V_3}=\frac{\varepsilon_0\!\ S}{d/2};\quad C_{34}=\frac{Q_{34}}{V_3-V_4}=\frac{\varepsilon_0\!\ S}{d}$

Nótese que los condensandores de capacidades $C 12$ y $C 23$ siempre están conectados ya que ambos comparten el disco conductor “2”, y aunque les corresponden superficies conductoras distintas de éste, siempre serán equipotenciales. Sin embargo, esto no implica que estén conectados en serie, pues no se indica que dicho disco conductor se encuentre aislado y descargado. Esta misma situación se verifica en el caso del disco “3” y los condensadores $C 23$ y $C 34$ .

Por otra parte, la aproximación del condensador plano-paralelo tiene como consecuencia que el campo eléctrico entre cada par de discos contiguos sea prácticamente uniforme; es decir, constante en módulo, sentido y dirección, siendo ésta perpendicular a las superficies planas de los discos. Sea $\mathbf{E}_{ij}$ el vector del campo eléctrico existente en la región dieléctrica (aire en nuestro caso) que separa el disco $i$ del contiguo $j$ , se tendrá:

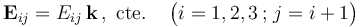
$\mathbf{E}_{ij}=E_{ij}\!\ \mathbf{k}\,\mathrm{,}\,\,\,\mathrm{cte}.\quad\, \big(i=1,2,3\,\mathrm{;}\, \, j=i+1\big)$

Obtengamos el valor de la componente $E i j$ , constante entre cada par de discos, en términos de la diferencia de pontencial entre éstos:

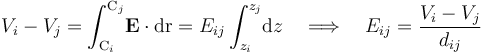
$V_i-V_j=\int_{\mathrm{C}_i}^{\mathrm{C}_j}\!\mathbf{E}\cdot\mathrm{d}\mathrm{r}=E_{ij}\int_{z_i}^{z_j}\!\mathrm{d}z\quad\Longrightarrow\quad E_{ij}=\frac{V_i-V_j}{d_{ij}}$

siendo $d i j$ la distancia que los separa o, lo que es lo mismo, el espesor del medio dieléctrico existente entre las superficies conductoras enfrentadas y en influencia total.

2.1 Carga eléctrica en cada disco

A partir del análisis realizado en el anterior preámbulo, la resolución de los diferentes apartados del ejercicio es casi inmediata. En primer lugar se solicita la cantidad total de carga que habrá almancenada en cada uno de los cuatros discos conductores, en función del potencial a que se encuentren como resultado, por ejemplo, de que éstos se hallen conectados a sendas fuentes que fijan valores constantes de potencial. La carga total en cada disco será igual a la suma de las cargas distribuidas en su superficie.

Si denominamos $Q i$ a la cantidad total de carga en el disco $i$ -ésimo, y teniendo en cuenta la discusión previa, se tendrá que

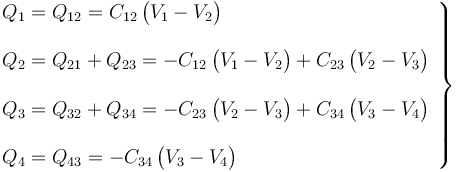
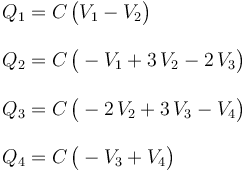
$\left.\begin{array}{l}Q_1=Q_{12}=C_{12}\!\ \big(V_1-V_2\big)\\ \\ Q_2=Q_{21}+Q_{23}=-C_{12}\!\ \big(V_1-V_2\big)+C_{23}\!\ \big(V_2-V_3\big)\\ \\ Q_3=Q_{32}+Q_{34}=-C_{23}\!\ \big(V_2-V_3\big)+C_{34}\!\ \big(V_3-V_4\big)\\ \\ Q_4=Q_{43}=-C_{34}\!\ \big(V_3-V_4\big) \end{array}\right\}$ $\Rightarrow$ $\begin{array}{l}Q_1=C\!\ \big(V_1-V_2\big)\\ \\ Q_2=C\!\ \big(-V_1+3\!\ V_2-2\!\ V_3\big)\\ \\ Q_3=C\!\ \big(-2\!\ V_2+3\!\ V_3-V_4\big)\\ \\ Q_4=C\!\ \big(-V_3+V_4\big) \end{array}$

donde $C$ es el parámetro característico del sistema, con dimensiones de capacidad eléctrica, que depende de la geometría del mismo:

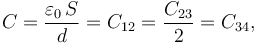
$C=\frac{\varepsilon_0\!\ S}{d}=C_{12}=\frac{C_{23}}{2}=C_{34},$

2.2 Conexión de los discos. Condensador equivalente

Se procede ahora a conectar los discos “1” y “3” mediante un cable conductor, de manera que constituyan una región equipotencial que denominaremos “A”; también se realiza idéntica operación con los discos conductores “2” y “4”, para crear la región equipotencial “B”.

Obsérvese que el sistema de conductores resultante puede considerarse como un caso particular de la configuración general analizada en el preámbulo y el apartado anterior. Se trataría de la situación en la cuál los valores del potencial de los cuatro discos verifican las siguientes relaciones:

$V_1^\prime=V_3^\prime=V_\mathrm{A}\,\mathrm{,}\qquad\qquad V_2^\prime=V_4^\prime=V_\mathrm{B}$

Si, en general, los valores de potencial $V A$ y $V B$ son distintos, entre cada par de discos contiguos habrá una diferencia de potencial no nula y, en consecuencia, existirá campo eléctrico en la regiones de aire localizadas entre aquéllos. Como se discutió anteriormente, esto determinará la presencia de distribuciones superficiales de carga en aquellas caras de cada disco conductor que se encuentren enfrentadas a otro disco. Además, como la geometría del sistema no ha cambiado, se seguirá verificando que el campo eléctrico en la región exterior al sistema de conductores es prácticamente nulo, por lo que las caras externas de los discos “1” y “4” seguirán descargadas. También se seguirá cumpliendo que cada par de caras enfrentadas de discos contiguos se encontrarán en influencia total, de manera que almacenarán cantidades opuestas de carga eléctrica superficial:

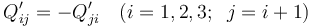
$\displaystyle Q_{ij}^\prime=-Q_{ji}^\prime\quad (i=1,2,3;\;\; j=i+1)$

Y como las secciones de los discos no han cambiado, ni el espesor de las capas de aire que los separan, estas nuevas cantidades de carga y la diferencia de potencial entre los discos seguirán verificando la misma relación que antes de proceder a la conexión de los discos; es decir:

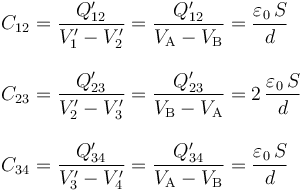
$\begin{array}{l}\displaystyle C_{12}=\frac{Q_{12}^\prime}{V_1^\prime-V_2^\prime}=\frac{Q_{12}^\prime}{V_\mathrm{A}-V_\mathrm{B}}=\frac{\varepsilon_0\!\ S}{d}\\ \\ \displaystyle C_{23}=\frac{Q_{23}^\prime}{V_2^\prime-V_3^\prime}=\frac{Q_{23}^\prime}{V_\mathrm{B}-V_\mathrm{A}}=2\!\ \frac{\varepsilon_0\!\ S}{d}\\ \\ \displaystyle C_{34}=\frac{Q_{34}^\prime}{V_3^\prime-V_4^\prime}=\frac{Q_{34}^\prime}{V_\mathrm{A}-V_\mathrm{B}}=\frac{\varepsilon_0\!\ S}{d} \end{array}$

Pero analicemos el sistema considerándolo formado por dos regiones conductoras, “A” y “B”, separadas por aire. Si despreciamos la cantidad de carga eléctrica que puediera almacenarse en los cables de conexión, se tendrá que las cantidades totales de carga eléctrica, $Q A$ y $Q B$ , distribuidas en dichas regiones serán iguales a la suma de las cargas superficiales que hay en los correspondientes discos que las forman. Y teniendo en cuenta la propiedad descrita anteriormente de que las cargas en superficies enfrentadas son opuestas, se obtiene:

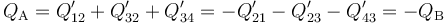
$\displaystyle Q_\mathrm{A}=Q_{12}^\prime+Q_{32}^\prime+Q_{34}^\prime=-Q_{21}^\prime-Q_{23}^\prime-Q_{43}^\prime=-Q_\mathrm{B}$

Es decir, las regiones conductoras “A” y “B” creadas al conectar los discos almacenan cantidades opuestas de carga. Esto esto está directamente relacionado con que dichas regiones conductoras se hallan en influencia total pues, como justificamos anteriormente, toda línea de campo eléctrico que parte de la región “A” (discos “1” y “3”) ha de terminar necesariamente en algún punto de la región “B” (discos “2” y “4”). Por tanto, los conductores “A” y “B”, separados por un dieléctrico (aire), constituyen un condensador cuya capacidad eléctrica es igual a la relación entre la carga almancenada en una de las regiones conductoras, y su diferencia de potencial con la otra:

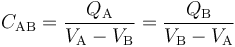
$C_\mathrm{AB}=\frac{Q_\mathrm{A}}{V_\mathrm{A}-V_\mathrm{B}}=\frac{Q_\mathrm{B}}{V_\mathrm{B}-V_\mathrm{A}}$

El valor de este parámetro debe depender exclusivamente de la geométria del sistema. Para obtenerlo, no tenemos más que determinar el valor de la carga en el conductor “A” en función de la diferencia de potencial de éste con el “B”; utilizando resultados anteriores:

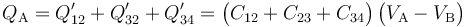
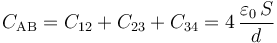
$Q_\mathrm{A}=Q_{12}^\prime+Q_{32}^\prime+Q_{34}^\prime=\big(C_{12}+C_{23}+C_{34}\big)\!\ \big(V_\mathrm{A}-V_\mathrm{B}\big)$ $\quad$ $\Rightarrow$ $\quad$ $C_\mathrm{AB}=C_{12}+C_{23}+C_{34}=4\!\ \frac{\varepsilon_0\!\ S}{d}$

Obsérvese este resultado nos permite extraer la conclusión de que el sistema de conductores que se obtiene al conectar los discos es un condensador eléctrico equivalente a la asociación en paralelo de los tres condensadores que forman los pares de superficies conductoras enfrentadas.

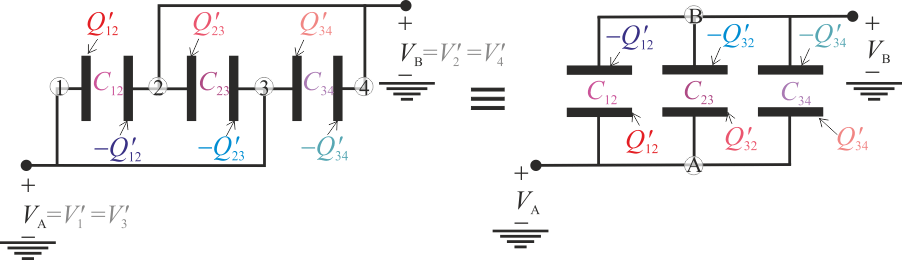
2.3 Diferencia de potencial máxima entre conductores

Una vez establecidas las conexiones entre los discos “1-3” y “2-4” para configurar las regiones conductoras “A” y “B”, los campos eléctricos entre pares cada par de discos contiguos, expresados en términos de la diferencia de potencial entre dichas regiones, serán de la forma:

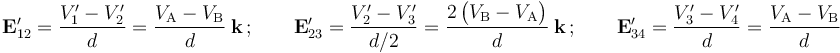
$\mathbf{E}_{12}^\prime=\frac{V_1^\prime-V_2^\prime}{d}=\frac{V_\mathrm{A}-V_\mathrm{B}}{d}\ \mathbf{k}\,\mathrm{;}\,\qquad \mathbf{E}_{23}^\prime=\frac{V_2^\prime-V_3^\prime}{d/2}= \frac{2\!\ \big(V_\mathrm{B}-V_\mathrm{A}\big)}{d}\ \mathbf{k}\,\mathrm{;}\,\qquad \mathbf{E}_{34}^\prime=\frac{V_3^\prime-V_4^\prime}{d}=\frac{V_\mathrm{A}-V_\mathrm{B}}{d}$

Pero si los espacios interdiscos estén rellenos por un medio material dieléctrico, como es el caso, los módulos o intensidad de dichos campos no pueden superar un valor crítico

E rup

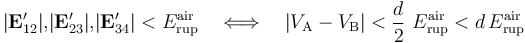
, por encima del cuál se produce la ruptura dieléctrica del medio. Como los tres medios son aire, se tendrá: $|\mathbf{E}_{12}^\prime|\mathrm{,}|\mathbf{E}_{23}^\prime|\mathrm{,}|\mathbf{E}_{34}^\prime|<E_\mathrm{rup}^\mathrm{air}\quad\Longleftrightarrow\quad |V_\mathrm{A}-V_\mathrm{B}|<\frac{d}{2}\ E_\mathrm{rup}^\mathrm{air} < d\!\ E_\mathrm{rup}^\mathrm{air}$

Y teniendo en cuenta el valor del campo de ruptura del aire y del parámetro $d$ , se obtiene las diferencia de potencial máxima que puede existir entre los conductores “A” y “B”:

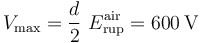
$V_\mathrm{max}=\frac{d}{2}\ E_\mathrm{rup}^\mathrm{air}= 600\,\mathrm{V}$

Un valor igual o superior a éste provocaría, en primer lugar, la ruptura dieléctrica ente los discos “2” y “3”.

La energía electrostática almacenada en un sistema de conductores y dieléctricos es igual a la semisuma del producto de las cargas almacenadas multiplicadas por el valor de los potenciales. En el sistema bajo estudio, y tras realizar la conexión de los discos, se tendrá:

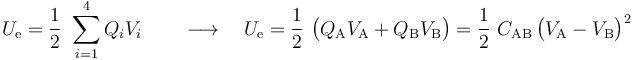
$U_\mathrm{e}=\frac{1}{2}\ \sum_{i=1}^4Q_iV_i\qquad\longrightarrow\quad U_\mathrm{e}=\frac{1}{2}\ \big(Q_\mathrm{A}V_\mathrm{A}+Q_\mathrm{B}V_\mathrm{B}\big)=\frac{1}{2}\ C_\mathrm{AB}\!\ \big(V_\mathrm{A}-V_\mathrm{B}\big)^2$

En consecuencia, la existencia de un valor máximo para la diferencia de potencial entre los conductores “A” y “B” tendrá como consecuencia una limitación en la cantidad de energía electrostrática que puede almacenarse en el sistema. Sustituyendo los valores de $d$ , $\varepsilon_0$ , y del radio de los discos para determinar su sección $S$ , se obtiene:

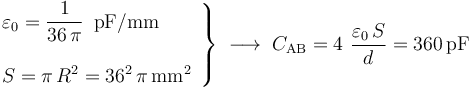
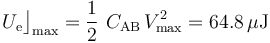
$\left.\begin{array}{l}\displaystyle \varepsilon_0=\frac{1}{36\!\ \pi}\,\ \mathrm{pF}/\mathrm{mm}\\ \\ \displaystyle S=\pi\!\ R^2=36^2\!\ \pi\,\mathrm{mm}^2\end{array}\right\}\;\longrightarrow\; C_\mathrm{AB}=4\ \frac{\varepsilon_0\!\ S}{d}=360\,\mathrm{pF}$ $\Rightarrow$ $U_\mathrm{e}\big\rfloor_\mathrm{max}=\frac{1}{2}\ C_\mathrm{AB}\!\ V_\mathrm{max}^2=64.8\,\mu\mathrm{J}$

2.4 Efecto de la lámina de porcelana

En este último apartado se analizan los cambios que se produce en el sistema electrostático cuando en la configuración de conductores “A” y “B” se introduce una lámina dieléctrica de porcelana, cuya constante dieléctrica y campo de ruptura tienen los valores $κ = 7$ y 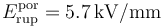$E_\mathrm{rup}^\mathrm{por}=5.7\,\mathrm{kV}/\mathrm{mm}$ .

En el nuevo sistema, las caras enfrentadas de cada par de discos contiguos siguen estando en influencia total formando, por tanto, tres condesadores planos paralelos. De hecho, los que se forman entre los discos “1” y “2”, y “3” y “4”, incluso mantienen los mismo valores de capacidad,

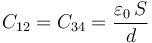
$C_{12}=C_{34}=\frac{\varepsilon_0\!\ S}{d}$

pues siguen estando rellenos de aire y se mantienen el valor $S$ del área tamaño de los discos y las distancias $d$ de separación. Por el contrario, la introducción de la lámina de porcelana rellenando el espacio de separación entre los discos “2” y “3”, pero sin cambiar éstos ni la distancia que los separa, produce un cambio en la capacidad de este condensador, que resulta multiplicada por un factor $κ$ :

$C_{23}^\prime=\kappa\!\ C_{23}=2\!\ \kappa\ \frac{\varepsilon_0\!\ S}{d}$

Y como se mantienen conectados los discos “1” y “3”, formando la región conductora “a”, y los “2” y “4”, para formar el conductor “B”, éstas siguen constituyendo un condensador, equivalente a la conexión en paralelo de los tres condensadores planos paralelos descritos. Su capacidad eléctrica es:

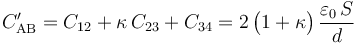
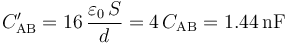
$C_{\mathrm{A}\mathrm{B}}^\prime=C_{12}+\kappa\!\ C_{23}+C_{34}=2\!\ \big(1+\kappa\big)\!\ \frac{\varepsilon_0\!\ S}{d}$ $\Rightarrow$ $C_{\mathrm{A}\mathrm{B}}^\prime=16\!\ \frac{\varepsilon_0\!\ S}{d}=4\!\ C_{\mathrm{A}\mathrm{B}}=1.44\,\mathrm{nF}$

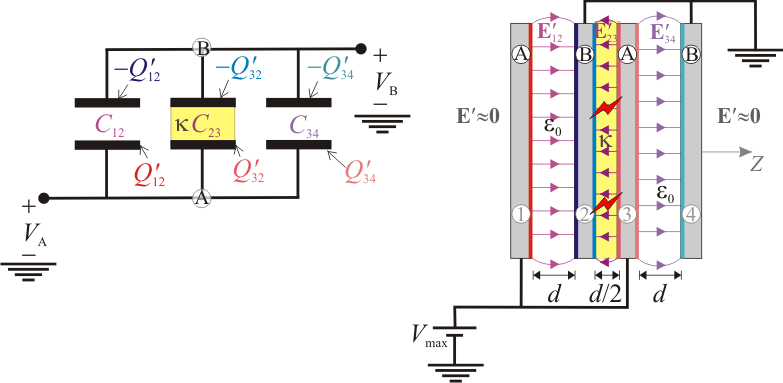
Analicemos ahora el efecto de la introducción de la lámina sobre el valor máximo de diferencia de potencial que se puede establecer entre los conductores “A” y “B”. Recuérdese que en el anterior apartado dicha $V max$ estaba determinada por la ruptura dieléctrica entre los discos más proximos entre sí: el “2” y el “3”. Al introducir la porcelana entre ambos discos, aumentará el valor del campo de ruptura entre ellos y, en consecuencia, la diferencia de potencial máxima aplicable. Como entre los discos “1” y “2”, así como entre “3” y “4”, sigue habiendo aire, se deberán cumplir las siguientes relaciones simultáneamente:

$\begin{array}{rcl}\displaystyle |\mathbf{E}_{12}^\prime|=|\mathbf{E}_{34}^\prime|=\frac{|V_\mathrm{A}-V_\mathrm{B}|}{d}<E_\mathrm{rup}^\mathrm{air}&\Longleftrightarrow & |V_\mathrm{A}-V_\mathrm{B}|< d\!\ E_\mathrm{rup}^\mathrm{air}= 1.2\,\mathrm{kV}\\ \\ \displaystyle |\mathbf{E}_{23}^\prime|=\frac{|V_\mathrm{A}-V_\mathrm{B}|}{d/2}<E_\mathrm{rup}^\mathrm{por}&\Longleftrightarrow &\displaystyle |V_\mathrm{A}-V_\mathrm{B}|< \frac{d}{2}\ E_\mathrm{rup}^\mathrm{por}= 1.14\,\mathrm{kV} \end{array}$

Es decir, a pesar de haber introducido la lámina de porcelana, sigue siendo la ruptura dieléctrica entre los discos “2” y “3” lo que conduciona el valor máximo de diferencia de potencial, si bien éste ha aumentado respecto del caso analizado en los anteriores apartados:

$|V_\mathrm{A}-V_\mathrm{B}|< \frac{d}{2}\ E_\mathrm{rup}^\mathrm{por}< d\!\ E_\mathrm{rup}^\mathrm{air}$ $\quad$ $\Rightarrow$ $\quad$ $V_\mathrm{max}= 1140\,\mathrm{V}$

Sistema electrostático de cuatro discos conductores, F2 GIA (Jun, 2013)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Carga eléctrica en cada disco

2.2 Conexión de los discos. Condensador equivalente

2.3 Diferencia de potencial máxima entre conductores

2.4 Efecto de la lámina de porcelana

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES