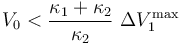Condensadores en asociación variable, F2 GIA (Sept, 2018)

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

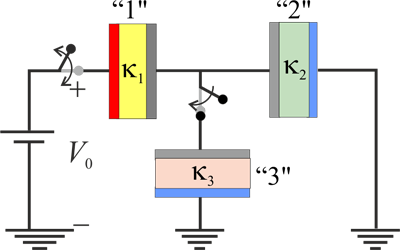
Se tienen tres condensadores de idéntica geometría, “1”, “2” y “3”, cuya capacidad eléctrica sería $C 0$ si no hubiese ningún medio material dieléctrico separando los conductores. Sin embargo, están rellenos de sendos dieléctricos de constantes dieléctricas $κ 1$ , $κ 2$ y $κ 3$ , respectivamente. Inicialmente se encuentran los tres descargados y los dos primeros están conectados en serie, con el conductor libre de “2” conectado al conductor de referencia o tierra. Un generador electrostático de f.e.m. $V 0$ , tiene su electrodo negativo conectado también al conductor de referencia. Se procede a conectar el electrodo positivo al conductor libre del condensador “1” para cargar la asociación en serie. Una vez realizado este paso, se desconecta el generador. Posteriormente, se conecta el conductor flotante de la asociación en serie formada por “1” y “2” a un conductor del condensador “3”, que tiene el otro conductor conectado a “tierra”.

¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de estos dos condensadores? ¿Cuál es el valor del potencial en el conductor flotante?
¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador?
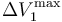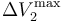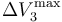Sean $\Delta V_1^\mathrm{max}$ , $\Delta V_2^\mathrm{max}$ y $\Delta V_3^\mathrm{max}$ los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener $V 0$ , en función de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que $κ 1 < κ 2 < κ 3$ y 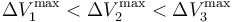$\Delta V_1^\mathrm{max}<\Delta V_2^\mathrm{max}<\Delta V_3^\mathrm{max}$ : ¿cuál debe ser el valor máximo de $V 0$ ?

2 Solución

Los valores $C i$ de Las capacidade de los tres condensadores verifican

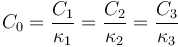
$C_0=\frac{C_1}{\kappa_1}=\frac{C_2}{\kappa_2}=\frac{C_3}{\kappa_3}$

Inicialmente, antes de realizar ninguna conexión, el sistema está completamente descargado; es decir, ambos conductores de los tres condensadores tienen carga nula y se encuentran a potencial cero.

2.1 Cargas eléctricas y potencial en la asociación en serie

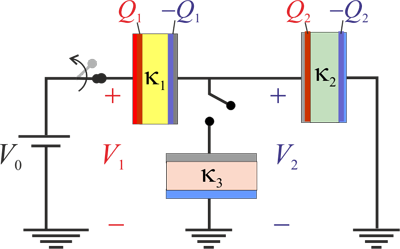
Los condensadores “1” y “2” están conectados en serie, mient ras que “3” se mantiene desconectado del sistema. En un determinado instante, se procede a conectar el electrodo accesible del condensador “1” al generador electrostático con f.e.m. de valor $V 0$ . Dicho electrodo (conductor) va a constituir una superficie equipotencial de valor $V 1$ , y se cargará con una cierta cantidad de carga $Q 1$ , suministrada por el generador; el otro electrodo del condensador “1” adquiere una cantidad de carga opuesta, por estar ambos en influencia total. Este segundo eléctrodo presentarán un valor de potencial $V 2$ , que será el mismo que el electrodo del condensador “2”, al cuál está aquél conectado, dando lugar a la asociación en serie. Y como el otro electrodo del condensador “2” está conectado a tierra y por tanto, el valor del potencial en dicho conductor es nulo, la diferencia de potencial entre dichos electrodos provoca la aparición de cargas eléctricas, naturalmente opuestas 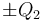$\pm Q_2$ en ambos conductores del condensador “2”. Nótese que la carga $- Q 2$ en el electrodo conectado a tierra sería suministrada por dicho conductor de referencia. Por otra parte, nótese que en la asociación en serie de ambos condensadores, los electrodos de unos y otro que son interconectados constituyen un conductor flotante; es decir, es conductor aislado en el que la carga $Q f$ que almacenada permanece constante: y si inicilamente estaba descargado, en todo momento permancerá con carga total nula, independientemente de cómo se distribuya. En consecuencia,

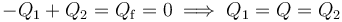
$-Q_1+Q_2=Q_\mathrm{f}=0\; \Longrightarrow \; Q_1=Q=Q_2$

Por otra parte, la capacidad $C 12$ de la asociación en serie de los condensadores 1 y 2, será

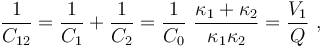
$\frac{1}{C_{12}}=\frac{1}{C _1}+\frac{1}{C_2}=\frac{1}{C_0}\ \frac{\kappa_1+\kappa_2}{\kappa_1\kappa_2}=\frac{V_1}{Q}\ \mathrm{,}$

pues la diferencia de potencial entre los conductores accesibles de la asociación es $V 1$ , al estar el otro a potencial nulo (conectado a tierra). Y puesto que el conductor accesible del condensador “1” está directamente conectado al electrodo positivo del generador mientras que el negativo está a tierra, se tendrá:

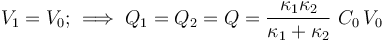
$V_1=V_0\mathrm{;}\; \Longrightarrow \; Q_1=Q_2=Q=\frac{\kappa_1\kappa_2}{\kappa_1+\kappa_2}\ C_0\!\ V_0$

El valor del potencial en el conductor flotante, $V f$ , es inmediato:

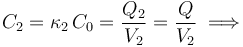
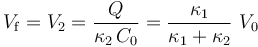
$C_2=\kappa_2\!\ C_0=\frac{Q_2}{V_2}=\frac{Q}{V_2}\; \Longrightarrow \;$ $V_\mathrm{f}=V_2=\frac{Q}{\kappa_2\!\ C_0}=\frac{\kappa_1}{\kappa_1+\kappa_2}\ V_0$

Si tras cargarse la asociación en serie se desconecta el generador, en los conductores permanecen las mismas cantidades de carga que se establecieron tras la conexión. Y tampoco lo harán los valores de los potenciales $V 1$ y $V 2$ , mientras no se mantengan las capacidades eléctricas del sistema; es decir, mientras no se cambie la geometría de los condensadores y/o sus conexiones. La energía electrostática almacenada en el sistema es

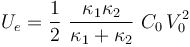
$U_e=\frac{1}{2}\ \bigg[Q_1(V_1-V_2)+Q_2V_2\bigg]=\frac{1}{2}\ \frac{Q^2}{C_{12}}\;\;\;\;\; \Longrightarrow \;$ $U_e=\frac{1}{2}\ \frac{\kappa_1\kappa_2}{\kappa_1+\kappa_2}\ C_0\!\ V_0^2$

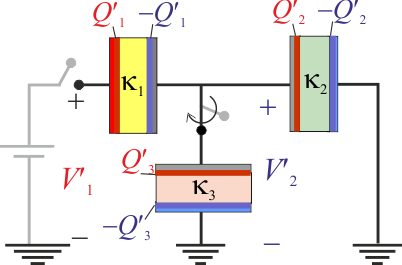
2.2 Cargas eléctricas y potenciales tras conectar el tercer condensador

Cuando el condensador “3” se conecta a la asociación en serie previamente cargada y desconectada del generador, aquél pasa de estar descargado a tener cargas 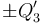$\pm Q_3^\prime$ ; pero también han cambiado las capacidades eléctricas del sitema previo, por lo que también cambiarán las cargas y potenciales, en los conductores de los condesadores “1” y “2” que, en general, tendrán valores 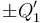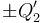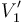$\pm Q_1^\prime$ , $\pm Q_2^\prime$ , $V_1^\prime$ y $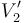V_2^\prime$ . Obsérvese que éste va a ser también el potencial en el electrodo del condensador “3” que se conecta al conductor flotante la previa asociación en serie. Y como el condensador “3” estaba inicialmente descargado, la conexión de los tres conductores (uno de cada condensador) seguirá constituyendo un conductor aislado y descargado; es decir, sigue siendo un conductor flotante. Por tanto,

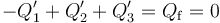
$-Q_1^\prime+Q_2^\prime+Q_3^\prime=Q_\mathrm{f}=0$

Por otra parte, el conductor libre del condensador “1” (el que se conecto y desconectó luego del generador), se encuentra aislado, es decir, no puede cambiar la cantidad de carga que soporta, que seguirá siendo la que adquirió al conectar el generador. Y en el otro conductor se mantedrá la carga opuesta, al ser “1” un condensador que, necesariamente ha de cumplir la condición de conductores en influencia total. En consecuencia, se tendrá:

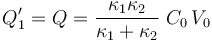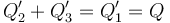
$Q_1^\prime=Q=\frac{\kappa_1\kappa_2}{\kappa_1+\kappa_2}\ C_0\!\ V_0$ y $Q_2^\prime+Q_3^\prime=Q_1^\prime=Q$

Si tenemos en cuenta que “2” y “3” forman una asociación en paralelo, su capacidad $C 23$ , es ...

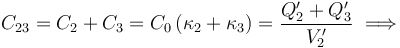
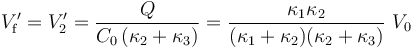
$C_{23}=C_2+C_3=C_0\!\ (\kappa_2+\kappa_3)=\frac{Q_2^\prime+Q_3^\prime}{V_2^\prime}\; \Longrightarrow \;$ $\quad V_\mathrm{f}^\prime=V_2^\prime=\frac{Q}{C_0\!\ (\kappa_2+\kappa_3)}=\frac{\kappa_1\kappa_2}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ V_0$

... y las cargas en los conductores “2” y “3”...

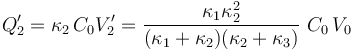
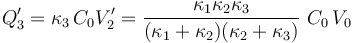
$Q_2^\prime=\kappa_2\!\ C_0 V_2^\prime=\frac{\kappa_1\kappa_2^2}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ C_0\!\ V_0$ $Q_3^\prime=\kappa_3\!\ C_0 V_2^\prime=\frac{\kappa_1\kappa_2\kappa_3}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ C_0\!\ V_0$

Finalmente, la diferencia de potencial entre los conductores del condensador “1” está determinada por la cantidad de carga eléctrica que separa y su capacidad:

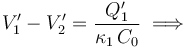
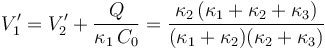
$V_1^\prime-V_2^\prime=\frac{Q_1^\prime}{\kappa_1\!\ C_0}\; \Longrightarrow \;$ $V_1^\prime=V_2^\prime+\frac{Q}{\kappa_1\!\ C_0}=\frac{\kappa_2\!\ (\kappa_1+\kappa_2+\kappa_3)}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}$

La energía electrostática almacenada en el sistema en este caso es:

$U_e=\frac{1}{2}\ \bigg[Q_1^\prime(V_1^\prime-V_2^\prime)+(Q_2^\prime+Q_3^\prime)V_2^\prime\bigg]\mathrm{,}...$

... o también, expresada en términos de la capacidad $C eq$ de la asociación en serie del condensador “1” con la asociación en paralelo de los condensadores “2” y “3”.

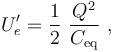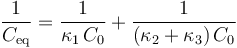
$U_e^\prime=\frac{1}{2}\ \frac{Q^2}{C_\mathrm{eq}}\ \mathrm{,}$ con $\frac{1}{C_\mathrm{eq}}=\frac{1}{\kappa_1\!\ C_0}+\frac{1}{(\kappa_2+\kappa_3)\!\ C_0}$

Luego, la variación sufrida por la energía almacenada en el sistema al conecta el tercer condensador en el sistema aislado previo, es:

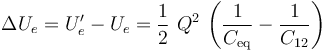
$\Delta U_e=U_e^\prime-U_e=\frac{1}{2}\ Q^2\!\ \left(\frac{1}{C_\mathrm{eq}}-\frac{1}{C_{12}}\right)$

Se tendrá, por tanto,

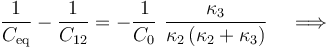
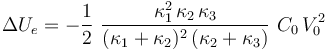
$\frac{1}{C_\mathrm{eq}}-\frac{1}{C_{12}}=-\frac{1} {C_0}\ \frac{\kappa_3}{\kappa_2\!\ (\kappa_2+\kappa_3)}\;\;\;\;\Longrightarrow$ $\Delta U_e= -\frac{1}{2}\ \frac{\kappa_1^2\!\ \kappa_2\!\ \kappa_3}{(\kappa_1+\kappa_2)^2\!\ (\kappa_2+\kappa_3)}\ C_0\!\ V_0^2$

2.3 Valor máximo de la f.e.m . del generador para evitar la ruptura dieléctrica en los condesadores

Para que no se produzca dicho fenómeno, es necesario que la diferencia de potencial en cada condensador, en cada una de las dos situaciones consideradas, sea menor que el límite máximo correspondiente.

En el primer condensador, la diferencia de potencial entre sus electrodos es la misma en las dos configuaciones consideraras; por tanto, para que no se produzca la ruptura dieléctrica en dicho condensador se deberá cumplir:

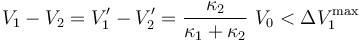
$V_1-V_2=V_1^\prime-V_2^\prime=\frac{\kappa_2}{\kappa_1+\kappa_2}\ V_0<\Delta V_1^\mathrm{max}$

El valor del potencial en el conductor flotante verifica la relación...

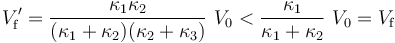
$V_\mathrm{f}^\prime =\frac{\kappa_1\kappa_2}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ V_0< \frac{\kappa_1}{\kappa_1+\kappa_2}\ V_0 =V_\mathrm{f}$

Por tanto, la diferencia de potencial en el condensador “2” alcanza el mayor valor en la configuración de asociación en serie con “1”:

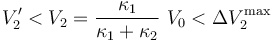
$V_2^\prime<V_2=\frac{\kappa_1}{\kappa_1+\kappa_2}\ V_0<\Delta V_2^\mathrm{max}$

En el caso del condensador “3”, éste sólo interviene en la configuración final del sistema, por tanto, debe cumplirse:

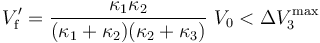
$V_\mathrm{f}^\prime =\frac{\kappa_1\kappa_2}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ V_0<\Delta V_3^\mathrm{max}$

Si se tienen en cuenta las relaciones entres los valores de las constantes dieléctricas y entre los valores de potencial máximo en cada uno de los condensadores....

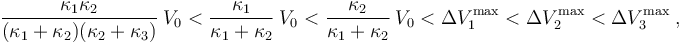
$\frac{\kappa_1\kappa_2}{(\kappa_1+\kappa_2)(\kappa_2+\kappa_3)}\ V_0<\frac{\kappa_1}{\kappa_1+\kappa_2}\ V_0<\frac{\kappa_2}{\kappa_1+\kappa_2}\ V_0<\Delta V_1^\mathrm{max}<\Delta V_2^\mathrm{max}<\Delta V_3^\mathrm{max}\ \mathrm{,}$

luego, la condición crítica en el valor $V 0$ de la f.e.m. del generador para que no se produzca la ruptura dieléctrica en el sistema es:

$V_0<\frac{\kappa_1+\kappa_2}{\kappa_2}\ \Delta V_1^\mathrm{max}$

Condensadores en asociación variable, F2 GIA (Sept, 2018)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Cargas eléctricas y potencial en la asociación en serie

2.2 Cargas eléctricas y potenciales tras conectar el tercer condensador

2.3 Valor máximo de la f.e.m . del generador para evitar la ruptura dieléctrica en los condesadores

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES