Problemas de procesos en gases ideales (GIA)
De Laplace
| Línea 14: | Línea 14: | ||
#Expansión adiabática. | #Expansión adiabática. | ||
| + | ==[[Obtención_de_las_capacidades_caloríficas_de_un_gas,_F2_GIA_(Nov,_2012)|Obtención de las capacidades caloríficas de un gas]]== | ||
| + | En el interior de un recipiente, cerrado mediante un pistón móvil, hay <math>4.48</math> litros de un gas ideal que inicialmente se encuentra a la presión de <math>1\,\mathrm{atm}</math> y <math>0{}^\mathrm{o}\,\mathrm{C}</math> de temperatura. Las paredes del recipiente y el pistón pueden considerarse perfectamente impermeables al calor. Para determinar las características del gas se desplaza el pistón | ||
| + | de manera cuasiestática, comprimiendo aquél hasta que su volumen se reduce a la mitad del inicial. Se mide la presión y se comprueba que ésta es ahora <math>2.64\,\mathrm{atm}.</math> | ||
| + | # ¿Cuál es el valor del coeficiente adiabático del gas? ¿Puede decir si se trata de un gas monoatómico o diatómico? | ||
| + | # Determine los valores de las capacidades caloríficas y los calores específicos molares del gas. | ||
| + | |||
| + | '''Dato''': <math>R=0.082\,\mathrm{atm\, l}/(\mathrm{mol\, K})=8.314\,\mathrm{J}/(\mathrm{mol\, K})</math> | ||
= Otros ejercicios = | = Otros ejercicios = | ||
Revisión de 19:12 21 may 2014
Contenido |
1 Problemas del boletín
1.1 Incremento de energía interna y trabajo en proceso isóbaro
Una cantidad fija de n moles de gas ideal sufre una transformación cuasiestática a presión constante P0, entre el estado inicial A(VA;TA), y el final B(VB;TB). ¿Cuál es la variación de energía interna experimentada por el gas en el proceso? ¿Qué cantidad de trabajo se ha transferido al sistema?
1.2 Expansión isoterma y adiabática
Un gas ideal monoatómico ocupa un volumen de 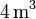 a la presión de
a la presión de 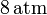 y a la temperatura de
y a la temperatura de
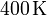 . El gas se expande hasta la presión final de
. El gas se expande hasta la presión final de
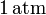 mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
mediante un proceso cuasiestático. Calcule el
trabajo realizado, el calor absorbido y la variación de energía interna en
los siguientes casos:
- Expansión isoterma.
- Expansión adiabática.
1.3 Obtención de las capacidades caloríficas de un gas
En el interior de un recipiente, cerrado mediante un pistón móvil, hay 4.48 litros de un gas ideal que inicialmente se encuentra a la presión de 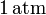 y
y 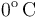 de temperatura. Las paredes del recipiente y el pistón pueden considerarse perfectamente impermeables al calor. Para determinar las características del gas se desplaza el pistón
de manera cuasiestática, comprimiendo aquél hasta que su volumen se reduce a la mitad del inicial. Se mide la presión y se comprueba que ésta es ahora
de temperatura. Las paredes del recipiente y el pistón pueden considerarse perfectamente impermeables al calor. Para determinar las características del gas se desplaza el pistón
de manera cuasiestática, comprimiendo aquél hasta que su volumen se reduce a la mitad del inicial. Se mide la presión y se comprueba que ésta es ahora 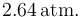
- ¿Cuál es el valor del coeficiente adiabático del gas? ¿Puede decir si se trata de un gas monoatómico o diatómico?
- Determine los valores de las capacidades caloríficas y los calores específicos molares del gas.
Dato: 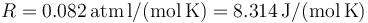
2 Otros ejercicios
2.1 Trabajo en un ciclo de un gas perfecto
Las condiciones iniciales del estado de un gas perfecto son: V=4.00 l, P=2.00 atm, t = 27.0o C. Se dilata el gas a presión constante hasta duplicar su volumen. A continuación se comprime isotérmicamente hasta recuperar el volumen inicial. Finalmente se enfría a volumen constante hasta su presión inicial.
- Dibuja el ciclo en un diagrama PV.
- Calcula el trabajo realizado sobre el gas en el ciclo suponiendo que los procesos son cuasiestáticos.
2.2 Proceso isotérmico y adiabático en un gas perfecto
Se comprime un mol de aire en condiciones estándar mediante un proceso isotermo hasta reducir su volumen a la mitad, luego se expande adiabáticamente hasta recuperar su presión inicial. Ambos procesos son cuasiestáticos. Halle
- La temperatura final
- El trabajo total realizado por el gas
- El calor total absorbido por el gas
- La variación de energía interna
2.3 Expansión adiabática no cuasiestática de un gas ideal
4 moles de nitrógeno están a 25 oC y 30 atm. Se pasa bruscamente la presión hasta un valor de 10 atm mediante una expansión adiabática del gas contra una presión exterior constante de 10 atm. El proceso no es cuasiestático. Calcule
- La temperatura final del gas suponiendo que la ecuación de estado de los gases ideales es aplicable a los estados inicial y final.
- La variación de energía interna.
- El trabajo realizado sobre el gas.
- Compare con las mismas magnitudes en un proceso adiabático cuasiestático que expanda el gas hasta la misma presión final de 10 atm.





