Incremento de energía interna y trabajo en proceso isóbaro (F2GIA)

De Laplace

1 Enunciado

Una cantidad fija de $n$ moles de gas ideal sufre una transformación cuasiestática a presión constante $P 0$ , entre el estado inicial $A (V A; T A)$ , y el final $B (V B; T B)$ . ¿Cuál es la variación de energía interna experimentada por el gas en el proceso? ¿Qué cantidad de trabajo se ha transferido al sistema?

2 Solución

Al tratarse de un problema a presión constante, el cálculo del trabajo realizado sobre el sistema es sistema es inmediato:

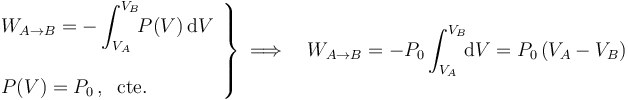
$\left.\begin{array}{l}\displaystyle W_{A\rightarrow B}=-\int_{V_A}^{V_B}\!\! P(V) \!\ \mathrm{d}V\\ \\ \displaystyle P(V)=P_0\,\mathrm{,}\;\;\,\mathrm{cte.}\end{array}\right\}\;\Longrightarrow\quad W_{A\rightarrow B}=-P_0\int_{V_A}^{V_B}\!\! \mathrm{d}V=P_0\!\ (V_A-V_B)$

Al tratarse de un proceso cuasiestático en un gas ideal, en todo momento del proceso se deberá verificar la ley correspondiente a este tipo de sistema termodinámico:

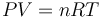
$\displaystyle PV=n R T$

donde $n$ es la cantidad fija de moles. Como dicha ley también se ha de verficar también en los estados inicial y final, se tendrá que,

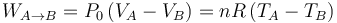
$W_{A\rightarrow B}=P_0\!\ (V_A-V_B)=nR\!\ (T_A-T_B)$

Para determinar la variación de energía interna, aplicamos el primer principio de la termodinámica:

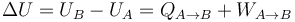
$\Delta U =U_B-U_A=Q_{A\rightarrow B}+W_{A\rightarrow B}$

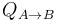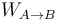donde $U A$ y $U B$ son los valores de la energía interna del gas en los estados inicial y final, respectivamente, y $Q_{A\rightarrow B}$ y $W_{A\rightarrow B}$ las cantidades de calor y trabajo transferidas al sistema. Para calcular el calor transferido utilizamos el concepto de capacidad calorífica del gas a presión constante, $C P$ , que es la cantidad de calor fija absorbida por los $n$ moles de gas para que aumenten su temperatura un kelvin. La capacidad calorífica por mol de sustancia se conoce como calor específico molar, 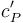$c_P^\prime$ , verificándose,

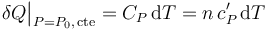
$\delta Q\big|_{P=P_0,\,\mathrm{cte}}=C_P\!\ \mathrm{d}T=n\!\ c_P^\prime\!\ \mathrm{d}T$

El calor específico molar de un gas en condiciones de gas ideal no depende de los valores de las coordenadas termodinámicas; es decir, va a tener un valor fijo que no depende de la temperatura, por lo que el calor transferido al sistema en el proceso bajo estudio será:

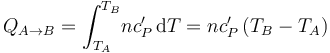
$Q_{A\rightarrow B}=\int_{T_A}^{T_B}\! nc_P^\prime\!\ \mathrm{d}T=nc_P^\prime\!\ (T_B-T_A)$

... y el incremento de energía interna...

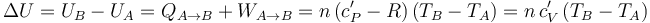
$\Delta U =U_B-U_A=Q_{A\rightarrow B}+W_{A\rightarrow B}=n\!\ (c_P^\prime-R)\!\ (T_B-T_A)=n\!\ c_V^\prime\!\ (T_B-T_A)$

donde se ha aplicado la ley de Mayer para los gases ideales, que establece que en estos sistemas las capacidades caloríficas molares a presión y volumen constante están relacionadas según la expresión

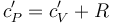
$c_P^\prime=c_V^\prime+R$

Pero podríamos haber seguido otro procedimiento para determinar el incremento de energía interna: el experimento de Joule relativo a la expansión libre de una gas ideal establece que la energía interna de este sistema depende exclusivamente su temperatura. Por tanto, una variación infinitesimal de dicha función de estado deberá ser de la forma,

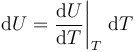
$\,\mathrm{d}U=\frac{\mathrm{d}U}{\mathrm{d}T}\bigg|_{T}\ \mathrm{d}T$

donde la derivada es ha de entenderse como un coeficiente que establece cuánto cambia la energía interna del gas, por unidad de temperatura, en el entorno de un valor $T$ para dicha magnitud. Obsérvese que como la energía interna del gas ideal sólo depende de la temperatura, dicho coeficiente no va a depender ni del volumen ni de la presión del gas y, en consecuencia, ha de ser el mismo, independientemente del tipo de proceso que esté experimentando el sistema. Así que, consideremos un proceso que nos permita determinar fácilmente el valor de dicho coeficiente: en un proceso en que el gas ideal mantenga un volumen consante, $V 0$ , la cantidad de trabajo transferido será nula. Por tanto, según el primer principio de la Termodinámica, la variación de energía intera será exclusivamente debida a la transferencia de calor, la cuál podrá expresarse en términos de la capacidad calorífica/calor específico a volumen constante:

$\left. \begin{array}{l}\displaystyle\delta W\big|_{V=V_0,\,\mathrm{cte}}=-P\,\overbrace{\mathrm{d}V}^{=0}=0\\ \\ \displaystyle \delta Q\big|_{V=V_0,\,\mathrm{cte}}=C_V\!\ \mathrm{d}T=n\!\ c_V^\prime\!\ \mathrm{d}T\end{array}\right\} \quad\Longrightarrow\quad \frac{\mathrm{d}U}{\mathrm{d}T}\bigg|_{T}\ \mathrm{d}T=\mathrm{d}U=[\delta Q+\delta W]_{V=V_0,\,\mathrm{cte}}=n\!\ c_V^\prime\!\ \mathrm{d}T$

Es decir, en cualquier proceso termodinámico de un gas ideal, el incremento de energía interna es proporcional a la variación de temperatura que experimente, siendo la constante de proporcionalidad la capacidad calorífica a volumen constante (o el calor específico a volumen constante multiplicado por la cantidad de sustancia), independientemente de que el proceso se verifique o no a volumen constante. En consecuencia, si en un proceso cualquiera, la temperatura de una cantidad fija de gas ideal varía desde un valor inicial $T A$ hasta un valor final $T B$ , su energía interna sufre un incremento...

$\Delta U=U_B-U_A=\int_{T_A}^{T_B}\! nc_V^\prime\!\ \mathrm{d}T=nc_V^\prime\!\ (T_B-T_A)$

Incremento de energía interna y trabajo en proceso isóbaro (F2GIA)

De Laplace

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES