Entrar Página Discusión Historial Go to the site toolbox

Problemas de cinemática tridimensional de la partícula (GIOI)

De Laplace

Contenido

1 Movimiento circular en el plano OXY

Una partícula se mueve según la ecuación horaria

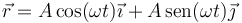
\vec{r}=A \cos⁡(\omega{}t) \vec{\imath}+A\,\mathrm{sen⁡}(\omega{}t)\vec{\jmath}
  1. Determine la trayectoria que sigue la partícula.
  2. Para cada instante t, halle:
    1. La velocidad y la rapidez.
    2. La aceleración.
    3. Las componentes intrínsecas de la aceleración, tanto en forma vectorial como escalar.
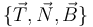
    4. El triedro de Frenet \{\vec{T},\vec{N},\vec{B}\}
    5. El radio y el centro de curvatura

Solución

2 Anilla ensartada en dos varillas

Una pequeña anilla P se encuentra ensartada en la intersección de dos barras giratorias. Los extremos fijos de las barras distan una cantidad 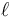\ell y giran en el mismo sentido con la misma velocidad angular de módulo constante Ω de forma que describen los ángulos indicados en la figura:

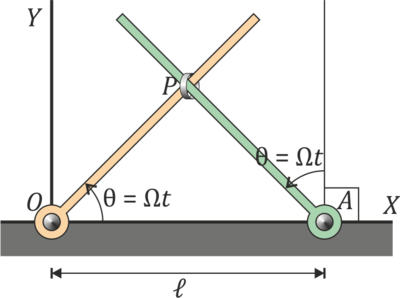
  1. ¿Cuáles son las ecuaciones horarias de P?
  2. ¿Qué clase de trayectoria describe?
  3. ¿Qué tipo de movimiento realiza?

Solución

3 Análisis de ecuación horaria

Una partícula se mueve por el espacio de forma que su velocidad, en las unidades fundamentales del SI, viene dada por la ecuación horaria

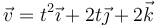
\vec{v}=t^2\vec{\imath}+2t\vec{\jmath}+2\vec{k}

Inicialmente la partícula se encuentra en 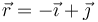\vec{r}=-\vec{\imath}+\vec{\jmath}.

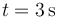  1. Calcule la posición en función del tiempo y el desplazamiento entre t=0\,\mathrm{s} y t=3\,\mathrm{s}. ¿Cuánto vale la velocidad media en dicho intervalo?
  2. Halle la rapidez en cada instante, así como la distancia que recorre la partícula en el mismo intervalo de tiempo. ¿Cuánto vale la rapidez media en este intervalo?
  3. Halle las componentes intrínsecas de la aceleración en t=1\,\mathrm{s}, como escalares y como vectores.
  4. Halle el triedro de Frenet en t=1\,\mathrm{s}.
  5. Calcule el radio de curvatura en t=1\,\mathrm{s} así como el centro de curvatura en ese instante.

Solución

4 Movimiento en un tiro parabólico

Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante

\vec{a}(t)=-g\vec{k}

una posición inicial nula (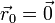\vec{r}_0=\vec{0}) y una velocidad inicial que forma un ángulo α con la horizontal y tiene rapidez inicial v0.

  1. Determine el vector de posición, la velocidad y la aceleración en cada instante.
  2. Halle el punto donde la partícula impacta con el suelo. ¿Cuál es el alcance máximo para una rapidez inicial dada?
  3. Calcule la celeridad y el vector tangente en el instante inicial y en el instante en que se encuentra a mayor altura.
  4. Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los dos instantes anteriores.
  5. Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
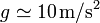  6. Suponga que se quiere alcanzar un blanco situado a 60 m con un mortero que comunica una rapidez inicial de 25 m/s. ¿Con qué ángulo debe dispararse si en medio se encuentra un eucalipto de 15 m de altura? (supóngase g\simeq 10\,\mathrm{m}/\mathrm{s}^2)

Solución

5 Movimiento con aceleración constante

Una partícula se mueve con aceleración constante 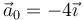\vec{a}_0=-4\vec{\imath} (m/s²), siendo su posición inicial el origen de coordenadas y su velocidad inicial 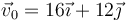\vec{v}_0=16\vec{\imath}+12\vec{\jmath} (m/s).

  1. Halle su posición como función del tiempo.
  2. Determine el instante en que la rapidez o celeridad es mínima. Para este instante halle:
    1. La aceleración tangencial y la normal (escalares)
    2. Los vectores del triedro de Frenet
    3. El radio de curvatura
    4. El centro de curvatura
  3. Calcule en qué instante vuelve a pasar por el eje OY. Para este instante halle:
    1. La posición y la velocidad
    2. Los vectores del triedro de Frenet
    3. La aceleración tangencial y la normal (escalares)

Solución

6 Tiro parabólico sobre una pendiente

Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.

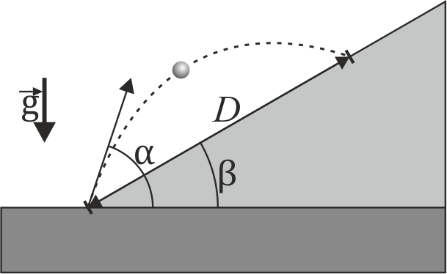
Archivo:parabola-pendiente.png
  1. ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
  2. Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
    1. La rapidez que tiene en el momento del impacto.
    2. La aceleración tangencial y normal (escalares) en el momento de impacto.

Tómese 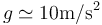g\simeq 10\mathrm{m}/\mathrm{s}^2.

Solución

7 Estudio de un movimiento tridimensional

Una partícula se mueve según las ecuaciones horarias

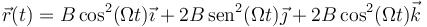
\vec{r}(t)=B\cos^2(\Omega t)\vec{\imath}+2B\,\mathrm{sen}^2(\Omega t)\vec{\jmath}+2B\cos^2(\Omega t)\vec{k}
  1. ¿Qué trayectoria sigue la partícula?
  2. Determine la ley horaria s(t). Suponga que s(0) = 0.
  3. ¿Qué tipo de movimiento describe la partícula?

Solución

8 Velocidad y aceleración en puntos terrestres

La Tierra la podemos modelar como una esfera de 6370 km de radio. Determine la rapidez y la aceleración normal (expresada en unidades de g) para un punto del ecuador terrestre debida al movimiento de rotación terrestre. ¿Cuánto valen la rapidez y aceleración normal en Sevilla (latitud 37°24′40″N)?

Solución

9 Velocidad y aceleración orbital de la Tierra

La órbita terrestre es aproximadamente circular con un radio 1UA = 149.60Gm. ¿Cuánto vale la rapidez y la aceleración normal de la Tierra en su movimiento orbital?

Solución

10 Movimiento circular en 3D

Una partícula se mueve según las ecuaciones horarias

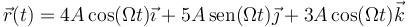
\vec{r}(t)=4A\cos(\Omega t)\vec{\imath}+ 5A\,\mathrm{sen}(\Omega t)\vec{\jmath}+3A\cos(\Omega t)\vec{k}

con A y Ω constantes.

  1. ¿Qué trayectoria sigue la partícula?
  2. ¿Qué desplazamiento realiza y qué distancia recorre la partícula entre t=0 y t = π/Ω?
  3. Justifique que este movimiento es circular y uniforme
  4. Determine la posición del centro del movimiento circular
  5. Calcule la velocidad angular de este movimiento circular

Solución

11 Ejemplo de movimiento expresado en polares

Una partícula describe una curva cuya ecuación en coordenadas polares es

\rho = A\cos(\Omega t)\qquad\qquad \theta = \Omega t
  1. Calcule la velocidad y la aceleración en cada instante.
  2. Halle las componentes intrínsecas de la aceleración para todo t.
  3. Calcule el radio y el centro de curvatura en todo momento.
  4. ¿De qué tipo de movimiento se trata?

Solución

12 Caso de movimiento circular

Una partícula describe un movimiento circular de radio R, tal que su velocidad angular instantánea cumple

\omega = k\theta\,

con k una constante y θ el ángulo que el vector de posición instantánea forma con el eje OX.

  1. Determine la aceleración angular de la partícula como función del ángulo θ.
  2. Halle las componentes intrínsecas de la aceleración lineal en θ = π / 2 y θ = π.
  3. Determine la ley horaria θ = θ(t).

Solución

13 Ejemplo de movimiento helicoidal

El movimiento de un pájaro en una corriente térmica es aproximadamente helicoidal, compuesto de un movimiento ascensional y uno de giro alrededor del eje de subida, de forma que la velocidad en cada punto de la trayectoria puede escribirse como

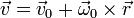
\vec{v}=\vec{v}_0+\vec{\omega}_0\times\vec{r}

siendo

\vec{v}_0 = v_0\vec{k}\qquad \vec{\omega}_0=\omega_0 \vec{k}

dos vectores constantes. Si la posición inicial es 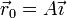\vec{r}_0=A\vec{\imath}

  1. Determine la velocidad en cada punto expresada en la base de coordenadas cilíndricas.
  2. Determine las ecuaciones horarias ρ = ρ(t), θ = θ(t) y z = z(t). ¿Cuánto vale el paso de rosca de la hélice, esto es, lo que sube en el tiempo que da una vuelta alrededor del eje?
  3. Calcule la aceleración del movimiento, así como sus componentes intrínsecas en cada punto del movimiento.
  4. Determine el radio de curvatura de la trayectoria en cualquier instante.

Solución

14 Espiral logarítmica

Una partícula describe una espiral logarítmica a partir de t = 0 de manera que, en el SI y empleando coordenadas polares,

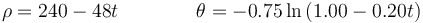
\rho = 240-48t\qquad\qquad \theta = -0.75\ln\left(1.00-0.20t\right)
  1. Halle la velocidad en cada instante.
  2. Calcule la rapidez del movimiento como función del tiempo.
  3. ¿Cuánto tiempo tarda la partícula en llegar al origen de coordenadas? ¿Cuántas vueltas alrededor del origen da en ese tiempo?
  4. Halle la aceleración para cada instante, así como sus componentes intrínsecas
  5. Calcule los vectores tangente y normal a la trayectoria en cada punto de ésta, en función de la base \{\vec{u}_\rho,\vec{u}_\theta\}
  6. Calcule el radio de curvatura como función del tiempo.

Solución

15 Oscilador armónico tridimensional

Una partícula se mueve en tres dimensiones de forma tal que verifica la ecuación del oscilador armónico

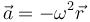
\vec{a}=-\omega^2\vec{r}

con 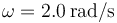\omega = 2.0\,\mathrm{rad}/\mathrm{s}. Su posición inicial es \vec{r}_0=5\,\vec{\imath}\ (\mathrm{m}).

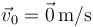  1. Para el caso \vec{v}_0=\vec{0}\,\mathrm{m}/\mathrm{s}. ¿Qué tipo de movimiento describe la partícula?
  2. Para el caso \vec{v}_0=10.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es la trayectoria? ¿Qué tipo de movimiento describe la partícula?
  3. Suponga ahora que \vec{v}_0=8.0\,\vec{\jmath}\,\mathrm{m}/\mathrm{s}, ¿cómo es ahora la trayectoria de la partícula?
  4. Para los tres casos anteriores, determine
  1. la rapidez,
  2. las componentes intrínsecas de la aceleración,
  3. los vectores tangente y normal,
  4. el radio de curvatura y el centro de curvatura.
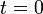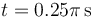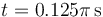para los instantes t=0\,, t=0.25\pi\,\mathrm{s} y t = 0.125\pi\,\mathrm{s}.

Solución

16 Rotación tridimensional de una partícula

Una partícula describe un movimiento circular alrededor del origen de forma que en un cierto instante su posición la da el vector

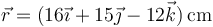
\vec{r}=(16\vec{\imath}+15\vec{\jmath} -12\vec{k})\,\mathrm{cm}

La velocidad angular de la partícula en el mismo instante es

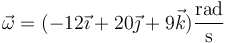
\vec{\omega}=(-12\vec{\imath}+20\vec{\jmath}+9\vec{k})\frac{\mathrm{rad}}{\mathrm{s}}

En el mismo instante la aceleración angular tiene sentido opuesto a la velocidad angular y módulo 0.50 rad/s². Para este instante, calcule:

  1. La velocidad lineal y la rapidez de la partícula.
  2. La aceleración tangencial y la aceleración normal, tanto escalares como vectores.
  3. Los vectores tangente y normal.
  4. El radio de curvatura y el centro de curvatura.

Solución

17 Movimiento circular con aceleraciones relacionadas

Una partícula describe un movimiento circular en el plano XY alrededor del origen de coordenadas de tal forma que en todo instante se cumple la relación entre las componentes intrínsecas escalares de la aceleración:

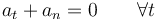
a_t + a_n = 0\qquad \forall t

Inicialmente la partícula se encuentra en 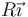R\vec{\imath}, moviéndose con velocidad v_0\vec{\jmath}

  1. Para el instante t = 0, halle el vector aceleración, el vector velocidad angular y el vector aceleración angular.
  2. Calcule la rapidez de la partícula como función del tiempo.
  3. Halle la distancia recorrida, así como el ángulo θ que el vector de posición forma con el eje OX, como función del tiempo

Solución

18 Partícula unida a un sistema articulado

Se tiene un sistema articulado formado por dos barras de la misma masa y la misma longitud h situadas sobre una superficie horizontal. La primera barra tiene un extremo O fijo, de forma que gira alrededor de él con velocidad angular constante Ω respecto a un sistema de ejes fijos OXY. La segunda barra está articulada en el extremo A de la primera y gira respecto de los mismos ejes fijos con una velocidad angular − 2Ω. En el instante t = 0 el sistema está completamente extendido a lo largo del eje OX.

  1. Escriba las ecuaciones horarias de la posición del punto B para todo instante.
  2. Para el instante t = 0 halle
    1. La velocidad y la rapidez.
    2. La aceleración como vector y sus componentes intrínsecas (escalares).
    3. El radio y el centro de curvatura.
  3. Para el instante t = π / (2Ω) calcule
    1. La velocidad y la rapidez.
    2. La aceleración como vector y sus componentes intrínsecas (escalares).

Solución

19 Caso de movimiento con aceleración constante

Una partícula se mueve con aceleración constante, de forma que en tres instantes sucesivos ocupa las siguientes posiciones

t(s) 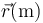\vec{r} (\mathrm{m})
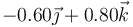
0\, -0.60\vec{\jmath}+0.80\vec{k}
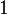
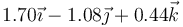
1\, 1.70\vec{\imath}-1.08\vec{\jmath}+0.44\vec{k}
2\, 4.80\vec{\imath}+2.28\vec{\jmath}+2.96\vec{k}
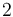
  1. Halle la velocidad media en el intervalo (0 s,2 s)
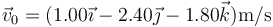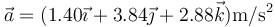
  2. Demuestre que la velocidad instantánea inicial (en t = 0\,\mathrm{s}) y la aceleración del movimiento valen \vec{v}_0=(1.00\vec{\imath}-2.40\vec{\jmath}-1.80\vec{k})\mathrm{m}/\mathrm{s} y \vec{a}=(1.40\vec{\imath}+3.84\vec{\jmath}+2.88\vec{k})\mathrm{m}/\mathrm{s}^2
  3. Para el instante t = 1\,\mathrm{s}, halle:
    1. La velocidad, la rapidez y la aceleración instantáneas
    2. La aceleración tangencial y la aceleración normal (escalares)
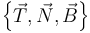
    3. Los vectores del triedro de Frenet \left\{\vec{T},\vec{N},\vec{B}\right\}
    4. El radio de curvatura y el centro de curvatura.

Solución

20 Masa colgando de un hilo

Una partícula se halla situada en el extremo de un hilo de longitud 2b, uno de cuyos extremos se encuentra en el punto A(b,0) y que pasa por una pequeña polea situada en el extremo de una barra de longitud b que gira alrededor del origen O(0,0) con velocidad angular constante 2Ω. En t = 0 la barra está completamente horizontal. La partícula cuelga verticalmente del hilo tras pasar éste por la polea y el movimiento es lo suficientemente lento como para que la partícula no oscile.

  1. Determine la posición, velocidad y aceleración de la partícula como función del tiempo.
  2. Para el instante t = π / (2Ω), halle
    1. La posición, velocidad y aceleración de la partícula.
    2. El triedro de Frenet referido a la base canónica \{\vec{\imath},\vec{\jmath},\vec{k}\}
    3. Las componentes intrínsecas de la aceleración (escalares).
    4. El radio y el centro de curvatura.

Solución

21 Cálculo con valores instantáneos

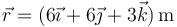En t=0\,\mathrm{s} una partícula se halla en el punto \vec{r}=(6\vec{\imath}+6\vec{\jmath}⃗+3\vec{k})\,\mathrm{m} siendo su velocidad en ese instante 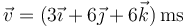\vec{v}=(3\vec{\imath}+6\vec{\jmath}⃗+6\vec{k})\,\mathrm{m}⁄\mathrm{s} y su aceleración 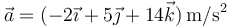\vec{a}=(-2\vec{\imath}+5\vec{\jmath}⃗+14\vec{k})\,\mathrm{m}/\mathrm{s}^2 . En ese instante, ¿la partícula está acelerando o frenando? ¿Dónde está el centro de curvatura en ese momento?

Solución

Obtenido de "http://tesla.us.es/wiki/index.php/Problemas_de_cinem%C3%A1tica_tridimensional_de_la_part%C3%ADcula_(GIOI)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 15:44, 18 nov 2020. - Esta página ha sido visitada 3.398 veces. - Aviso legal - Acerca de Laplace