Análisis de ecuación horaria (GIOI)

De Laplace

Contenido

1 Enunciado
2 Posición y desplazamiento
- 2.1 Posición instantánea
- 2.2 Desplazamiento
3 Rapidez y distancia
- 3.1 Rapidez
- 3.2 Distancia
4 Componentes intrínsecas de la aceleración
- 4.1 Aceleración tangencial
- 4.2 Aceleración normal
5 Triedro de Frenet
6 Radio y centro de curvatura

1 Enunciado

Una partícula se mueve por el espacio de forma que su velocidad, en las unidades fundamentales del SI, viene dada por la ecuación horaria

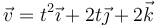
$\vec{v}=t^2\vec{\imath}+2t\vec{\jmath}+2\vec{k}$

Inicialmente la partícula se encuentra en 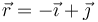$\vec{r}=-\vec{\imath}+\vec{\jmath}$ .

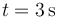Calcule la posición en función del tiempo y el desplazamiento entre $t=0\,\mathrm{s}$ y $t=3\,\mathrm{s}$ . ¿Cuánto vale la velocidad media en dicho intervalo?
Halle la rapidez en cada instante, así como la distancia que recorre la partícula en el mismo intervalo de tiempo. ¿Cuánto vale la rapidez media en este intervalo?
Halle las componentes intrínsecas de la aceleración en $t=1\,\mathrm{s}$ , como escalares y como vectores.
Halle el triedro de Frenet en $t=1\,\mathrm{s}$ .
Calcule el radio de curvatura en $t=1\,\mathrm{s}$ así como el centro de curvatura en ese instante.

2 Posición y desplazamiento

2.1 Posición instantánea

Calculamos la posición instantánea integrando la velocidad

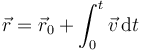
$\vec{r}=\vec{r}_0+\int_0^t\vec{v}\,\mathrm{d}t$

lo que nos da

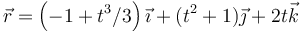
$\vec{r}=\left(-1+t^3/3\right)\vec{\imath}+(t^2+1)\vec{\jmath}+2t\vec{k}$

2.2 Desplazamiento

El desplazamiento lo da la diferencia (vectorial) entre la posición final y la inicial

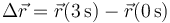
$\Delta \vec{r}=\vec{r}(3\,\mathrm{s})-\vec{r}(0\,\mathrm{s})$

Sustituyendo en la ecuación horaria

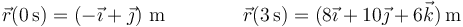
$\vec{r}(0\,\mathrm{s})=\left(-\vec{\imath}+\vec{\jmath}\right)\,\mathrm{m}\qquad\qquad \vec{r}(3\,\mathrm{s})=(8\vec{\imath}+10\vec{\jmath}+6\vec{k})\,\mathrm{m}$

resulta el desplazamiento

$\Delta \vec{r}=\left(9\vec{\imath}+9\vec{\jmath}+6\vec{k}\right)\mathrm{m}$

El módulo de este desplazamiento vale

$\left|\Delta\vec{r}\right|=\sqrt{198}\mathrm{m}=14.1\,\mathrm{m}$

La velocidad media en este intervalo vale

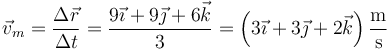
$\vec{v}_m=\frac{\Delta \vec{r}}{\Delta t}=\frac{9\vec{\imath}+9\vec{\jmath}+6\vec{k}}{3}=\left(3\vec{\imath}+3\vec{\jmath}+2\vec{k}\right)\frac{\mathrm{m}}{\mathrm{s}}$

siendo su módulo 4.69&hairsp;m/s.

3 Rapidez y distancia

3.1 Rapidez

Para hallar la distancia recorrida debemos calcular en primer lugar la rapidez, ya que

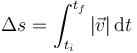
$\Delta s = \int_{t_i}^{t_f}\left|\vec{v}\right|\mathrm{d}t$

Tenemos la velocidad

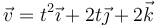
$\vec{v}=t^2\vec{\imath}+2t\vec{\jmath}+2\vec{k}$

Y a partir de esta la rapidez

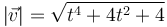
$\left|\vec{v}\right| = \sqrt{t^4+4t^2+4}$

Simplificamos esta expresión si reconocemos en ella un cuadrado de un binomio

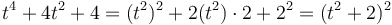
$t^4+4t^2+4 = (t^2)^2 + 2(t^2)\cdot 2 + 2^2 = (t^2+2)^2\,$

y por tanto

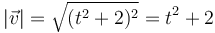
$|\vec{v}|=\sqrt{(t^2+2)^2} =t^2+2$

3.2 Distancia

La distancia recorrida la hallamos integrando la rapidez o celeridad entre el instante inicial y el final

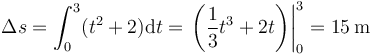
$\Delta s=\int_0^3 (t^2+2)\mathrm{d}t=\left.\left(\frac{1}{3}t^3+2t\right)\right|_0^3 = 15\,\mathrm{m}$

La distancia recorrida es superior al módulo del desplazamiento, ya que la trayectoria es una curva, mientras que el módulo del desplazamiento se mide en línea recta, que siempre es una distancia más corta.

La rapidez media en este intervalo es

$|\vec{v}|_m=\frac{\Delta s}{\Delta t}=5\,\frac{\mathrm{m}}{\mathrm{s}}$

que también es mayor que el módulo de la velocidad media.

4 Componentes intrínsecas de la aceleración

Derivando de nuevo hallamos la aceleración en cada instante

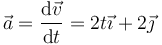
$\vec{a}=\frac{\mathrm{d}\vec{v}}{\mathrm{d}t}=2t\vec{\imath}+2\vec{\jmath}$

En $t=1\,\mathrm{s}$ la velocidad, la rapidez y la aceleración valen

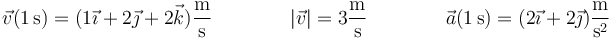
$\vec{v}(1\,\mathrm{s})=(1\vec{\imath}+2\vec{\jmath}+2\vec{k})\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad |\vec{v}| = 3\frac{\mathrm{m}}{\mathrm{s}}\qquad\qquad \vec{a}(1\,\mathrm{s})=(2\vec{\imath}+2\vec{\jmath})\frac{\mathrm{m}}{\mathrm{s}^2}$

4.1 Aceleración tangencial

A partir de ellas podemos calcular la aceleración tangencial proyectando la aceleración sobre la velocidad

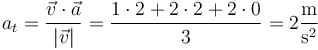
$a_t = \frac{\vec{v}\cdot\vec{a}}{|\vec{v}|}=\frac{1\cdot 2+2\cdot 2+2\cdot 0}{3}=2\frac{\mathrm{m}}{\mathrm{s}^2}$

y, en forma vectorial

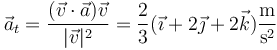
$\vec{a}_t = \frac{(\vec{v}\cdot\vec{a})\vec{v}}{|\vec{v}|^2}= \frac{2}{3}(\vec{\imath}+2\vec{\jmath}+2\vec{k})\frac{\mathrm{m}}{\mathrm{s}^2}$

También podemos hallar la aceleración tangencial derivando la rapidez respecto al tiempo

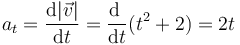
$a_t=\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}=\frac{\mathrm{d}\ }{\mathrm{d}t}(t^2+2) = 2t$

que en $t=1\,\mathrm{s}$ produce el resultado ya conocido

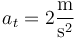
$a_t=2\frac{\mathrm{m}}{\mathrm{s}^2}$

4.2 Aceleración normal

Una vez que tenemos la aceleración completa y la tangencial, podemos hallar la normal restando

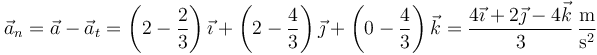
$\vec{a}_n = \vec{a}-\vec{a}_t = \left(2-\frac{2}{3}\right)\vec{\imath}+\left(2-\frac{4}{3}\right)\vec{\jmath}+\left(0-\frac{4}{3}\right)\vec{k}=\frac{4\vec{\imath}+2\vec{\jmath}-4\vec{k}}{3}\,\frac{\mathrm{m}}{\mathrm{s}^2}$

La aceleración normal escalar es el módulo de este vector

$a_n = |\vec{a}_n|= \frac{\sqrt{4^2+2^2+4^2}}{3}=2\,\frac{\mathrm{m}}{\mathrm{s}^2}$

De hecho, operando con las funciones del tiempo, sin sustituir t por 1 s, puede demostrarse que 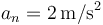$a_n=2\,\mathrm{m}/\mathrm{s}^2$ en todo instante.

La aceleración normal también puede hallarse sin pasar por la aceleración tangencial mediante la fórmula

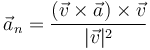
$\vec{a}_n = \frac{(\vec{v}\times\vec{a})\times\vec{v}}{|\vec{v}|^2}$

5 Triedro de Frenet

Ya tenemos dos de los tres vectores que lo forman: el vector tangente

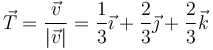
$\vec{T}=\frac{\vec{v}}{|\vec{v}|}=\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}+\frac{2}{3}\vec{k}$

y el vector normal

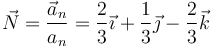
$\vec{N}=\frac{\vec{a}_n}{a_n}=\frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}$

El vector binormal lo hallamos como el producto vectorial de estos dos

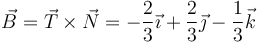
$\vec{B}=\vec{T}\times\vec{N}=-\frac{2}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}-\frac{1}{3}\vec{k}$

Alternativamente, podemos hallar primero el vector binormal a partir de la velocidad y la aceleración

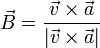
$\vec{B}=\frac{\vec{v}\times\vec{a}}{|\vec{v}\times\vec{a}|}$

y a partir del tangente y del binormal determinar el normal

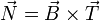
$\vec{N}=\vec{B}\times\vec{T}$

6 Radio y centro de curvatura

El radio de curvatura en el mismo instante lo hallamos a partir de

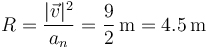
$R=\frac{|\vec{v}|^2}{a_n} = \frac{9}{2}\,\mathrm{m}=4.5\,\mathrm{m}$

Para el centro de curvatura usamos el vector normal, que es el unitario en la dirección de la aceleración normal

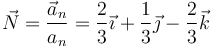
$\vec{N}=\frac{\vec{a}_n}{a_n}=\frac{2}{3}\vec{\imath}+\frac{1}{3}\vec{\jmath}-\frac{2}{3}\vec{k}$

y obtenemos la posición del centro de curvatura como

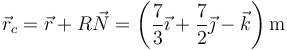
$\vec{r}_c = \vec{r}+R\vec{N}=\left(\frac{7}{3}\vec{\imath}+\frac{7}{2}\vec{\jmath}-\vec{k}\right)\mathrm{m}$

donde hemos usado que

$\vec{r}(1\,\mathrm{s})=\left(-\frac{2}{3}\vec{\imath}+2\vec{\jmath}+2\vec{k}\right)\mathrm{m}$

Análisis de ecuación horaria (GIOI)

De Laplace

Contenido

1 Enunciado

2 Posición y desplazamiento

2.1 Posición instantánea

2.2 Desplazamiento

3 Rapidez y distancia

3.1 Rapidez

3.2 Distancia

4 Componentes intrínsecas de la aceleración

4.1 Aceleración tangencial

4.2 Aceleración normal

5 Triedro de Frenet

6 Radio y centro de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES