Movimiento circular con aceleraciones relacionadas

De Laplace

Contenido

1 Enunciado
2 Vectores en la posición inicial
3 Rapidez como función del tiempo
4 Distancia recorrida

1 Enunciado

Una partícula describe un movimiento circular en el plano XY alrededor del origen de coordenadas de tal forma que en todo instante se cumple la relación entre las componentes intrínsecas escalares de la aceleración:

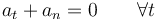
$a_t + a_n = 0\qquad \forall t$

Inicialmente la partícula se encuentra en 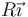$R\vec{\imath}$ , moviéndose con velocidad $v_0\vec{\jmath}$

Para el instante $t = 0$ , halle el vector aceleración, el vector velocidad angular y el vector aceleración angular.
Calcule la rapidez de la partícula como función del tiempo.
Halle la distancia recorrida, así como el ángulo $\varphi$ que el vector de posición forma con el eje OX, como función del tiempo

2 Vectores en la posición inicial

2.1 Aceleración

El vector tangente a la trayectoria es el unitario con dirección y sentido los de la velocidad. En el instante inicial

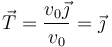
$\vec{T}=\frac{v_0\vec{\jmath}}{v_0}=\vec{\jmath}$

En un movimiento circular, el vector normal es el unitario radial y hacia adentro

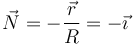
$\vec{N}=-\frac{\vec{r}}{R}=-\vec{\imath}$

La aceleración normal (escalar) en este instante vale

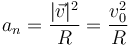
$a_n = \frac{|\vec{v}|^2}{R}=\frac{v_0^2}{R}$

y, por la condición del enunciado

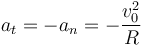
$a_t = -a_n = -\frac{v_0^2}{R}$

Combinando las dos componentes intrínsecas obtenemos el vector aceleración en el instante inicial

$\vec{a}=a_t\vec{T}+a_n\vec{N}=-\frac{v_0^2}{R}\left(\vec{\imath}+\vec{\jmath}\right)$

2.2 Velocidad angular

En un movimiento circular en el plano XY y alrededor del origen, la velocidad y la aceleración angular van en la dirección del eje Z

$\vec{\omega}=\omega\vec{k}\qquad\qquad \vec{\alpha}=\alpha\vec{k}$

cumpliéndose que

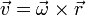
$\vec{v}=\vec{\omega}\times\vec{r}$

Esto nos da

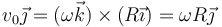
$v_0\vec{\jmath}=(\omega\vec{k})\times(R\vec{\imath})=\omega R\vec{\jmath}$

Igualando y despejando

$\omega=\frac{v_0}{R}\qquad\qquad \vec{\omega}=\frac{v_0}{R}\vec{k}$

2.3 Aceleración angular

En un movimiento circular, la aceleración tangencial (vector) cumple

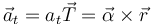
$\vec{a}_t = a_t\vec{T} = \vec{\alpha}\times\vec{r}$

Operando como con la velocidad angular

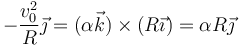
$-\frac{v_0^2}{R}\vec{\jmath}=(\alpha\vec{k})\times(R\vec{\imath})=\alpha R\vec{\jmath}$

lo que nos da

$\alpha=\frac{v_0^2}{R^2}\qquad\qquad \vec{\alpha}=\frac{v_0^2}{R^2}\vec{k}$

3 Rapidez como función del tiempo

La rapidez del movimiento no es una constante, ya que la aceleración tangencial no es nula. En cada instante se cumple

$a_t=\frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t}\qquad\qquad a_n = \frac{|\vec{v}|^2}{R}$

Sustituyendo la condición del enunciado

$a_t = -a_n\qquad\Rightarrow\qquad \frac{\mathrm{d}|\vec{v}|}{\mathrm{d}t} = -\frac{|\vec{v}|^2}{R}$

Llamando, por simplicidad, v a la rapidez, tenemos que resolver la ecuación diferencial

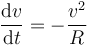
$\frac{\mathrm{d}v}{\mathrm{d}t}=-\frac{v^2}{R}$

Separando los diferenciales

$-\frac{\mathrm{d}v}{v^2}=\frac{\mathrm{d}t}{R}$

Integramos en cada miembro

$-\int_{v_0}^{v}\frac{\mathrm{d}v}{v^2} = \frac{1}{R}\int_0^t\mathrm{d}t$

y queda

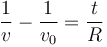
$\frac{1}{v}-\frac{1}{v_0}=\frac{t}{R}$

Despejamos de aquí

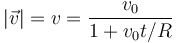
$|\vec{v}| = v = \frac{v_0}{1+v_0 t/R}$

4 Distancia recorrida

La distancia recorrida es la integral de la rapidez

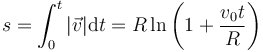
$s = \int_0^t |\vec{v}|\mathrm{d}t = R\ln\left(1+\frac{v_0 t}{R}\right)$

y el ángulo girado es el arco dividido por el radio

$\theta = \ln\left(1+\frac{v_0 t}{R}\right)$

Movimiento circular con aceleraciones relacionadas

De Laplace

Contenido

1 Enunciado

2 Vectores en la posición inicial

2.1 Aceleración

2.2 Velocidad angular

2.3 Aceleración angular

3 Rapidez como función del tiempo

4 Distancia recorrida

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES