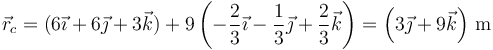Cálculo con valores instantáneos (GIOI)

De Laplace

1 Enunciado

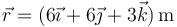En $t=0\,\mathrm{s}$ una partícula se halla en el punto $\vec{r}=(6\vec{\imath}+6\vec{\jmath}⃗+3\vec{k})\,\mathrm{m}$ siendo su velocidad en ese instante 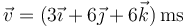$\vec{v}=(3\vec{\imath}+6\vec{\jmath}⃗+6\vec{k})\,\mathrm{m}⁄\mathrm{s}$ y su aceleración 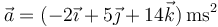$\vec{a}=(-2\vec{\imath}+5\vec{\jmath}⃗+14\vec{k})\,\mathrm{m}⁄\mathrm{s}^2$ . En ese instante, ¿la partícula está acelerando o frenando? ¿Dónde está el centro de curvatura en ese momento?

2 Aceleración

Para saber si frena o acelera, debemos calcular el signo de la aceleración tangencial.

El vector tangente es

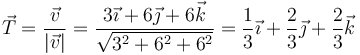
$\vec{T}= \frac{\vec{v}}{|\vec{v}|}=\frac{3\vec{\imath}+6\vec{\jmath}+6\vec{k}}{\sqrt{3^2+6^2+6^2}}=\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}+\frac{2}{3}\vec{k}$

y la aceleración tangencial

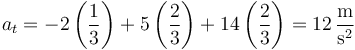
$a_t=-2\left(\frac{1}{3}\right)+5\left(\frac{2}{3}\right)+14\left(\frac{2}{3}\right)=12\,\frac{\mathrm{m}}{\mathrm{s}^2}$

Al ser positiva, la partícula está acelerando.

3 Centro de curvatura

La posición del centro de curvatura es

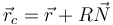
$\vec{r}_c=\vec{r}+R\vec{N}$

siendo

$R=\frac{|\vec{v}|^2}{|\vec{a}_n|}\qquad\qquad \vec{N}=\frac{\vec{a}_n}{|\vec{a}_n|}$

La aceleración normal vale

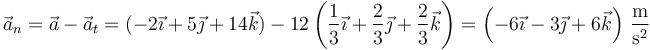
$\vec{a}_n=\vec{a}-\vec{a}_t=(-2\vec{\imath}+5\vec{\jmath}⃗+14\vec{k})-12\left(\frac{1}{3}\vec{\imath}+\frac{2}{3}\vec{\jmath}⃗+\frac{2}{3}\vec{k}\right)=\left(-6\vec{\imath}-3\vec{\jmath}⃗+6\vec{k}\right)\,\frac{\mathrm{m}}{\mathrm{s}^2}$

y su módulo

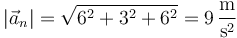
$|\vec{a}_n|=\sqrt{6^2+3^2+6^2}=9\,\frac{\mathrm{m}}{\mathrm{s}^2}$

lo que da

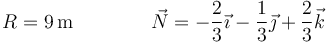
$R=9\,\mathrm{m}\qquad\qquad \vec{N}=-\frac{2}{3}\vec{\imath}-\frac{1}{3}\vec{\jmath}⃗+\frac{2}{3}\vec{k}$

y

$\vec{r}_c=(6\vec{\imath}+6\vec{\jmath}⃗+3\vec{k})+9\left(-\frac{2}{3}\vec{\imath}-\frac{1}{3}\vec{\jmath}⃗+\frac{2}{3}\vec{k}\right)=\left(3\vec{\jmath}+9\vec{k}\right)\,\mathrm{m}$

Cálculo con valores instantáneos (GIOI)

De Laplace

1 Enunciado

2 Aceleración

3 Centro de curvatura

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES