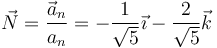Tiro parabólico sobre una pendiente
De Laplace
Contenido |
1 Enunciado
Se desea alcanzar un blanco que se encuentra sobre un plano inclinado un ángulo β, estando el blanco a una distancia D del punto de disparo.
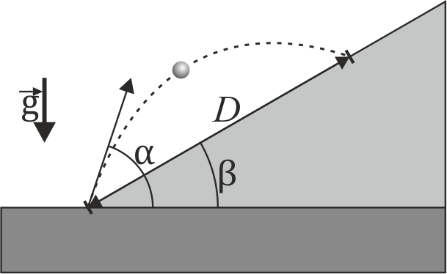
- ¿Cuál es la rapidez mínima que debe tener el proyectil para llegar al blanco? ¿Con qué ángulo sobre la horizontal debe dispararse en ese caso?
- Suponga que el plano tiene una pendiente del 75% y el proyectil se lanza con el ángulo que da el alcance máximo para llegar a D = 100 m. Para este caso, halle:
- La rapidez que tiene en el momento del impacto.
- La aceleración tangencial y normal (escalares) en el momento de impacto.
Tómese 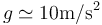 .
.
2 Rapidez mínima
La rápidez de lanzamiento mínima para llegar a un punto es aquella que tiene la distancia al punto como alcance máximo. Si no fuera así, siempre podría reducirse la rapidez de lanzamiento y llegar al mismo punto.
Cuando decimos ¿rapidez mínima respecto a qué? En este problema, los datos son g, la aceleración de la gravedad, β la pendiente del plano y D la distancia al punto de impacto. Lo único que podemos modificar es el ángulo de tiro α, medido respecto a la horizontal.
Variando el ángulo de tiro debemos emplear una rapidez de lanzamiento v0(α) para llegar al blanco. Se tratará entonces de ver para qué valor de α esta rapidez es mínima y cuánto vale este en este caso.
Para obtener esta rapidez hallaremos primero las condiciones para que impacte en un punto cualquiera, para cualquier ángulo de lanzamiento y posteriormente buscaremos el valor que hace mínima la rapidez.
2.1 Alcance general
En el movimiento del proyectil, se cumplen las ecuaciones horarias
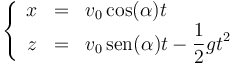
Por otro lado, en el momento de impacto, el proyectil se encuentra sobre la pendiente, por lo que
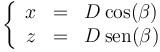
Para hallar el punto de impacto, debemos resolver este sistema de dos ecuaciones con dos incógnitas (t y v0), lo cual se puede hacer de diversas formas. Una vez que hayamos calculado la rapidez de lanzamiento, buscaremos su valor mínimo con respecto al ángulo de lanzamiento.
Primero despejamos el tiempo de impacto
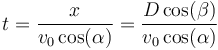
y a continuación sustituimos en la coordenada vertical
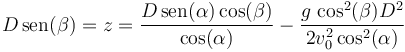
Dividiendo por D en cada miembro obtenemos una ecuación de primer grado y despejando
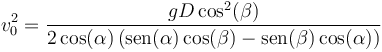
Esta expresión se puede simplificar con ayuda de las relaciones trigonométricas y escribirse como
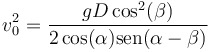
2.2 Rapidez mínima
El procedimiento más “mecánico” para buscar la rapidez mínima consiste en derivar la expresión anterior respecto al ángulo de lanzamiento, igualar a 0 y de ahí obtener el ángulo que da el mínimo. Posteriormente, por sustitución, se halla la rapidez mínima.
Sin embargo, podemos hallar la rapidez mínima sin necesidad de derivar e igualar a cero con ayuda de la relación trigonométrica
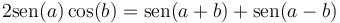
que en este caso da
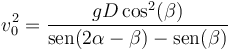
Esta cantidad será mínima cuanto mayor sea el denominador. Dado que β es constante, el mayor denominador se alcanzará cuando

siendo el valor mínimo de la rapidez de lanzamiento al cuadrado
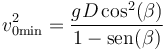
Podemos simplificar la rapidez mínima haciendo uso de otra relación trigonométrica
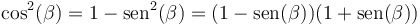
y queda
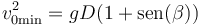
y para la rapidez de lanzamiento
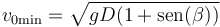
siendo el ángulo de tiro óptimo
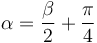
Comprobamos los casos límite conocidos
- Para el plano horizontal β = 0 y resulta el ángulo de máximo alcance y el valor de la rapidez

- Para una pared vertical β = π / 2 y resulta
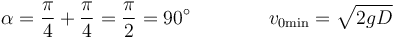
- que quiere decir que, lógicamente, debemos lanzar el proyectil en vertical y el alcance será la máxima altura correspondiente a un tiro vertical
2.3 Velocidad inicial
A partir de la rapidez inicial y del ángulo de lanzamiento
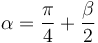
podemos hallar el vector velocidad inicial
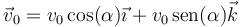
Podemos poner este valor en función de los datos del problema. Por relaciones trigonométricas

lo que da
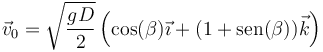
3 Caso particular
3.1 Rapidez de lanzamiento
Si la pendiente es del 75% y la distancia es de 100 m, la rapidez en el momento del lanzamiento debe ser
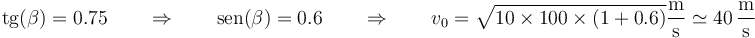
un valor más exacto tomando 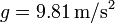 da 39.6m/s.
da 39.6m/s.
La velocidad inicial de lanzamiento, en forma vectorial, es
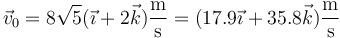
3.2 Rapidez en el impacto
En el caso de un tiro parabolico sobre una superficie horizontal el proyectil impacta con la misma rapidez con la que se disparón. Sobre una pendiente, esto no es cierto.
El cálculo, como en otros problemas, lo podemos realizar utilizando que se trata de un movimiento con aceleración constante. Esto, a su vez, es equivalente a usar la ley de conservación de la energía mecánica.

Multiplicando escalarmente estas dos ecuaciones
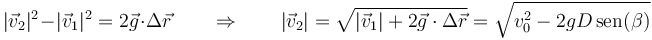
Sustituyendo el valor de la rapidez inicial, queda la de impacto
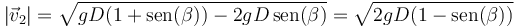
con el valor numérico para el caso particular

Este valor también puede hallarse a partir de las ecuaciones del movimiento uniformente acelerado.
La velocidad en cada instante cumple

con los valores numéricos
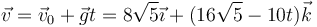
produciéndose el impacto en el momento en que x = Dcos(β)
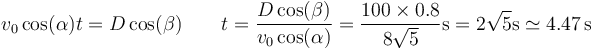
lo que da

con módulo
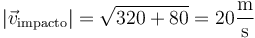
3.3 Componentes de la aceleración
Antes hemos hallado la velocidad en el momento del impacto

por lo que el vector tangente en ese momento es

lo que nos da la aceleración tangencial
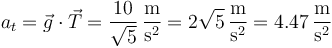
en forma vectorial
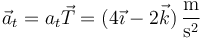
Restando obtenemos la aceleración normal
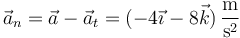
con valor escalar
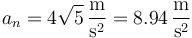
y obtenemos el vector normal a la trayectoria