Problemas de Dinámica del punto (G.I.A.) I: Leyes de la Dinámica. Equilibrio

De Laplace

Contenido 1 Partícula colgando de dos muelles en ángulo recto 2 Asociación de muelles en serie y en paralelo 3 Sistema equivalente a dos resortes alineados 4 Equilibrio de una partícula bajo la acción de tres muelles 5 Equilibrio de una partícula sobre una esfera lisa 6 Equilibrio de una partícula sobre una hélice 7 Muelle en un cuadrilatero 8 Cuerda tirando de una masa 9 Partícula vinculada, en equilibrio y con dos resortes no alineados 10 Equilibrio de partícula y punto sin masa insertados en cuadrilátero vertical 11 Interacciones y aceleraciones en sistema de tres partículas

1 Partícula colgando de dos muelles en ángulo recto

Los resortes AP y BP , tienen longitudes naturales l₁ = 2a y l₂ = 2a, respectivamente, pero se desconoce el valor de sus correspondientes constantes recuperadoras k₁ y k₂. Cada resorte tiene uno de sus extremos conectados a sendos puntos fijos A y B de un plano horizontal, que se hallan separados una distancia de valor 5a. Los extremos libres de los resortes se conectan a una partícula P. La masa de dicha partıcula tiene un valor m tal que el sistema alcanza el equilibrio estático. En dicha situación, se comprueba que las direcciones AP y BP son perpendiculares entre sí y que la AP forma un ángulo θ con la horizontal, tal que su coseno vale 3 / 5.

1. ¿Que relación verifican las constantes recuperadoras de los resortes?
2. Encuentre cuanto vale la masa en función de las constantes de los resortes.

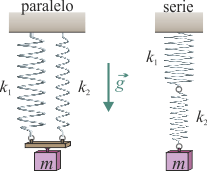
2 Asociación de muelles en serie y en paralelo

Determine constante recuperadora equivalente de un sistema formado por dos muelles de constantes k₁ y k₂ y longitud natural nula, cuando, (a) los muelles están conectados en paralelo y (b) los muelles están conectados en serie.

 

 

 

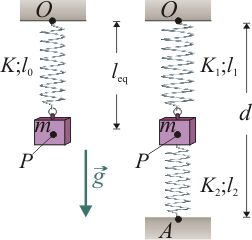
3 Sistema equivalente a dos resortes alineados

Una partícula pesada P de masa m, se halla en equilibrio por la acción de dos resortes, uno de constante recuperadora K₁ y longitud natural l₁, y otro de constante recuperadora K₂ y longitud natural l₂, tales que K₁l₁ = K₂l₂. El primer resorte tiene un extremo conectado a P y el otro a un punto fijo O; el segundo resorte se conecta a la partícula y a un punto fijo A, separado de O por una distancia d. En la situación de equilibrio, los puntos O, P y A están alineados en la dirección y el sentido de (gravedad). ¿Cuáles deben ser los valores de la constante K y la longitud natural l₀ de un único resorte que conectado al punto O, produzca la misma situación de equilibrio que los dos resortes?

 

4 Equilibrio de una partícula bajo la acción de tres muelles

Una partícula libre de masa m está unida a tres muelles de longitud natural nula y constantes elásticas k_A, k_B y k_C. Cada uno de los muelle tiene el otro extremo fijado en un punto. Las coordenadas de los puntos de fijación son A( − a,0,0), B(a,0,0) y C(0,a,0).

1. Calcula la posición de equilibrio de la partícula.
2. Considera las situaciones siguientes
   1. m = 0 y k_A = k_B = k_C = k
   2. m = 0 y
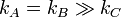
   3. k_A = k_B = k_C = k y m > > ka / g.

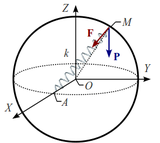
5 Equilibrio de una partícula sobre una esfera lisa

Un punto material M de peso P está obligado a permanecer en la superficie de una esfera de radio R y centro O. Además, M es atraído por un punto fijo A del ecuador de la superficie esférica, debido a la existencia de un resorte elástico ideal, de longitud natural nula y de constante recuperadora 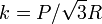, que conecta ambos puntos. Determina las posiciones de equilibrio del punto material M, y la fuerza de reacción vincular en ellas.

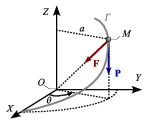
6 Equilibrio de una partícula sobre una hélice

Un punto material M, de peso P, está vinculado a la hélice Γ, definida en el sistema de referencia cartesiano OXYZ por la ecuación vectorial 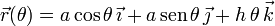. Determina la posición de equilibrio estático del punto M si, además, este es atraído por el origen por una fuerza proporcional a la distancia entre ambos puntos, siendo k la constante de proporcionalidad.

7 Muelle en un cuadrilatero

En el sistema de la figura están marcadas cuatro posibles posiciones de la masa m, sometida a la acción de la gravedad, de un muelle de constante elástica k y longitud natural l₀ y ensartada en el cuadrilátero.

1. Si los vínculos son lisos, ¿cuál de las posiciones de la masa pueden ser de equilibrio?
2. ¿Y si son rugosos?

8 Cuerda tirando de una masa

Un cuerpo de masa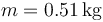 , que puede ser considerado como partícula, se encuentra en contacto con una superficie plana y horizontal –respecto de la vertical gravitatoria–, sobre la que puede deslizar. El contacto entre el cuerpo y la superficie es rugoso, estando caracterizado por un coeficiente estático de rozamiento de valor 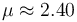. Mediante un cable o similar, se ejerce sobre el cuerpo una fuerza de módulo constante 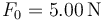, y en la dirección que forma un ́angulo θ = π / 6 con la horizontal. Considérese que el valor de la aceleración de la gravedad es .

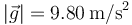1. Dibuje el diagrama de cuerpo libre de la partícula.
2. Si la masa está en equilibrio estático, ¿cuál es el valor del módulo de la fuerza de rozamiento?
3. Manteniendo constante el módulo de la fuerza ejercida por la cuerda, se procede a cambiar su dirección, de manera que el ángulo θ varía dentro del rango 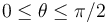. ¿Cuál es el valor límite de dicho ángulo, θ_lim, en que el cuerpo dejaría de estar en reposo y comenzaría a deslizar sobre el plano?

9 Partícula vinculada, en equilibrio y con dos resortes no alineados

El sistema de la figura está formado por dos barras fijas conectadas en el punto O y dirigidas, una en la dirección de la vertical gravitatoria OX, y otra en una dirección horizontal OY. Una partícula pesada P, de masa m, se halla ensartada en la barra vertical, pudiendo deslizar por ella sin rozamiento. Un segundo punto material A, cuya masa es despreciable, está obligado a moverse siempre en la barra horizontal. Un resorte de longitud natural nula y constante recuperadora K₁ tiene conectados cada uno de sus extremos a dichos puntos móviles. Un segundo resorte de constante K₂ y longitud natural l₀ conecta la partícula sin masa A con el punto fijo O. Considerando que el rozamiento entre la barra horizontal y la partícula A es también despreciable, determine las posiciones que ocupan las partículas y las fuerzas de reacción vincular que actúan sobre ellas cuando ambas se encuentran en equilibrio.

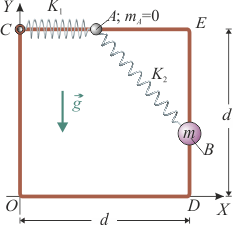
10 Equilibrio de partícula y punto sin masa insertados en cuadrilátero vertical

Cuatro varillas de igual longitud d están dispuestas formando un cuadrado ODEC, contenido en el plano vertical OXY. Un resorte de longitud natural nula y constante recuperadora K₁conecta el vértice fijo C del cuadrilátero con un punto A de masa despreciable que puede desplazarse a lo largo de la varilla horizontal superior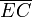 . Además, una partícula material B, cuya masa tiene un valor m está insertada en el lado vertical 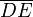de manera que su movimiento está limitado a desplazamientos sobre dicha varilla. Un segundo resorte de longitud natural nula y constante recuperadora K₂ conecta la partícula B al punto A. Los valores de los parámetros del sistema son tales que K₂d > mg.

1. Considerando que los vínculos son perfectamente lisos, determine las posiciones de equilibrio de las partículas A y B.
2. Considérese ahora que, mientras que el vínculo en B sigue siendo liso, la partícula sin masa A está sometida a un vínculo rugoso cuya fuerza de rozamiento verifica las leyes del rozamiento seco. ¿Cuáles son las posiciones de equilibrio?

 

 

11 Interacciones y aceleraciones en sistema de tres partículas

Tres partículas P_O, P₁ y P₂, de masas conocidas con valores m₀, m₁ y m₂, respectivamente, interaccionan entre sí de manera que la fuerza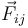 que la partícula P_j ejerce sobre la P_i, tiene la dirección del segmento 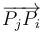(es decir, 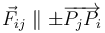). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano OXYZ tal que dicho triángulo está contenido en plano OXY, con el segmento 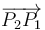paralelo al eje OX, y la partícula P₀ en el punto O. En dicho instante, las aceleraciones de las partículas P₁ y P₂ tiene igual dirección y sentido, siendo paralelas y opuestas al eje OY; es decir 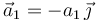y 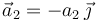, respectivamente, con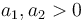

1. Determine qué relación verifican los módulos de dichas aceleraciones, 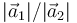, en función de las masas de las partículas.
2. Determine la dirección y el sentido de la aceleración 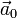de la partícula P₀. ¿Cuánto vale su módulo en relación con los módulos de las aceleraciones de P₁ y P₂?