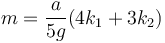F1 GIA PPC 2014, Partícula colgando de dos muelles en ángulo recto
De Laplace
1 Enunciado
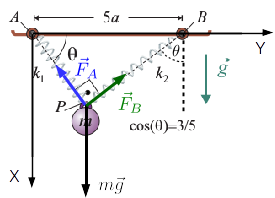
Los resortes AP y BP , tienen longitudes naturales l1 = 2a y l2 = 2a, respectivamente, pero se desconoce el valor de sus correspondientes constantes recuperadoras k1 y k2. Cada resorte tiene uno de sus extremos conectados a sendos puntos fijos A y B de un plano horizontal, que se hallan separados una distancia de valor 5a. Los extremos libres de los resortes se conectan a una partícula P. La masa de dicha partıcula tiene un valor m tal que el sistema alcanza el equilibrio estático. En dicha situación, se comprueba que las direcciones AP y BP son perpendiculares entre sí y que la AP forma un ángulo θ con la horizontal, tal que su coseno vale 3 / 5.
- ¿Que relación verifican las constantes recuperadoras de los resortes?
- Encuentre cuanto vale la masa en función de las constantes de los resortes.
2 Solución
2.1 Fuerzas que actúan sobre la partícula
La partícula está sometida a la acción de tres fuerzas activas: su peso, la del muelle anclado en A y la del muelle anclado en B. Por otro lado, su posición no esta sometida a ninguna restricción, es decir, es libre. Por tanto, no hay fuerzas de reacción vincular. La figura de la derecha indica las fuerzas que actúan sobre la partícula y su dirección.
Vamos a expresar esas fuerzas en función de la posición de la partícula utilizando los ejes indicados en la figura. El peso es
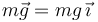
Los muelles tienen longitud natural no nula. Para el muelle anclado en A la fuerza puede calcularse como
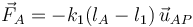
Aquí, lA es la elongación del muelle, y 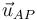 es un vector unitario sobre la recta que une los puntos A y P. La elongación del muelle es la longitud del segmento
es un vector unitario sobre la recta que une los puntos A y P. La elongación del muelle es la longitud del segmento 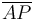 . Del triángulo rectángulo APB obtenemos
. Del triángulo rectángulo APB obtenemos
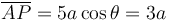
El vector unitario 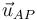 forma un ángulo θ con el eje AY. Su proyección en los ejes es
forma un ángulo θ con el eje AY. Su proyección en los ejes es
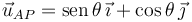
Teniendo en cuenta que l1 = 2a, la fuerza es
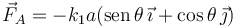
Hacemos lo mismo para el muelle anclado en B. Tenemos
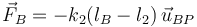
La elongación es
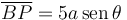
Obtenemos el valor de 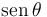 a partir del coseno
a partir del coseno
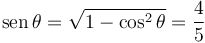
Por tanto
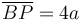
El vector es
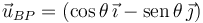
Teniendo en cuenta que el enunciado nos dice que l2 = 3a, la fuerza 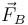 queda
queda
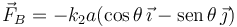
La condición de equilibrio es que la suma de las fuerzas sea cero
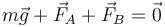
De esta ecuación vectorial obtenemos dos ecuaciones escalares, una por cada componente
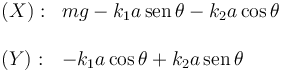
De la segunda ecuación obtenemos
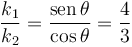
De la otra ecuación obtenemos el valor de la masa