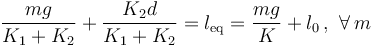Ejercicio de partícula libre en equilibrio, Noviembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado
2 Solución
- 2.1 Sistema de dos resortes
  - 2.1.1 Fuerzas aplicadas
  - 2.1.2 Condición de equilibrio
- 2.2 Sistema equivalente de un resorte

1 Enunciado

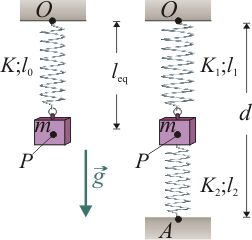
Una partícula pesada

P

de masa

m

, se halla en equilibrio por la acción de dos resortes, uno de constante recuperadora

K 1

y longitud natural

l 1

, y otro de constante recuperadora

K 2

y longitud natural

l 2

, tales que

K 1 l 1 = K 2 l 2

. El primer resorte tiene un extremo conectado a

P

y el otro a un punto fijo

O

; el segundo resorte se conecta a la partícula y a un punto fijo

A

, separado de

O

por una distancia

d

. En la situación de equilibrio, los puntos

O

,

P

y

A

están alineados en la dirección y el sentido de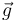 $\vec{g}$ (gravedad). ¿Cuáles deben ser los valores de la constante

K

y la longitud natural

l 0

de un único resorte que conectado al punto

O

, produzca la misma situación de equilibrio que los dos resortes?

2 Solución

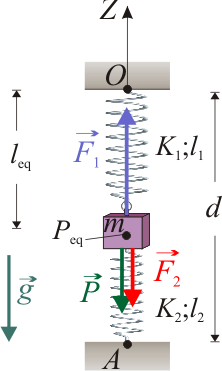
Con el fin de describir analíticamente las magnitudes vectoriales que intervienen en el sistema (fuerzas aplicadas sobre la partícula), definimos un sistema de referencia cuyo eje $O Z$ tenga la dirección de la gravedad y sentido contrario, de manera que 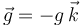$\vec{g}=-g\!\ \vec{k}$ .

2.1 Sistema de dos resortes

2.1.1 Fuerzas aplicadas

Consideremos el cuerpo de masa $m$ como una partícula material $P$ , sometida a la acción de la gravedad y de dos resortes que tienen sus otros extremos conectados a sendos puntos fijos $O$ y $A$ , alineados en la dirección de la vertical gravitatoria. Dichos resortes están caracterizados por sus respectivos valores de constante recuperadora, $K 1$ y $K 2$ , y por los de sus longitudes naturales $l 1$ y $l 2$ . 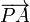Estos resortes ejercen sobre la partícula sendas fuerzas colineales con los segmentos orientados $\overrightarrow{PO}$ y $\overrightarrow{PA}$ , siendo sus magnitudes proporcionales a la elongación de los resortes (es decir, la diferencia entre la longitud total del resorte y su longitud natural); el sentido de las fuerzas debe ser tal que el resorte tienda a recuperar su longitud natural:

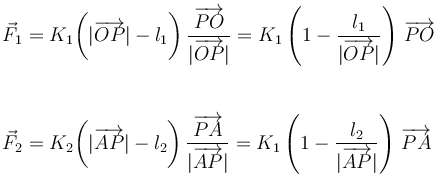
$\begin{array}{l}\displaystyle\vec{F}_1=K_1\bigg(|\overrightarrow{OP}|-l_1\bigg)\!\ \frac{\overrightarrow{PO}}{|\overrightarrow{OP}|}=K_1\left(1-\frac{l_1}{|\overrightarrow{OP}|}\right)\!\ \overrightarrow{PO}\\ \\ \\ \displaystyle\vec{F}_2=K_2\bigg(|\overrightarrow{AP}|-l_2\bigg)\!\ \frac{\overrightarrow{PA}}{|\overrightarrow{AP}|}=K_1\left(1-\frac{l_2}{|\overrightarrow{AP}|}\right)\!\ \overrightarrow{PA} \end{array}$

Sobre la partícula actúa además su peso, que describe la acción de la gravedad:

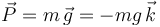
$\vec{P}=m\!\ \vec{g}=-mg\!\ \vec{k}$

2.1.2 Condición de equilibrio

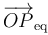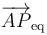Para que el sistema permanezca en una posición de equilibrio, $P eq$ , es condición necesaria que la resultante de todas las fuerzas aplicadas sea nula en todo instante. En el sistema bajo estudio esto implica que los segmentos orientados $\overrightarrow{OP}_\mathrm{eq}$ y $\overrightarrow{AP}_\mathrm{eq}$ deben estar necesariamente alineados con el vector 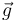$\vec{g}$ (tal como se indica en el enunciado):

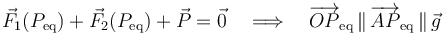
$\vec{F}_1(P_\mathrm{eq})+\vec{F}_2(P_\mathrm{eq})+\vec{P}=\vec{0}\quad\Longrightarrow\quad\overrightarrow{OP}_\mathrm{eq}\!\ \|\!\ \overrightarrow{AP}_\mathrm{eq}\!\ \|\!\ \vec{g}$

o lo que es lo mismo, los puntos $O$ , $A$ y $P eq$ deben estar alineados en la dirección de la vertical gravitatoria (es decir, en la dirección del vector $\vec{k}$ ). Se tendrá, por tanto:

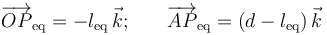
$\overrightarrow{OP}_\mathrm{eq}=-l_\mathrm{eq}\!\ \vec{k}\mathrm{;}\qquad\overrightarrow{AP}_\mathrm{eq}=(d-l_\mathrm{eq})\!\ \vec{k}$

Exigiendo que se verifique la ecuación vectorial que describe la condición de equilibrio, podemos determinar cuál sería la distancia $l eq$ característica de dicho estado:

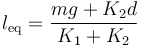
$\vec{F}_1(P_\mathrm{eq})+\vec{F}_2(P_\mathrm{eq})+\vec{P}=\left[K_1(l_\mathrm{eq}-l_1)-K_2(d-l_\mathrm{eq}-l_2)-mg\right]\!\ \vec{k}=\vec{0}$ $\Longleftrightarrow$ $l_\mathrm{eq}=\frac{mg+K_2d}{K_1+K_2}$

donde hemos aplicado la propiedad expresada en el enunciado y que relaciona las constantes recuperadoras y las longitudes naturales de los dos resortes, $K 1 l 1 = K 2 l 2$ .

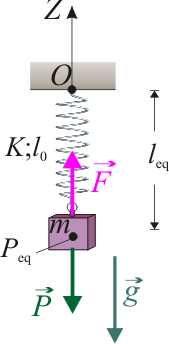
2.2 Sistema equivalente de un resorte

Comparamos ahora con la longitud de equilibrio que se obtendría si hubiésemos utilizado un único resorte de constante recuperadora

K

y longitud natural

l 0

, con su extremo fijo conectado al punto

O

. La fuerza realizada por dicho resorte sería, $\vec{F}=K\bigg(|\overrightarrow{OP}|-l_0\bigg)\!\ \overrightarrow{PO}$

Nuevamente, en la situación de equilibrio los puntos $O$ y $P eq$ han de estar alineados en la dirección de la vertical gravitatoria, y si $l eq$ es la longitud total del resorte, deberá cumplirse:

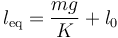
$\vec{F}(P_\mathrm{eq})+\vec{P}=\big[K(l_\mathrm{eq}-l_0)-mg\big]\!\ \vec{k}=\vec{0}$ $\Longleftrightarrow$ $l_\mathrm{eq}=\frac{mg}{K}+l_0$

Este sistema de un sólo resorte será equivalente al de dos resortes si las longitudes de equilibrio $l eq$ en ambos sistemas son las mismas, cualquiera que sea el valor de la masa $m$ . Esto ocurrirá siempre que los parámetros de ambos sistemas (valores de la constantes recuperadoras, longitudes naturales, etc.) veriquen las siguientes relaciones:

$\frac{mg}{K_1+K_2}+\frac{K_2d}{K_1+K_2}=l_\mathrm{eq}=\frac{mg}{K}+l_0\!\ \mathrm{,}\;\;\forall\, m$ $\Longleftrightarrow$ $\begin{array}{l}\displaystyle K=K_1+K_2\\ \\ \displaystyle l_0=\frac{K_2d}{K_1+K_2}\end{array}$

Ejercicio de partícula libre en equilibrio, Noviembre 2012 (F1 GIA)

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Sistema de dos resortes

2.1.1 Fuerzas aplicadas

2.1.2 Condición de equilibrio

2.2 Sistema equivalente de un resorte

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES