Problemas de Movimiento oscilatorio (GIC)
De Laplace
1 Problemas del boletín
1.1 Solución general del MAS
La solución general de la ecuación de movimiento
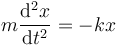
es de la forma
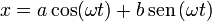
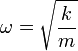
con a y b dos constantes dependientes de las condiciones iniciales.
- Halle el valor de las constantes a y b si la posición inicial de la partícula es x0 y su velocidad inicial es v0.
- Demuestre que la ecuación horaria
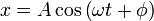 es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
es también solución de la misma ecuación de movimiento. Empleando relaciones trigonométricas, deduzca la relación entre las constantes {A,φ} y las constantes {a,b}. Exprese A y φ en función de la posición y la velocidad iniciales, x0 y v0.
- Calcule la velocidad de la partícula para cualquier instante en función de la posición y velocidad iniciales.
- Demuestre que la cantidad E = mv2 / 2 + kx2 / 2 no depende del tiempo. ¿Cuánto vale en función de las condiciones iniciales?
- Demuestre que x = ejωt, con
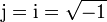 , la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
, la unidad imaginaria, es una solución particular de la ecuación de movimiento. Aplicando los resultados anteriores, demuestre la relación
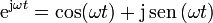
1.2 Masa de un astronauta
Para medir la masa de un astronauta en ausencia de gravedad se emplea un aparato medidor de masa corporal. Este aparato consiste, básicamente, en una silla que oscila en contacto con un resorte. El astronauta ha de medir su periodo de oscilación en la silla. En la segunda misión Skylab el resorte empleado tenía una constante k = 605.6 N/m y el periodo de oscilación de la silla vacía era de 0.90149 s. Calcule la masa de la silla. Con un astronauta en la silla el periodo medido fue 2.08832 s. Calcule la masa del astronauta.
1.3 Barra oscilando respecto a uno de sus extremos
Una barra homogénea de longitud L y masa M cuelga por uno de sus extremos de modo que se encuentra en equilibio en posición vertical. Analiza el movimiento de la barra si se separa de la vertical un ángulo θ0 pequeño.
1.4 Oscilador amortiguado
Un oscilador amortiguado experimenta una fuerza de rozamiento viscoso 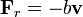 , de forma que su ecuación de movimiento, para un movimiento unidimensional es
, de forma que su ecuación de movimiento, para un movimiento unidimensional es
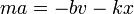
- Demuestre que la energía mecánica
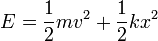
- Si buscamos una solución particular de la forma x = Aeλt, calcule los dos valores que puede tener λ. La solución general será una combinación de las dos posibilidades:
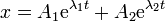
- ¿Cuál es el máximo valor de b para que haya oscilaciones? ¿cómo es el movimiento si b supera ese valor?
- Considere el caso particular de una partícula de masa m = 1 kg se encuentra sujeta a un muelle de constante k =1 N/m, existiendo un rozamiento b. Determine la posición en cualquier instante si se impulsa desde la posición de equilibrio con velocidad v0 = 0.6 m/s si (a) b = 1.6 N·s/m, (b) b = 2.5 N·s/m, (c) b = 2.0 N·s/m.
1.5 Muelle forzado
Una pesa de 1.50 kg está suspendida de un muelle con una constante elástica 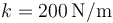 . Una fuerza sinusoidal con una magnitud de 50.0 N excita el sistema. El factor de rozamiento es
. Una fuerza sinusoidal con una magnitud de 50.0 N excita el sistema. El factor de rozamiento es 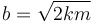 ¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
¿Que frecuencia debe tener la fuerza externa para que el objeto vibre con una amplitud de 0.122 m?
1.6 Calcetín oscilante
Un calcetín colgado para recibir un regalo de Navidad mide 128 mm de largo. El único regalo dentro del calcetín es un teléfono móvil. La persona que ha comprado el móvil llama al número del mismo cuando el destinatario del regalo va a recogerlo. Este observa asombrado que el calcetín ́oscila con una amplitud apreciable. ¿Cuál es el valor aproximado de la frecuencia a la que vibra el móvil? (El móvil tiene conectado el vibrador)
2 Otros problemas
2.1 Pelota que bota y bota
Un balón que se ha dejado caer desde una altura de 4 m choca con el suelo con una colisión perfectamente elástica. Suponiendo que no se pierde energía debido a la resistencia del aire, demuestre que el movimiento es periódico. Determine el periodo del movimiento, ¿Es éste un movimiento armónico simple?
2.2 Oscilador armónico bidimensional
Una partícula de masa m se encuentra sobre una mesa, unida a un punto fijo de ésta (que tomaremos como origen de coordenadas) mediante un muelle de constante k. En el instante t = 0 se la sitúa en la posición 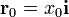 y se le comunica una velocidad
y se le comunica una velocidad 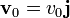 .
.
- Halle la posición de la partícula en cualquier instante.
- ¿Cómo es la trayectoria de la partícula?
- Demuestre que, en este movimiento, las cantidades
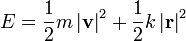
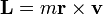
- son constantes de movimiento.
2.3 Asociaciones de resortes
Determine la frecuencia de oscilación de una masa m unida a dos muelles de constantes k1 y k2 cuando
- los muelles están conectados en paralelo.
- los muelles están conectados en serie.
2.4 Masa que cuelga de dos muelles
Se tiene una masa m que cuelga de una asociación de dos muelles en paralelo con constantes recuperadoras k1 y k2 y longitudes naturales L1 y L2, respectivamente.
- Determine el valor de la elongación de la asociación en la situación de equilibrio.
- Se empuja la masa verticalmente hacia arriba con una velocidad inicial v0. Suponiendo que el rozamiento es despreciable, encuentre la evolución de la posición de la masa en el tiempo y el período de oscilación (Escoja como origen de coordenadas la posición de equilibrio del apartado anterior). Calcule la posición más alta que alcanza la masa y su energía en ese instante.
- Se añade un pistón de masa despreciable, de modo que se mueve dentro de un cilindro relleno con nitrógeno. Determine la longitud de onda de la onda de sonido generada en el cilindro, considerando que el gas es ideal.
- Determine los valores numÚricos de las magnitudes pedidas en los apartados anteriores.
Datos: 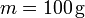 ,
, 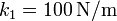 ,
, 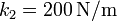 ,
,
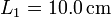 ,
, 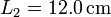 ,
, 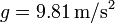 ,
, 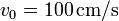 ,
, 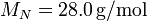 ,
, 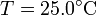
2.5 Error en el péndulo
Halle el error relativo cometido al calcular la velocidad para un péndulo en su punto más bajo empleando la aproximación de oscilador armónico, si se suelta en reposo desde un ángulo respecto a la vertical de (a) 1° (b) 10° (c) 30° (d) 60° (e) 90°.
2.6 Balanza de frutero
Una balanza de frutero cuelga verticalmente de forma que cuándo sólo está el plato, de masa 200 g, la elongación respecto de la elongación natural es de 1.00 cm. De pronto, el frutero suelta 1.00 kg de plátanos en el plato. Despreciando el rozamiento,
- ¿Cuál es la amplitud de las oscilaciones resultantes?
- Cuál es su período?
- ¿Cuál es la velocidad máxima de los plátanos?
- ¿Cuánto vale la energía mecánica del sistema si tomamos como referencia de alturas la posición inicial del plato?
- Supón que, estando en el punto más bajo de sus oscilaciones, uno de los plátanos (de 100 g de masa) cae del plato. ¿Cuál es la amplitud de las oscilaciones que hace el plato a partir de ese momento?
2.7 Partícula en un cuenco
Una partícula de masa m se desliza sin rozamiento dentro de un recipiente de forma hemisférica de radio R. Demuestre que el movimiento de la partícula sobre el cuenco es equivalente a un péndulo de longitud R.
2.8 Oscilador no lineal
Una partícula está sometida exclusivamente a una fuerza, dependiente de la posición, dada por
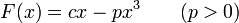
- Halle la expresión de la energía potencial y la energía mecánica para la partícula. Esboce las gráficas para los casos c < 0 y c > 0.
- Demuestre que el movimiento de la partícula siempre es acotado, y periódico.
- Localice las posiciones de equilibrio de la partícula (a) si c < 0 (b) si c > 0.
- Suponga que la partícula se suelta desde una posición muy próxima a las posiciones de equilibrio calculadas en el apartado anterior. ¿En qué caso describe oscilaciones? Halle el valor aproximado del periodo de oscilación para este movimiento.
2.9 Resorte forzado
Un niño juega con un resorte de constante k = 20 N/m y fricción despreciable del cual cuelga una masa m = 200 g, sujetando el otro extremo del resorte entre sus dedos, con la mano extendida horizontalmente. El niño agita la mano arriba y abajo, con una amplitud b = 2 cm y una frecuencia ω. Determine la posición de la pesa, si esta oscila con la misma frecuencia que la mano. ¿En qué condiciones la pesa llegará a golpearle la mano?
2.10 Oscilaciones en un circuito
Un circuito formado por una resistencia R, un condensador C y una autoinducción L, asociadas en serie cumple las siguientes ecuaciones para la carga en el condensador y la corriente en el circuito:
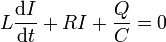
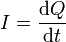
- Suponga en primer lugar que la resistencia es nula (R = 0). Pruebe que la carga del condensador oscila armónicamente. ¿Cuál es la frecuencia de oscilación? ¿Qué energía se conserva, análogamente a la energía mecánica de un oscilador armónico?
- Si la resistencia no es nula, pruebe que el sistema se comporta como un oscilador amortiguado. ¿Cuál es la resistencia máxima para que haya oscilaciones en el sistema?
- Suponga que además de los elementos anteriores, el circuito dispone de una fuente de corriente alterna, que lleva mucho tiempo conectada, de manera que las ecuaciones del circuito son
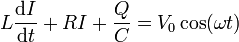
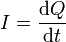
- Halle la amplitud de las oscilaciones de la carga del condensador, como función de los parámetros del circuito y de la frecuencia y amplitud del voltaje aplicado.
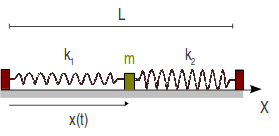
2.11 Partícula sometida a la acción de dos muelles colineales
Se tiene el sistema de la figura, formado por dos muelles de longitud natural nula y constantes elásticas k1 y k2 . Los puntos de anclaje de los muelles están separados por una distancia L. Una partícula de masa m está conectada a los dos muelles y se mueve bajo la acción de éstos. El rozamiento con la superficie es despreciable. Los valores numéricos de los parámetros del problema son
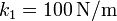 ,
, 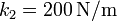 ,
, 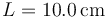 ,
, 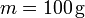 .
.
- Calcula la posición de equilibrio de la partícula.
- Calcula la energía potencial elástica de la partícula cuando está en su posición de equilibrio.
- Estando la partícula en la posición de equilibrio, se le da un empujón hacia la derecha de modo que su velocidad inicial es v0. ¿Cuál es el período de las oscilaciones de la partícula?
- Si el valor numérico de la velocidad inicial es
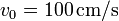 , ¿cuál es la amplitud de las oscilaciones de la partícula?
, ¿cuál es la amplitud de las oscilaciones de la partícula?