Balanza de frutero

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una balanza de frutero cuelga verticalmente de forma que cuándo sólo está el plato, de masa 200 g, la elongación respecto de la elongación natural es de 1.00 cm. De pronto, el frutero suelta 1.00 kg de plátanos en el plato. Despreciando el rozamiento,

¿Cuál es la amplitud de las oscilaciones resultantes?
Cuál es su período?
¿Cuál es la velocidad máxima de los plátanos?
¿Cuánto vale la energía mecánica del sistema si tomamos como referencia de alturas la posición inicial del plato?
Supón que, estando en el punto más bajo de sus oscilaciones, uno de los plátanos (de 100 g de masa) cae del plato. ¿Cuál es la amplitud de las oscilaciones que hace el plato a partir de ese momento?

2 Solución

2.1 Constante del resorte

Cuando sólo está colgando el plato vacío (masa 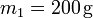$m_1=200\,\mathrm{g}$ ), las fuerzas sobre éste son su peso y la fuerza del resorte. Siguiendo la figura, escogemos el eje $X$ apuntando hacia abajo, de modo que el origen está en el punto de anclaje del muelle. Cuando no está el plato, el extremo del muelle está en $x 0$ (la elongación natural). Al colgar el plato, la posición de equilibrio se obtiene cuando la fuerza del muelle equilibra el peso del plato

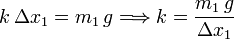
$k\,\Delta x_1 = m_1\,g \Longrightarrow k = \dfrac{m_1\,g}{\Delta x_1}$

La elongación respecto a la elongación natural es

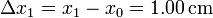
$\Delta x_1 = x_1 - x_0 = 1.00\,\mathrm{cm}$

por lo que la constante del muelle es

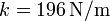
$k = 196\,\mathrm{N/m}$

2.2 Amplitud de las oscilaciones

Las oscilaciones del muelle vienen dadas por la expresión

$s (t) = A cos(ω t + φ)$

donde $s (t)$ es la posición del plato respecto de la posición de equilibrio. Las constantes $A$ y $φ$ se determinan a partir de las condiciones iniciales.

Al añadir los plátanos, de masa 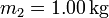$m_2 = 1.00\,\mathrm{kg}$ , la posición de equilibrio cambia. En esa nueva posición de equilibrio el resorte debe compensar el peso de del plato y los plátanos. La elongación de equilibrio respecto a la elongación natural se obtiene de

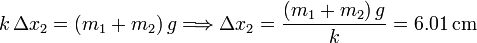
$k\,\Delta x_2 = (m_1 + m_2)\,g \Longrightarrow \Delta x_2 = \dfrac{(m_1+m_2)\,g}{k} = 6.01\,\mathrm{cm}$

donde $Δ x 2 = x 2 - x 0$ .

Justo al añadir los plátanos, el plato está más alto que la nueva posición de equilibrio. Así pues, el valor inicial de $s (t)$ es

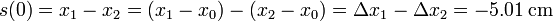
$s(0) = x_1 - x_2 = (x_1-x_0) - (x_2-x_0) = \Delta x_1 - \Delta x_2 = -5.01\,\mathrm{cm}$

La velocidad inicial es cero, pues parte del reposo.

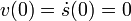
$v(0) = \dot{s}(0) = 0$

Ahora podemos determinar las constantes $A$ y $φ$

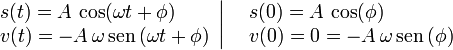
$\begin{array}{cc} \left. \begin{array}{l} s(t) = A\,\cos(\omega t + \phi)\\ v(t) = -A\,\omega\,\mathrm{sen}\,(\omega t + \phi) \end{array} \right|& \begin{array}{l} s(0) = A\,\cos(\phi)\\ v(0)=0=-A\,\omega\,\mathrm{sen}\,(\phi) \end{array} \end{array}$

De la segunda ecuación obtenemos que $φ = 0$ o $φ = π$ . Como $s (0) < 0$ escogemos $φ = π$ , de modo que la amplitud $A$ sea positiva. Tenemos entonces

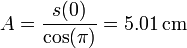
$A = \dfrac{s(0)}{\cos(\pi)} = 5.01\,\mathrm{cm}$

La posición en cada instante del plato es

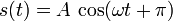
$s(t) = A\,\cos(\omega t + \pi)$

con

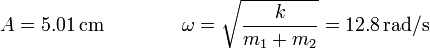
$A = 5.01\,\mathrm{cm}\qquad\qquad \omega = \sqrt{\dfrac{k}{m_1+m_2}} = 12.8\,\mathrm{rad/s}$

2.3 Período

El período de oscilación es

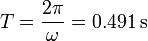
$T = \dfrac{2\pi}{\omega} = 0.491\,\mathrm{s}$

La frecuencia es

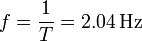
$f = \dfrac{1}{T} = 2.04\,\mathrm{Hz}$

2.4 Velocidad máxima

La velocidad en cada instante es

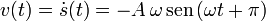
$v(t) = \dot{s}(t) = -A\,\omega\,\mathrm{sen}\,(\omega t + \pi)$

El valor máximo de la velocidad es

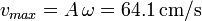
$v_{max} = A\,\omega = 64.1\,\mathrm{cm/s}$

2.5 Energía mecánica

La energía mecánica es la suma de las energías cinética, potencial gravitatoria y potencial elástica. En la posición inicial, cuando $x = x 1$ , escogemos el origen de energía potencial gravitatoria. En esa posición la velocidad es cero (se acaban de poner los plátanos). Por tanto la única energía distinta de cero es la del muelle. Tenemos

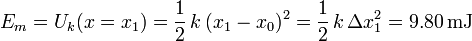
$E_m = U_k (x=x_1) = \dfrac{1}{2}\,k\,(x_1-x_0)^2 = \dfrac{1}{2}\,k\,\Delta x_1^2 = 9.80\,\mathrm{mJ}$

Aplicando la conservación de energía mecánica también puede obtenerse la amplitud de la oscilación. Cuando el plato está en su punto más bajo, su posición es

$x m a x = x 2 + A$

En ese instante, la velocidad es cero, y las energías potenciales son ( $m T = m 1 + m 2$ )

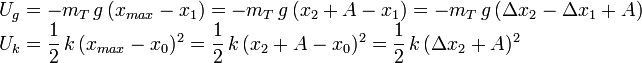
$\begin{array}{l} U_g = -m_T\,g\,(x_{max}-x_1) = -m_T\,g\,(x_2+A-x_1) = -m_T\,g\,(\Delta x_2- \Delta x_1 +A)\\ U_k = \dfrac{1}{2}\,k\,(x_{max}-x_0)^2=\dfrac{1}{2}\,k\,(x_2+A-x_0)^2=\dfrac{1}{2}\,k\,(\Delta x_2+A)^2 \end{array}$

La suma de esas dos energías debe ser igual a la energía mecánica total. Así se obtiene una ecuación para $A$ . Aplicando que 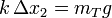$k\,\Delta x_2=m_Tg$ , se obtiene de nuevo el valor de la amplitud (en valor absoluto)

2.6 Se cae un plátano

Al caerse el plátano (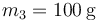 $m_3=100\,\mathrm{g}$ ), cambia otra vez el punto de equilibrio. Ahora corresponde a un punto de coordenada $m 3$ dada por

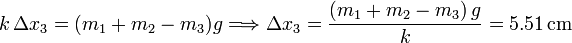
$k\,\Delta x_3 = (m_1+m_2-m_3)g \Longrightarrow \Delta x_3 = \dfrac{(m_1+m_2-m_3)\,g}{k} = 5.51\,\mathrm{cm}$

siendo $Δ x 3 = x 3 - x 0$ .

En el instante en que se cae el plátano la velocidad es cero. Entonces de nuevo la amplitud de las oscilaciones es la distancia desde la posición del plato cuando se cae el plátano hasta la nueva posición de equilibrio. Esta posición era la $x m a x$ del apartado anterior. Entonces

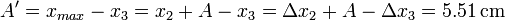
$A' = x_{max} - x_3 = x_2 + A - x_3 = \Delta x_2 + A - \Delta x_3 = 5.51\,\mathrm{cm}$

Esta amplitud es mayor que la anterior, pues ahora el nuevo punto de equilibrio está más arriba.

Balanza de frutero

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Constante del resorte

2.2 Amplitud de las oscilaciones

2.3 Período

2.4 Velocidad máxima

2.5 Energía mecánica

2.6 Se cae un plátano

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES