Oscilador no lineal

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Una partícula está sometida exclusivamente a una fuerza, dependiente de la posición, dada por

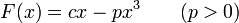
$F(x) = cx - px^3\qquad (p>0)$

Halle la expresión de la energía potencial y la energía mecánica para la partícula. Esboce las gráficas para los casos $c < 0$ y $c > 0$ .
Demuestre que el movimiento de la partícula siempre es acotado, y periódico.
Localice las posiciones de equilibrio de la partícula (a) si $c < 0$ (b) si $c > 0$ .
Suponga que la partícula se suelta desde una posición muy próxima a las posiciones de equilibrio calculadas en el apartado anterior. ¿En qué caso describe oscilaciones? Halle el valor aproximado del periodo de oscilación para este movimiento.

2 Solución

2.1 Energía mecánica

2.1.1 Energía potencial

Esta fuerza, dependiente solo de la posición, es una fuerza conservativa, que deriva de una energía potencial. Podemos calcular esta energía observando que el trabajo realizado por esta fuerza corresponde a una disminución de la energía potencial

$W = -\Delta U\,$ $\int_0^z F(x)\,\mathrm{d}x = -\left(U(z)-U(0)\right)$

Hallando la integral obtenemos la energía potencial

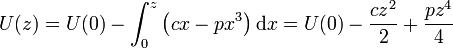
$U(z) = U(0) - \int_0^z \left(cx-px^3\right)\mathrm{d}x = U(0) -\frac{cz^2}{2}+\frac{pz^4}{4}$

Si tomamos como origen de energía potencial el centro del sistema ( $z = 0$ ) nos queda finalmente (llamando $x$ a la variable):

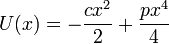
$U(x) = -\frac{cx^2}{2}+\frac{px^4}{4}$

La curva para esta energía potencial tiene las siguientes propiedades:

Es una función par. Puesto que solo aparecen potencias pares, la gráfica de $U (x)$ es simétrica, esto es

U ( - x) = U (x)

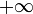Tiende a $+\infty$ para $|x|\to\infty$ . Cuando x es grande, el término en $x 4$ domina sobre $x 2$ (por ejemplo, para $x = 1000$ , $x 2$ es 1 millón y $x 4$ es 1 billón. Esto quiere decir que si nos alejamos lo suficiente de la posición central la energía potencial va creciendo progresivamente.

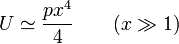
$U\simeq \frac{px^4}{4}\qquad (x\gg 1)$

Puesto que la energía mecánica de una partícula es una cantidad finita, esta propiedad implicará, como veremos, que el movimiento debe ser periódico.

Puede tener un máximo o un mínimo en $x = 0$ . Cuando x es pequeño, $x 2$ es mucho más grande que $x 4$ (para $x$ una décima, $x 2$ es sólo una centésima, pero $x 4$ es aun menor, una diezmilésima). Por ello, cerca del punto central

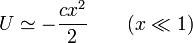
$U\simeq -\frac{cx^2}{2}\qquad (x\ll 1)$

Si

c < 0

, la curva es aproximadamente una parábola hacia arriba, y el punto central es un mínimo (la segunda derivada es positiva). Si

c > 0

, la parábola es hacia abajoy la curva posee un máximo. En combinación con la propiedad anterior, esto significa que habrá dos mínimos adicionales, uno a cada lado.

2.1.2 Energía mecánica

La energía mecánica es la suma de la energía cinética y de la potencial que acabamos de calcular

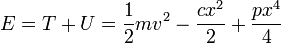
$E = T + U = \frac{1}{2}mv^2 - \frac{cx^2}{2}+\frac{px^4}{4}$

2.2 Movimiento periódico

Se trata de demostrar que el movimiento de una partícula sometida a la fuerza del enunciado (cuya solución no conocemos), es necesariamente periódico. Podemos probar esta afirmación empleando razonamientos energéticos

La energía mecánica es una constante de movimiento, por ser la fuerza conservativa

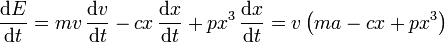
$\frac{\mathrm{d}E}{\mathrm{d}t}= mv\,\frac{\mathrm{d}v}{\mathrm{d}t}-cx\,\frac{\mathrm{d}x}{\mathrm{d}t}+px^3\,\frac{\mathrm{d}x}{\mathrm{d}t}= v\left(ma-cx+px^3\right)$

y, puesto que por la segunda ley de Newton

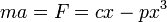
$ma = F = cx - p x^3\,$

esta derivada se anula y

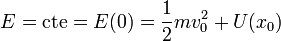
$E = \mathrm{cte} = E(0) = \frac{1}{2}mv_0^2+U(x_0)$

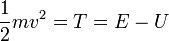
Podemos representar esto gráficamente, con ayuda de la curva de la energía potencial. La constancia de la energía mecánica equivale a una recta horizontal. La energía potencial es la curva de cuarto grado que ya conocemos. La energía cinética es la diferencia entre la energía total y la potencial $\frac{1}{2}mv^2 = T = E -U$

lo que corresponde al segmento verde entre la recta y la curva.

Ahora bien, la energía cinética es siempre positiva (es proporcional a un cuadrado), por tanto, los valores de x deben estar confinados entre los dos puntos de corte de la recta y la curva. Más allá la energía total sería menor que la potencial y la energía cinética sería negativa (lo que es imposible).

Tenemos entonces dos puntos de retorno, en los cuales la partícula se para (puesto que la energía cinética se hace cero). Aunque la partícula, al llegar a esa posición se detiene instantáneamente, no se queda detenida indefinidamente, sino que retrocede (como si rebotara, de ahí lo de retorno), ya que la fuerza está tirando de ella hacia adentro (la velocidad se anula, pero la fuerza no). La partícula se mueve en sentido contrario, hasta que llega al segundo punto de retorno, rebota de nuevo y continúa el proceso. El movimiento se dice acotado, pues alcanza un valor mínimo y un valor máximo de $x$ .

Cada vez que llega al mismo punto de retorno, la partícula se encuentra en la misma posición (la de este punto) y con la misma velocidad (nula), por lo que el movimiento se repite exactamente igual cada vez, y no es solo acotado, sino además periódico.

2.3 Puntos de equilibrio

Los puntos de equilibrio son aquellos en que la fuerza sobre la partícula se anula, y por tanto en ellos la partícula puede permanecer en reposo. Estos puntos corresponderán, a su vez, a los extremos (máximos o mínimos) de la energía potencial (ya que $F = d U / d x$ ).

Haciendo $F = 0$ queda

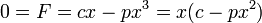
$0 = F = cx-px^3 = x(c-px^2)\,$

Tenemos que una posición de equilibrio es siempre

$x=0\,$

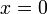
Dependiendo del signo de $c$ (ya que $p > 0$ siempre) tenemos dos casos:

Si 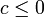$c \leq 0$ no hay más posiciones de equilibrio, ya que el segundo factor es siempre negativo. En este caso, la energía potencial posee un mínimo en $x = 0$ .

Si $c > 0$ existen dos posiciones adicionales de equilibrio, dadas por

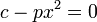
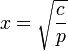
$c - px^2 = 0\,$ $\Rightarrow$ $x = \sqrt{\frac{c}{p}}$

En este caso, la energía potencial posee un máximo en

x = 0

, y los dos mínimos están situados simétricamente.

2.4 Pequeñas oscilaciones

La idea de considerar una posición $x$ próxima a una dada $x 0$ , es que, si $x - x 0$ es pequeño, podemos usar la serie de Taylor en torno a dicha posición. La idea es quedarnos sólo con los términos más pequeños, de forma que en lugar de tratar con una función complicada, empleemos una más sencilla (aunque aproximada), que sí sepamos resolver. Esta es la técnica que se emplea al estudiar el péndulo.

La serie de Taylor de una función en torno a un punto $x 0$ es

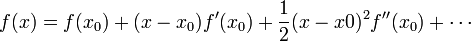
$f(x) = f(x_0) + (x-x_0) f'(x_0) + \frac{1}{2}(x-x0)^2 f''(x_0)+ \cdots$

Aplicando esto a nuestro caso, debemos considerar posiciones próximas a las de equilibrio. Así tenemos

2.4.1 Cerca de x = 0

La fuerza en puntos prósimos al centro será aproximadamente igual

$F(x) = F(0) + (x-0) F'(0) + \cdots \simeq cx$

ya que $F (0) = 0$ por ser una posición de equilibrio (esta es la ventaja de considerar puntos próximos a los de equilibrio). La ecuación de movimiento aproximada será

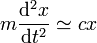
$m\frac{\mathrm{d}^2x}{\mathrm{d}t^2} \simeq cx$

Tenemos ahora dos casos:

Si $c < 0$ , la partícula se comporta como un oscilador armónico. Efectuará oscilaciones con la frecuencia

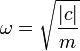
$\omega = \sqrt{\frac{|c|}{m}}$

Se dice que en esta posición, la partícula tiene un punto de equilibrio estable, pues no tiende a alejarse de ella, sino que oscila en sus proximidades.

Si $c > 0$ , la partícula no oscila. Si se aleja un poco de la posición de equilibrio, la fuerza es positiva y tiende a alejarla aun más, y el proceso continúa hasta que la partícula ya está muy alejada, y no vale la aproximación que estamos efectuando. Se dice que la partícula tiene una posición de equilibrio inestable (ya que tiende a alejarse de esta posición de equilibrio. Es como un péndulo que se sostiene verticalmente en su posición superior; a nada que se desvíe de esta posición acaba cayendo.

Si el desarrollo en serie, en lugar de la fuerza lo hacemos en la energía potencial nos queda

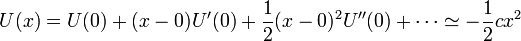
$U(x) = U(0) + (x-0)U'(0) + \frac{1}{2}(x-0)^2 U''(0)+\cdots \simeq -\frac{1}{2}cx^2$

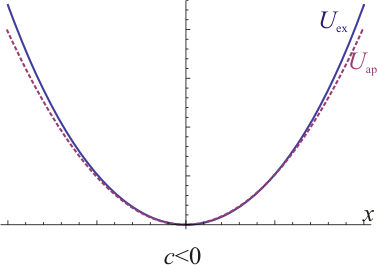
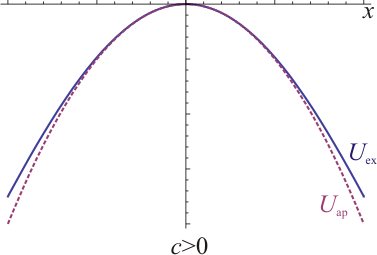
La curva de energía potencial se puede aproximar por una parábola en las proximidades del punto de equilibrio. Cuando el punto de equilibrio es estable, la parábola es hacia arriba, y la partícula se comporta como una bola en un cuenco. Cuando el punto de equilibrio es inestable, la parábola es hacia abajo y la partícula se comporta como una bola en lo alto de una cresta.

2.4.2 Cerca de un mínimo lateral

Supongamos ahora que $c > 0$ y por tanto, además del punto de equilibrio central, hay uno a cada lado. Por simplicidad consideraremos el situado en $x > 0$ . El otro se trata exactamente igual.

Desarrollando la fuerza en serie de Taylor en torno a $x 0 = (c / p) 1 / 2$

$F(x) = F(x_0) + (x-x_0)F'(x_0) +\cdots = -2c\left(x-\sqrt{\frac{c}{p}}\right)$

donde hemos usado que

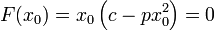
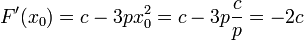
$x_0=\sqrt{\frac{c}{p}}$ $F(x_0)=x_0\left(c-px_0^2\right)=0$ $F'(x_0) = c - 3px_0^2 = c-3p\frac{c}{p}=-2c$

Haciendo $z = x - x 0$ nos queda la ecuación de movimiento aproximada

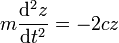
$m\frac{\mathrm{d}^2z}{\mathrm{d}t^2}=-2cz$

que nos dice que la partícula oscila en torno a esta posición de equilibrio con una frecuencia

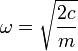
$\omega = \sqrt{\frac{2c}{m}}$

En términos de la energía, si hacemos la aproximación parabólica en torno a esta posición

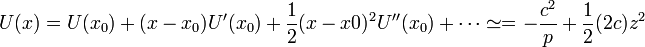
$U(x)=U(x_0)+(x-x_0)U'(x_0)+\frac{1}{2}(x-x0)^2U''(x_0)+\cdots\simeq = -\frac{c^2}{p} + \frac{1}{2}(2c)z^2$

La primera cosstante simplemente nos dice que el mínimo está por debajo de la energía de

x = 0

, pero no añade al movimiento. El segundo término nos dice que la aproximación nos da una parábola hacia arriba y el movimiento es por tanto estable.

Tenemos entonces que para $c > 0$ , el sistema posee un posee un punto de equilibrio inestable (un máximo en la energía potencial) en $x = 0$ , de forma que ahí la curva se aproxima a una parábola hacia abajo. En los dos mínimos situados simétricamente, el punto de equilibrio es estable y la curva se aproxima parábolas hacia arriba.

Oscilador no lineal

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Energía mecánica

2.1.1 Energía potencial

2.1.2 Energía mecánica

2.2 Movimiento periódico

2.3 Puntos de equilibrio

2.4 Pequeñas oscilaciones

2.4.1 Cerca de x = 0

2.4.2 Cerca de un mínimo lateral

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES