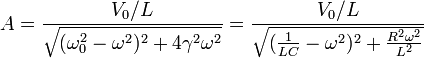Oscilaciones en un circuito

De Laplace

Contenido

1 Enunciado
2 Solución

1 Enunciado

Un circuito formado por una resistencia $R$ , un condensador $C$ y una autoinducción $L$ , asociadas en serie cumple las siguientes ecuaciones para la carga en el condensador y la corriente en el circuito:

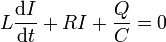
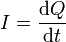
$L\frac{\mathrm{d}I}{\mathrm{d}t}+RI+\frac{Q}{C}=0$ $I =\frac{\mathrm{d}Q}{\mathrm{d}t}$

Suponga en primer lugar que la resistencia es nula ( $R = 0$ ). Pruebe que la carga del condensador oscila armónicamente. ¿Cuál es la frecuencia de oscilación? ¿Qué energía se conserva, análogamente a la energía mecánica de un oscilador armónico?
Si la resistencia no es nula, pruebe que el sistema se comporta como un oscilador amortiguado. ¿Cuál es la resistencia máxima para que haya oscilaciones en el sistema?
Suponga que además de los elementos anteriores, el circuito dispone de una fuente de corriente alterna, que lleva mucho tiempo conectada, de manera que las ecuaciones del circuito son

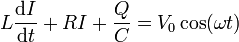
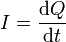
$L\frac{\mathrm{d}I}{\mathrm{d}t}+RI+\frac{Q}{C}=V_0\cos(\omega t)$ $I=\frac{\mathrm{d}Q}{\mathrm{d}t}$

Halle la amplitud de las oscilaciones de la carga del condensador, como función de los parámetros del circuito y de la frecuencia y amplitud del voltaje aplicado.

2 Solución

Aunque a primera vista no lo parezca, la solución de este problema es similar a la de un oscilador mecánico. El truco es buscar una ecuación diferencial que describe el comportamiento de alguna de las magnitudes físicas del problema y que sea formalmente análoga a la del oscilador mecánico. Veamos cada uno de los casos que se plantean

2.1 Resistencia nula

En este caso las ecuaciones diferenciales que describen la carga en el condensador y la corriente que llega hasta él son

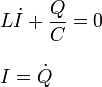
$\begin{array}{l} \displaystyle L\dot{I}+\frac{Q}{C}=0\\ \\ I=\dot{Q} \end{array}$

Para obtener una sola ecuación diferencial derivamos la segunda una vez y sustituimos en la primera. Queda

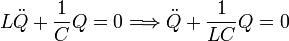
$L\ddot{Q}+\frac{1}{C}Q=0\Longrightarrow \ddot{Q}+\frac{1}{LC}Q=0$

Esta ecuación es similar a la de un oscilador armónico

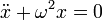
$\ddot{x}+\omega^2x=0$

Por tanto las soluciones serán similares, es decir, una combinación de senos y cosenos con frecuencia angular y período

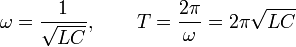
$\begin{array}{lccr} \displaystyle\omega=\frac{1}{\sqrt{LC}},&\,\,\,&\displaystyle T=\frac{2\pi}{\omega}=2\pi\sqrt{LC} \end{array}$

2.1.1 Energía conservada

Para buscar la expresión de la energía que se conserva en el caso del circuito, comparamos las ecuaciones del oscilador mecánico y del circuito

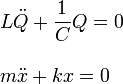
$\begin{array}{l} \displaystyle L\ddot{Q}+\frac{1}{C}Q=0\\ \\ \displaystyle m\ddot{x}+kx=0\\ \end{array}$

En el oscilador mecánico $m$ es la masa y $k$ la constante del muelle. En el circuito, $L$ es la autoinducción y $Q$ la carga eléctrica acumulada en las placas. La comparación de estas dos ecuaciones sugiere la analogía

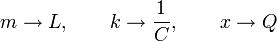
$\begin{array}{lccccr} \displaystyle m\to L,&\,\,\,&\displaystyle k\to\frac{1}{C},&\,\,\,&x\to Q \end{array}$

Si recordamos que en el oscilador mecánico la energía potencial elástica es

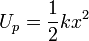
$U_p=\frac{1}{2}kx^2$

la analogía nos lleva a identificar la energía

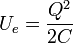
$U_e=\frac{Q^2}{2C}$

Esta es la energía potencial electrostática. Está asociada a la carga eléctrica almacenada en las placas del condensador.

Para buscar el análogo a la energía cinética, establecemos la analogía entre la velocidad y la intensidad de corriente

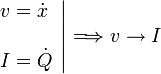
$\left. \begin{array}{l} v=\dot{x}\\ \\ I=\dot{Q} \end{array} \right| \Longrightarrow v\to I$

Así pues, por analogía con la energía cinética llegamos a la energía

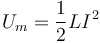
$U_m=\frac{1}{2}LI^2$

Esta es la energía magnética. Está asociada al campo magnético producido por la corriente eléctrica.

En el oscilador mecánico, la energía mecánica es la suma de la potencial elástica y la cinética. En el circuito, definimos una energía total como la suma de la energía potencial electrostática y la magnética

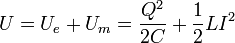
$U=U_e+U_m=\frac{Q^2}{2C}+\frac{1}{2}LI^2$

Al igual que en el caso mecánico, esta energía se conserva. El comportamiento del circuito puede entenderse como un trasvase de ida y vuelta entre la energía eléctrica y la magnética.

2.2 Resistencia no nula

En este caso, al derivar en la ecuación de la corriente y sustituir en la primera obtenemos la ecuación diferencial

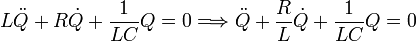
$L\ddot{Q}+R\dot{Q}+\frac{1}{LC}Q=0\Longrightarrow \ddot{Q}+\frac{R}{L}\dot{Q}+\frac{1}{LC}Q=0$

Esta ecuación es análoga a la del oscilador mecánico amortiguado

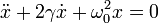
$\ddot{x}+2\gamma\dot{x}+\omega_0^2x=0$

En el caso eléctrico se tiene

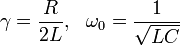
$\gamma=\frac{R}{2L},\,\,\,\,\omega_0=\frac{1}{\sqrt{LC}}$

Por tanto, en el caso eléctrico la carga se comporta siguiendo los regímenes subamortiguado, sobreamortiguado y crítico descritos en el oscilador mecánico.

En el régimen subamortiguado la carga oscila con frecuencia

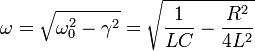
$\omega=\sqrt{\omega_0^2-\gamma^2}=\sqrt{\frac{1}{LC}-\frac{R^2}{4L^2}}$

y la amplitud decae según una exponencial $e - γ t = e - R t / 2 L$ .

El régimen crítico aparece cuando el radicando se anula, es decir, cuando se cumple

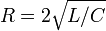
$R=2\sqrt{L/C}$

Para resistencias por encima de este valor el régimen es sobreamortiguado y no se producen oscilaciones.

2.3 Circuito forzado

Este caso es análogo al de un oscilador forzado y amortiguado. En este caso el término forzador corresponde a un generador de corriente alterna que suministra un voltaje oscilante con una frecuencia $ω$ . La ecuación diferencial puede escribirse

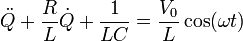
$\ddot{Q}+\frac{R}{L}\dot{Q}+\frac{1}{LC}=\frac{V_0}{L}\cos(\omega t)$

Comparando con la ecuación de un oscilador mecánico forzado,

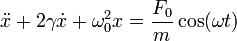
$\ddot{x}+2\gamma\dot{x}+\omega_0^2x=\frac{F_0}{m}\cos(\omega t)$

hacemos las equivalencias

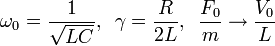
$\omega_0=\frac{1}{\sqrt{LC}},\,\,\,\gamma=\frac{R}{2L},\,\,\,\frac{F_0}{m}\to\frac{V_0}{L}$

El comportamiento que encontramos para el oscilador mecánico usando fasores se puede aplicar a este caso directamente. Así, la carga en el condensador oscila en el tiempo según la expresión

$Q (t) = A cos(ω t + φ)$

La frecuencia de oscilación $ω$ es la que viene impuesta por el generador. El desfase es

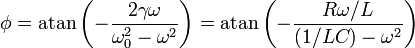
$\phi = \mathrm{atan}\left(-\frac{2\gamma\omega}{\omega_0^2-\omega^2}\right)= \mathrm{atan}\left(-\frac{R\omega/L}{(1/LC)-\omega^2}\right)$

Por su parte, la amplitud de oscilación es

$A=\frac{V_0/L}{\sqrt{(\omega_0^2-\omega^2)^2+4\gamma^2\omega^2}}= \frac{V_0/L}{\sqrt{(\frac{1}{LC}-\omega^2)^2+\frac{R^2\omega^2}{L^2}}}$

Oscilaciones en un circuito

De Laplace

Contenido

1 Enunciado

2 Solución

2.1 Resistencia nula

2.1.1 Energía conservada

2.2 Resistencia no nula

2.3 Circuito forzado

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES