Problemas de dinámica del sólido rígido (GIE)

De Laplace

1 Momento de inercia de un sistema de partículas

Se tiene un sólido formado por ocho partículas de masa m situadas en los vértices de un cubo de arista a. Halle el momento de inercia del cubo respecto a los siguientes ejes:

1. Uno perpendicular a una cara y que pase por el centro del cubo.
2. Uno que pase por dos vértices opuestos.
3. Uno que pase por los centros de dos aristas opuestas.
4. Uno que pase por una arista

2 Sólido formado por tres partículas

Un sólido está formado por tres partículas, una de masa 200 g situada en 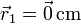y dos de 100 g que se encuentran en 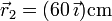y 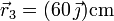, respectivamente. Las velocidades de las masas valen cada una 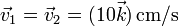y .

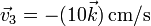1. ¿Cuál es la posición del centro de masas del sistema?
2. ¿Cuánto vale el momento de inercia de este sólido respecto a un eje que pasa por 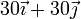(cm) y tiene la dirección del vector ?
3. Si en este sólido se aplica sobre la masa de 200 g una fuerza 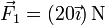y sobre las masas de 100 g una fuerza . ¿Cuánto vale la aceleración del centro de masas del sólido?

3 Cálculo de momentos de inercia

Halle los siguientes momentos de inercia de sólidos de densidad homogénea:

1. Una corona cilíndrica de masa M radio interior R₁ y exterior R₂, con altura h, respecto al eje del cilindro.
2. Una corona esférica de masa M, radio interior R₁ y exterior R₂, con respecto a un eje que pasa por su centro. ¿A qué se reduce el resultado en el caso de una esfera maciza y de una superficie esférica?
3. Una placa cuadrada de masa M y lado b respecto a:
   1. Un eje que pasa por los centros de dos lados opuestos.
   2. Un eje perpendicular a ella y que pasa por el centro.
   3. Un eje que pasa por dos vértices opuestos.
4. Un prisma rectangular de masa M y lados a, b y c, respecto a un eje que pasa por los centros de dos caras opuestas.
5. Un péndulo compuesto formado por una barra de longitud H y masa M₁ y un disco de radio R y masa M₂ clavado en un extremo de la barra respecto a un eje perpendicular al plano del disco y que pasa por el otro extremo de la barra.

4 Equilibrio de una barra apoyada

Supongamos que tenemos una barra de masa M y longitud H apoyada en el suelo y en una pared vertical.

1. Suponga primero que no hay rozamiento con las superficies y que la barra forma un ángulo θ con la vertical. ¿Puede quedarse en equilibrio la barra para algún valor de θ?
2. Suponga ahora que la barra posee un coeficiente de rozamiento estático μ con el suelo. ¿Para qué ángulos puede alcanzarse entonces el equilibrio?

5 Movimiento de una barra apoyada

En el mismo sistema del problema anterior, considerése el caso en que no hay rozamiento ni con la pared ni con el suelo. Si la barra se encuentra inicialmente en la posición vertical y por una pequeña perturbación comienza a deslizarse resbalando por el suelo y la pared, ¿llega a separarse en algún momento de la pared? ¿Para qué ángulo?

6 Dos partículas unidas por una barra

Supongamos dos masas iguales unidas por una barra rígida, sin masa. Las masas reposan sobre un plano, sobre el que pueden moverse sin rozamiento. A una de las masas se le comunica una velocidad inicial v₀ perpendicular a la línea de la barra. ¿Cómo es el movimiento siguiente de la barra?

7 Fuerza sobre una barra

Sobre una barra de longitud H y masa M situada en reposo horizontalmente en una superficie sin rozamiento se aplica una fuerza F₀ también horizontal. El punto de la aplicación se encuentra a una distancia b del centro de la barra.

1. Si la fuerza es perpendicular a la barra, ¿cuánto valen la aceleración del CM y la aceleración angular de la barra? ¿Alrededor de qué punto comienza a girar la barra?
2. Suponga ahora que la fuerza forma un ángulo θ con la barra, ¿cuánto valen ese caso las aceleraciones y donde se encuentra el centro instantáneo de rotación?
3. Suponga que la barra se encuentra articulada en un extremo de forma que sólo puede girar en torno a este punto. ¿Cuánto valen las aceleraciones en ese caso? ¿Cuánto vale la fuerza que el punto de articulación ejerce sobre la barra?
4. Si la barra estuviera empotrada en su extremo, de forma que no pudiera moverse de ninguna manera, ¿cuánto vale la fuerza y el momento de reacción ejercidos por la articulación?

8 Péndulo compuesto

Se tiene un péndulo compuesto consistente en una barra de longitud H y masa M suspendida por un punto situado a una distancia b del centro de la barra (b < H / 2). Suponiendo que la barra se desvía un ángulo pequeño θ₀ respecto de la vertical y a partir de ahí se suelta:

1. Determine el periodo de oscilación de la barra
2. Calcule la fuerza ejercida sobre el punto de anclaje cuando la barra pasa por la vertical en su oscilación.

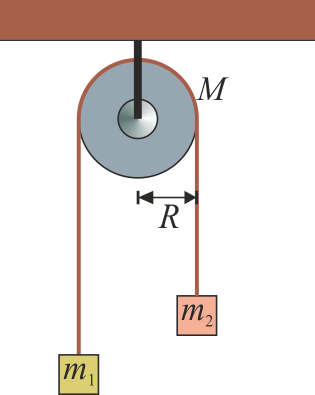
9 Máquina de Atwood con polea pesada

Dos masas m₁ y m₂ están unidas por una cuerda ideal, inextensible y sin masa. Esta cuerda pasa por una polea de masa M, que se puede modelar como un cilindro de radio R. La polea no tiene rozamiento que le impida girar en torno a su eje. Determine la aceleración con la que se mueven las masas, las tensiones en cada tramo de la cuerda, así como la fuerza en el punto de anclaje de la polea.

10 Rotación de un patinador

Un patinador sobre hielo, que pesa 70 kg y mide 180 cm gira uniformemente con sus brazos pegados verticalmente a su cuerpo, con un periodo de 1 s por vuelta. Si ahora levanta sus brazos y los extiende completamente, ¿cuál será su nuevo periodo de rotación? Haga una estimación del resultado, justificando las aproximaciones efectuadas.

Estime igualmente el trabajo necesario para efectuar esta maniobra.

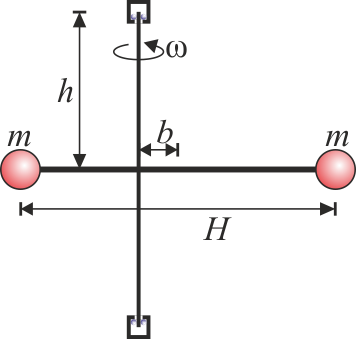
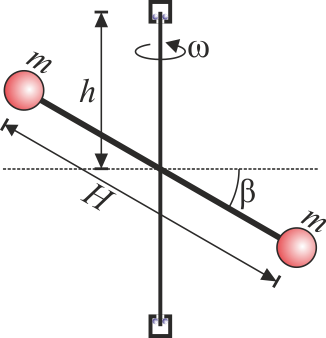
11 Rotores desequilibrados

Se tiene un rotor formado por dos masas iguales, de valor m situadas en los extremos de una barra ideal (sin masa) de longitud H. Cuando este rotor está equilibrado gira en torno a un eje perpendicular a la barra y que pasa por su centro. Este eje está anclado en dos rodamientos situados a una distancia h del centro de la barra (uno por encima y otro por debajo de ella).

Calcule las fuerzas horizontales que el rotor produce sobre los rodamientos cuando gira con velocidad angular constante ω en torno al eje si:

1. Es horizontal pero se encuentra descentrado de forma que el eje no pasa por el centro de la barra, sino a una distancia b de éste.
2. Está centrado pero la barra está inclinada respecto a la horizontal un ángulo β

Desprecie el efecto del peso.

        

12 Rodadura por una pendiente

En lo alto de un plano inclinado de altura 1.2 m y con una pendiente del 75% se encuentran los siguientes objetos, todos ellos de masa 0.5 kg y radio 10 cm:

• Una superficie cilíndrica hueca
• Un cilindro macizo
• Una superficie esférica hueca
• Una esfera maciza

Si se sueltan a la vez desde el extremo superior del plano, ¿con qué velocidad llega cada uno al punto más bajo del plano? ¿en qué orden llegarán y cuanto tarda cada uno en llegar? Si además se suelta un bloque de 0.5 kg que desliza sin rozamiento por el plano, ¿llegará antes o después que los objetos rodantes? ¿Cuánto?

13 Vuelco en un plano inclinado

Se tiene un bloque en forma de prisma de altura h y base cuadrada de lado b, situado sobre un plano inclinado un ángulo β. Dos de los lados de la base son paralelos a la dirección de descenso del plano (y los otros dos son ortogonales). El coeficiente de rozamiento (estático y dinámico) entre el bloque y el plano vale μ.

Determine el máximo valor de h para que el bloque no vuelque si

1. El coeficiente de rozamiento μ > tg(β).
2. El coeficiente de rozamiento μ < tg(β).

14 Vuelco de un camión

Un camión de mudanzas va cargado de forma que su centro de gravedad se encuentra a 3 m del suelo. Si la distancia entre ruedas del camión es de 2.40 m, ¿cuál es la máxima velocidad con la que puede tomar una rotonda de 20 m de radio sin volcar?

15 Dimensiones del Mundo Anillo

En la novela de Larry Niven Mundo Anillo se describe un mundo artificial consistente en un anillo sólido que gira en torno a una estrella similar al Sol. El Mundo Anillo tiene un radio de 153 Gm y la gravedad aparente en su superficie interior es de 9.73 m/s². La anchura del anillo es de 1.60 Gm. El material de que está hecho (denominado scrith) tiene un espesor medio de 30 m siendo la masa total del Mundo Anillo 2.1×10²⁷kg. Con esta información, determine:

1. La velocidad angular del mundo anillo.
2. Su periodo orbital.
3. La velocidad lineal de su superficie.
4. Su momento de inercia.
5. Su momento cinético.
6. Su energía cinética.
7. La densidad de masa del scrith.